OSCILLATIONS Physical and mathematical treatment of undamped simple harmomc motion.

SIMPLE HARMONIC MOTION

A particle is said to be moving in simple harmonic motion if its acceleration is always directed towards a fixed point and is proportional to its displacement from that point. In mathmatical terms a = -k x, where a is acceleration, x is the displacement from its equilibrium position and k is a positive constant. We use w² for the constant, so this becomes

a = -w² x From this we integrate to get the velocity.
Rewriting a as v ^dv/_dx
we inegrate (the lower limit A being the maximum displacement ) ₀^v v dv = _A^v -w² x dx
v² = w² (A² - x²) This is further inegrated to give x = A sin( w t ) when t (time) is taken to be zero when the particle is at the equilibrium position (x = 0), if the time is started at a different time then the equation is x = A sin( w t + E), where E is the phase difference, this is equal to 2 π when t = 0 at maximum displacement x = A. A, the maximum displacement is known as the amplitude of the oscillation. It should be noted that when x = A sin ( w t ) is substited into the velocity equation we get another equation for v, v = A w cos( w t )

PERIOD AND FREQUENCY
The Period of the oscillation is the time taken for the particle to go through one cycle and come back to the state that it was in (Note that except at the extreme displacements this means the 2nd time it passes through the point. The frequency is the number of oscillations made per second and is hence the inverse (1 divided by) the period. In simple harmonic motion, there is a constant period and frequency, this depends on the value of w. w is the angular frequency and is equal to 2 &pi mulitplied by the frequency.

GRAPHICAL EXAMINATION

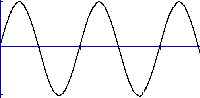
displacement Displacement with time - If we take t = 0 when the particle is moving through the equilibrium position in the +ve direction, then the subsequent displacement of a partilce is described by a A sin( w t ), hence it is periodic and repeats itself every ^{2 &pi} / _w seconds. There are two and a half cylces on the graph. As acceleration is directly proportional to displacement it follows the same pattern.

time

velocity Velocity with time - For the same assumption as the previous graph the velocity varies with time periodically with the same period. But is ^&pi /₂ out of phase, such that maximum velocity ( w A) occurs at displacement = 0.

time

Please tell me about any mistakes on this page, or urls relevent to it. Thank you.
Rob Coles 05 May 1996 11:56:40

displacement		Displacement with time - If we take t = 0 when the particle is moving through the equilibrium position in the +ve direction, then the subsequent displacement of a partilce is described by a A sin( w t ), hence it is periodic and repeats itself every ^{2 &pi} / _w seconds. There are two and a half cylces on the graph. As acceleration is directly proportional to displacement it follows the same pattern.
	time

velocity		Velocity with time - For the same assumption as the previous graph the velocity varies with time periodically with the same period. But is ^&pi /₂ out of phase, such that maximum velocity ( w A) occurs at displacement = 0.
	time