2.3 Allgemeine Einflüsse auf Genauigkeit und Auflösung
 

nach [22] [23] [24]

Unweigerlich ist jedes Messresultat mit einem gewissen Fehler behaftet, der sich aus einem systematischen und einem zufälligen Fehler zusammensetzt. Diese Differenzierung ist sinnvoll, will man das erhaltene Messergebnis verstehen.

Der systematische Fehler ist ein regelmässiger Fehler (Unvollkommenheit des Messverfahrens oder des Messgerätes), der erkennbar ist, wenn sämtliche Messumstände (ein anderes Messverfahren) ändern. Dieser Fehler kann vermieden werden, indem man die Messwerte berichtigt. Demnach lassen sich systematische Fehler durch blosse Wiederholungen von Messungen weder erkennen noch ausschalten.

Der zufällige Fehler ist im einzelnen nicht gesetztmässig erfassbar und kann deshalb nicht vermieden werden. Obgleich die Ursache (etwa die zeitliche Änderung der Messbedingungen) häufig bekannt ist, ist es nicht möglich, das Ausmass der Wirkung zu bestimmen. Wiederholt man eine Messung jedoch mehrmals, so wird eine Streuung der Messwerte beobachtet, die eine statistische Auswertung zulässt. Auf diese Weise kann der zufällige Fehler minimiert werden.

Der Messtechnik ist somit eine obere Grenze für die Genauigkeit^xiii und Auflösung^xiv vorgegeben.Trotzdem kann durch die geeignete Wahl von Messparametern die Genauigkeit gesteigert werden. Im folgenden wird nur auf einzelne Aspekte eingegangen. Dabei wird einfachheitshalber nur der zufällige Fehler betrachtet, auf den sich die Gesetzte der Fehlerfortpflanzung anwenden lassen, die auf dem Gaussschen Ausgleichsprinzip der kleinsten Quadratsumme beruhen.
 

nach [1 ii)]

Die Genauigkeit einer Zeitmessung wird durch die Eindeutigkeit des Signalpegels bestimmt. Nun ist es einmal so, dass einem empfangenen Signal immer ein Rauschen (ein zufälliger Fehler) überlagert ist, daher ist es nicht möglich, einen absoluten Zeitpunkt zu bestimmen. Mit folgender Beziehung kann jedoch die minimal erreichbare Genauigkeit s_t berechnet werden.

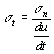 (2-2)

Die Ableitung des Signals nach der Zeit ^du/_dt, die ungefähr dem Verhältnis der Signalamplitude zur Anstiegszeit entspricht, muss möglichst gross, und das Signalrauschen s _n muss möglichst klein sein, um die Abweichung der Zeitbestimmung s _t zu minimieren. Je grösser also die Frequenz, oder je kleiner die Pulsbreite eines Signals ist, desto genauere Messergebnisse können erreicht werden.