Sarà Vero?????

La teoria della Ristretta o Speciale Relatività fu pubblicata da Einstein nel 1905 in una memoria intitolata "Sulla elettrodinamica dei corpi in movimento".

In quell' articolo scrisse: "[...] nessuna caratteristica dei fatti osservati corrisponde al concetto di un etere assoluto; [...] per tutti i sistemi di coordinate per i quali valgono le equazioni della meccanica, valgono anche le equivalenti equazioni dell'elettrodinamica e dell'ottica [...]. In quanto segue facciamo questa ipotesi e introduciamo l'ulteriore postulato, un postulato a prima vista inconciliabile colle ipotesi precedenti, che la luce si propaga nello spazio vuoto con una velocità c che è indipendente dalla natura del moto del corpo che la emette. Queste due ipotesi sono del tutto sufficienti a darci una semplice e consistente  teoria dell'elettrodinamica dei corpi in movimento basata sulla teoria di Maxwell per i corpi in riposo".

La teoria di Einstein è basata dunque su due postulati fondamentali:

1.     Le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali. Non esiste un sistema inerziale privilegiato (Principio di relatività).

2.     La velocità della luce nel vuoto ha lo stesso valore c in tutti i sistemi inerziali (Principio della costanza della velocità della luce).

Con soli questi due postulati Einstein rivoluzionò il mondo fisico. Si deriva direttamente dai due principi suddetti e comprendono le trasformazioni di Galileo, come caso particolare, quando la velocità v del sistema è molto minore della velocità c.

Possono considerarsi sei le conseguenze fondamentali della teoria della relatività ristretta:

1.     Velocità limite c dei corpi

2.     Relativizzazione del concetto di simultaneità

3.     Dilatazione dei tempi

4.     Contrazione delle lunghezze

5.     Variazione della massa di un corpo quando la velocità dello stesso è confrontabile con quella della luce

6.     Nuova equazione per l'energia cinetica detta equazione relativistica per l'energia

    Velocità limite c dei corpi

Analizzando le leggi della fisica classica si nota che esse non impongono nessuna limitazione all'intensità del vettore velocità di un corpo.

Possiamo così ipotizzare, ad esempio, l'esistenza di un'onda che viaggi a velocità v infinita.

Tale onda sarebbe quindi in grado di attraversare tutte le parti del nostro universo in un tempo nullo. Risulta evidente (e quasi logico) che tale realtà non è attualmente realistica ed inoltre nessun esperimento ha mai confermato tale ipotesi.

Nelle equazioni relativistiche è presente il cosiddetto fattore relativistico

Esso impone che il vettore velocità v abbia una intensità non maggiore di c poiché se così fosse β rappresenterebbe la radice di un numero negativo e questa cosa non è algebricamente accettabile poiché non si definiscono, in R, radici di numeri negativi.

La velocità limite per il moto di qualunque oggetto naturale è  c.

Operando infatti la somma vettoriale di velocità secondo i criteri della fisica classica si ha

V=v₁+v₂

Mentre Einstein adopera un fattore di correzione

V=(v₁+v₂)/(1+v₁v₂/c²)                       v₁<<c; v₂<<c

Da tale formula, per il caso di velocità prossime a quella della luce risulta che

V=c

Ciò dimostra quanto sopra affermato.

Relativizzazione del concetto di simultaneità

Eventi che sono simultanei in un particolare sistema di riferimento possono cessare di esserlo se la misura avviene rispetto a un diverso sistema di riferimento inerziale.

Per la dimostrazione consideriamo i sistemi di riferimento inerziali O ed O', l’uno in moto rispetto all’altro con velocità v nella direzione e nel verso dell’asse x ( fig. 1 ).

Sfruttiamo un esperimento concettuale (cioè un sperimento che non può essere effettivamente eseguito, ma immaginabile)

Possiamo immaginare che due petardi, posti nei punti A e B dell’asse x di O siano fatti esplodere a distanza da uno stesso comando, situato nel punto medio R fra A e B. Per misurare la simultaneità di questi eventi, abbiamo dotato il sistema di riferimento di un rilevatore di luce posto in R per verificare se, effettivamente, i due lampi di luce prodotti dagli scoppi arrivano contemporaneamente in R. Ma gli stessi due eventi visti dall’osservatore in O', non sono più simultanei.

Ciò dimostra che la simultaneità cessa di essere un concetto assoluto.

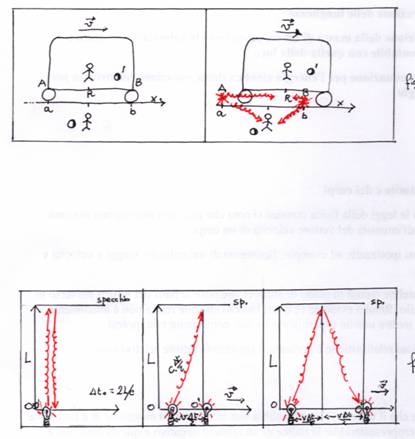fig. 1    e      fig.  2

Dilatazione dei tempi

La conseguenza però più strabiliante è questa: un orologio va al ritmo più veloce quando è a riposo rispetto all'osservatore. Quando si muove con velocità v rispetto all'osservatore, il suo ritmo misurato subisce un rallentamento di un fattore γ

Per la dimostrazione consideriamo ancora una volta i sistemi di riferimento O ed O' ed un orologio a impulsi luminosi situato in una posizione fissa nel riferimento O'     (fig.  2 ).

Per un osservatore solidale con il sistema di riferimento O, il tempo misurato attraverso un tic-tac dell’orologio sarà

Dt₀=2L/c

Dove con L si intende la distanza tra i due specchi.

Supponendo che O' sia in moto con velocità costante v rispetto a O, costui trova il percorso dell’orologio luminoso del sistema O più lungo.

Indicando con Dt l’intervallo di tempo necessario all’impulso luminoso per percorrere i due lati obliqui del triangolo isoscele, applicando il teorema di Pitagora a uno dei due triangoli rettangoli che lo formano otteniamo:

c²Dt²/4=v²Dt²/4+L²

con Dt= intervallo di tempo misurato dall’osservatore in O.

Dal punto di vista di O dunque l’orologio in moto scandisce il tempo con un ritmo più lento del suo.

Dalla precedente equazione si ottiene 

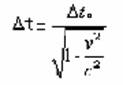
;     posto    γ = 1/ √ 1 – (v/c)2      è  ∆t = γ  ∆t0

Dato che                                                                                                              

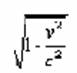
è minore di uno ne segue

∆t > ∆t0

Per l'osservatore solidale con O' il tempo si è dilatato!

               Contrazione delle lunghezze

Un'altra conseguenza, che cozza con il nostro senso comune, è questa: la lunghezza di un corpo è più grande quando questo è a risposo relativamente all'osservatore. Quando il corpo si muove con una velocità v rispetto all'osservatore la sua lunghezza si contrae, nella direzione del moto, del fattore  β.

Vediamo di dimostrare quanto affermato attraverso un procedimento algebrico.

In base alla teoria del moto rettilineo uniforme sappiamo che

S=vt

Analogamente

Dx=vt₀  (lunghezza misurata da un osservatore

solidale con il sistema di riferimento)

Dx₀=vt  (lunghezza misurata da un osservatore da un

sistema di riferimento in moto rispetto a quello considerato)

Dividendo membro a membro ed otteniamo

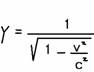
Dx/Dx₀=vt₀/vt         Þ

essendo t=g t₀

con

(y>1)

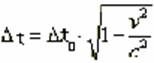
Dx/Dx₀=vt₀/vt₀g   Þ  Dx=Dx₀/g  Þ

cioè Dx<Dx₀

Abbiamo così dimostrato quanto in precedenza affermato.

Variazione della massa di un corpo quando la velocità dello stesso è confrontabile con quella della luce

Intuitivamente possiamo iniziare la nostra analisi considerando le leggi classiche di un moto uniformemente accelerato della dinamica in base alle quali

⁽¹⁾   

Risulta però evidente che scelta una accelerazione a possiamo far trascorrere un tempo tanto lungo da rendere v maggiore di c e questa ipotesi non è accettabile poiché, come già visto, nessun corpo può viaggiare più veloce della luce.

In base al secondo principio di Newton sappiamo che

di conseguenza, con una semplice sostituzione, la (1) diventa

A questo punto, essendo a costante anche F  sarà costante, quindi sarà l'aumento della massa m che permette al vettore v di non avere una intensità maggiore di c.

L'equazione che esprime la variazione della massa di un corpo è la seguente

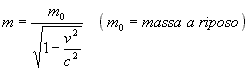cioè  misurata da un osservatore "a  riposo"   rispetto al corpo

Nuova equazione per l'energia cinetica detta equazione relativistica per l'energia

Analizziamo ora una delle equazioni più famose e ricordate della fisica moderna

Questa, che prende il nome di Equazione relativistica per l'energia, rappresenta una nuova legge per l'energia cinetica di una particella che si muove con velocità v.

Sviluppando l'equazione otteniamo

⁽¹⁾    

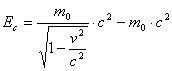
L'espressione risulta così costituita da due termini. Il primo dipende dalla velocità v del corpo mentre il secondo è indipendente da essa e pertanto prende il nome di energia di riposo o di quiete.

    Questa legge sembra discostarsi molto dalla classica equazione per l'energia cinetica ma in realtà, quando v è molto minore di c, le due equazioni si assomigliano. Attraverso un processo matematico ricaviamo la seguente approssimazione per g:

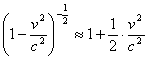
 Con una semplice sostituzione nella (1) otteniamo l'equazione classica per l'energia cinetica

    L'identificazione del termine

come energia di riposo non è solo una convenzione. Gli studi e gli esperimenti odierni hanno mostrato che la conversione dell'energia di riposo in energia cinetica, con una corrispondente perdita di massa, è un fenomeno che si verifica comunemente e continuamente nel decadimento radioattivo e nelle reazioni nucleari.

    Tale scoperta determinò l'inizio del periodo nucleare e furono proprio gli studi svolti dallo scienziato Albert Einstein, in America, che permisero la realizzazione delle prime bombe nucleari che furono utilizzate dagli stessi americani per determinare le sorti del secondo conflitto mondiale.