Diffraction

Diffraction describes the process whereby light bends around the edges of an obstacle. It is a phenomenon that is characteristic of wavemotion and is also observed with waves on the surface of water or sound waves, but it is usually less noticeable in the case of light. The diagram below shows a light wave approaching from the left towards a small aperture, or hole, in a barrier. The blue vertical lines indicate the form of the wavefront - they could be considered to be lines that run across the crests of the waves. Upon passing through the aperture, the wave begins to spread around the edges into the region that one might expect to be shadow.
$diffraction$

The diffracted wave to the right of the barrier is not uniform in intensity. For a circular aperture, the intensity distribution is indicated by the diffraction pattern on the right of the diagram. The most intense part of the transmitted beam is on the central axis passing through the aperture but this is surrounded by a number of concentric rings that are separated by intensity minima. These minima arise as a consequence of destructive interference between waves from different points in the plane of the aperture.

The effects of diffraction are most noticeable when the aperture diameter is a small multiple of the wavelength of light. In such cases, the angle between the direction of the central axis and the first minimum is relatively large. For apertures that are several centimetres across, the effects of diffraction on a light beam are very small, but diffraction still occurs and it can have important consequences concerning such matters as the resolution of optical instruments. The aperture need not necessarily be a hole in a barrier as described above. It could be a lens through which a beam of light passes or a mirror from which a beam is reflected. In general, the aperture is anything that limits the width of the beam. The effects of diffraction are particularly important in laser diodes because of the small dimensions of the laser light source.

The mathematical treatment of diffraction from a circular aperture is complex but a useful result is given below.

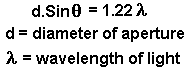
From this expression, it can be seen that the angle at which the first minimum in intensity occurs increases as the wavelength increases or the diameter of the aperture is reduced.