Orientation of Last Layer Corners
Before I start talking about how I solve the last layer, an
introduction to my notation is in order. Megaminx notation isn't
standard by any means, but here's what I use:
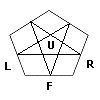
Twists are denoted by F+, R-, etc. Double turns simply use ++ or -- to
their direction. So R+ F-- is a single clockwise twist of R followed by
a double anticlockwise twist of F. I don't worry about the other faces because none of my sequences use them.
My method for orienting the corners of the last layer uses exclusively
what may be the most well-known cube algorithm ever, the Sune.
The algorithm is the same on the cube and Megaminx: R+ U+ R- U+ R+ U-- R-
However, I do need to point out one crucial difference. On a cube, the
Sune does not change the permutation of the corners at all. On a
Megaminx, it does. So the actual cases work out a bit differently, but
it's still all very easy to learn.
You'll need to know this sequence and the AntiSune, it's inverse, and
their mirrors. Also note that when I say "Double Sune" I simply mean
two Sunes one after the other, which "blend" into each other, ie, U--
R- R+ U+ becomes just a single U-. Basically the idea of this method is
to apply Sunes and AntiSunes in different places to reach the solved
position in 2-3 short algorithms than to memorize several longer
algorithms to directly solve each case. It's much easier to learn a new
place to use an algorithm you already know than to learn a new
algorithm entirely. This is especially true on the Megaminx where there
are many more cases than the cube.
I've grouped the cases into three groups to organize them and suggest
some sort of learning order. In all of the diagrams the pictures have
been drawn so that the neccesary Sune or AntiSune will always start
with R+.
Group 1 - Basic Cases
These are the cases you need to know to solve the puzzle. These cases may come up mirrored.
Case 1A - Solved Case, included here for completeness
Case 1B - Solved by Sune
Case 1C - Solved by AntiSune

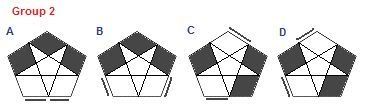
Group 2 - Three Corner Cases
These cases all deal with three corners correct. They are all symmetrical, the mirrors are the same.
Case 2A - Sune gives Case 1B
Case 2B - AntiSune gives Case 1B
Case 2C - Sune gives Case 1B
Case 2D - AntiSune gives Case 1C
Group 3 - The Rest
These cases all deal with one or zero corners correct. These aren't
needed to learn immediately, because if you don't know what to do you
can just do a Sune and land somewhere in groups one or two. Learning
this eliminates the unlucky times when you might have to use three
algorithms. It's important to be able to recognize the mirrors!
Group 3 in "under construction", so-to-speak.
Don't forget navigation links later!


