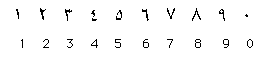Part III. Mathematics Advancements by Muslims:

Introduction: Just as with science, the Muslims learned from the Greeks, Egyptians, Indians, and Babylonians. Many translations took place in the House of Wisdom in Baghdad, the capital of the Abbasid Empire. The Muslim scholars there translated the works of the Greeks who loved mathematics and geometry, including Euclid's work on geometry. They borrowed from India a number system that had a zero and rewrote it as their own. They borrowed from the Babylonians whose number system was based on 60 (just like the minutes in an hour), and from the ancient Egyptians who had the math and geometry skills to build incredible pyramids. So from the beginning, "Arabic math" was a mixing of international knowledge. But the Muslims made additional contributions of their own, and through their study and written work, they preserved the knowledge of mathematics that otherwise might have been lost to the world.

A. Arabic Numerals

One of the greatest advances was the introduction of "Arabic" numerals. The "Arabic" numerals were influenced by India's mathematics. It is a system based on place values and a decimal system of tens. This system had a zero to hold a place. These numbers were much easier to use for calculation than the Roman system which used numbers, like I, V, X, L, C, M, etc. Addition, subtraction, multiplication and division now became easy.

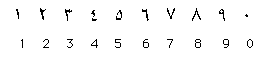
Top: Western Arabic or Hindu-Arabic Numerals

Below: Modern Arabic numerals which developed from them

With Arabic numerals, simple fractions and decimal fractions were also possible. Fractions and decimal fractions were also described by Muslim mathematicians during the Middle Ages.

B. The Development of Algebra.

Al Khwarizmi wrote the first book on algebra. (The name "algebra" was first used by him.)

Al Khwarizmi was born about 790 in Baghdad (now in Iraq) and died about 850.

The word for "Algebra" comes from the Arabic word for "al-jabr" which means "restoration of balance" in both sides of an equation.. Algebra was based on previous work from Greeks, Alexandrians in Egypt, and Hindus who had preserved the work from ancient Egyptians and Babylonians.

In the ninth century, al-Khwarizmi wrote one of the first Arabic algebras with both proofs and examples. Because of his work, he is called "the Father of Algebra." Al-Khwarizmi was a Persian born in the eighth century. He converted (changed) Babylonian and Hindu numerals into a workable system that almost anyone could use. He gave the name to his math as "al-jabr" which we know as "algebra".

A Latin translation of al-Khwarizmi's book on algebra appeared in Europe in the 12th century. In the early 13th century the new algebra appeared in the writings of the famous Italian mathematician, Leonardo Fibonacci. So, algebra was brought into Europe from ancient Babylon, Egypt and India by the Arabs and then into Italy.

C. Geometry

The scholars at the House of Wisdom in Baghdad and at universities in Cairo, Egypt also contributed to geometry. Geometry was highly developed by the Greeks, and the Muslims translated such great Greek thinkers as Euclid. Muslims used their understanding of geometry into designing wheels of all kinds, especially waterwheels and other systems for drawing up water, in improving farming equipment, and in designing devices of war such as catapults and crossbows. Geometry was also put to work in art, with beautiful geometric designs. Muslims further defined Euclidian geometry, and pointed the way toward the discovery of independent, non-Euclidean geometry developed in the most recent centuries.

D. Trigonometry is also mostly a Muslim creation. It is a branch of mathematics which studies plane and spherical triangles. It developed from the need of astronomers to map points in the sky on a heavenly sphere. Trigonometry's functions, involving ratios such as sine and cosine, tangent and cotangent, were greatly developed and refined in the Islamic lands.

E. Famous Muslim Mathematicians of the Middle Ages

1. Al-Khwarizmi (770 - 840 C.E.) was one of the greatest mathematicians who ever lived and is called the "Father of Algebra". He also helped to bring "Arabic numerals" into use into the Islamic Empire, as well as later into Europe. He also demonstrated operations with fractions for the first time. Khwarizmi influenced the growth of science and mathematics. Several of his books were translated into many other languages, and were used as university textbooks until the 16th century. His approach was systematic and logical. He brought together the knowledge of his time on various branches of science, especially mathematics, and also added his original contributions.

2. Omar Khayyam (1044 - 1123 C.E.): Another great Muslim mathematician was Omar Khayyam. He is best known today for his poetry, but his contribution to mathematics was great. He showed how to express roots of cubic equations by line segments obtained by intersecting conic sections. Khayyam was an outstanding poet, mathematician, and astronomer. His work on algebra was known throughout Europe in the Middle Ages, and he also contributed to a calendar reform. Khayyam refers in his algebra book to Pascal's triangle. The algebra of Khayyam is geometrical, solving linear and quadratic equations by methods appearing in Euclid's Elements. Khayyam also gave important results on ratios giving a new definition and extending Euclid's work to include the multiplication of ratios. He poses the question of whether a ratio can be regarded as a number but leaves the question unanswered.

3. Al-Khashi was born in 1390 in Kashan, Iran and died in 1450 in Samarkand (now Uzbek). He calculated 1 (pi) to 16 decimal places which was the best until about 1700. He considered himself the inventor of decimal fractions. He wrote The Reckoners' Key which summarizes arithmetic and contains work on algebra and geometry.

4. Al-Biruni (973 - 1048 C.E.) was a philosopher, astronomer, pharmacologist (one who studies drugs and herbs used for health), botanist (one who studies plants), geologist and mathematician. He translated Euclid's work into Sanskrit (an Indian language), and calculated the earth's circumference (distance around the earth) and radius (distance to the center) with an accuracy that is close to today's measurements.

5. Nasir Al-Din Al-Tusi (1201 - 1274 C.E.) pioneered spherical trigonometry which includes six fundamental formulas for the solution of spherical right-angled triangles. One of his most important mathematical contributions was the treatment of trigonometry as a new mathematical discipline. He wrote on binomial coefficients which Pascal later introduced. (He can be called the "Father of Trigonometry".) He was also an astronomer philosopher, and medical scholar as well as a mathematician.

 

back to tazkirah