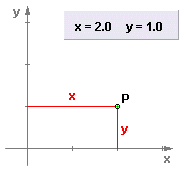
En
la figura de la izquierda aparece representado el punto P
(2,1).
Se escribe primero
la
coordenada x y después la
coordenada y,
separadas por una coma.
¿Qué
es el movimiento?
Estamos
rodeados de cosas que se mueven.
Cinemática y dinámica
Cuando
estudiamos el movimiento de un cuerpo, puede interesarnos solamente conocer cómo
es o puede interesarnos saber por qué
tiene las
características que observamos en él.
La
Cinemática se ocupa de describir los
movimientos y determinar cuáles son sus características mientras que la Dinámica
estudia las relaciones que existen entre las fuerzas y las alteraciones que éstas
provocan en el movimiento de los cuerpos.
La
Posición
Si hemos acordado llamar movimiento al cambio de la posición con el tiempo, será necesario establecer un criterio para determinar qué posición ocupa un cuerpo en un instante. Se trata, de nuevo, de establecer un sistema de referencia adecuado para lo que necesitamos estudiar.
Una dimensión
Imagina que tenemos un cuerpo que se mueve por una recta, es decir que realiza un movimiento en una dimensión. Para determinar su posición sólo necesitamos indicar a qué distancia del origen se encuentra, la posición del cuerpo puede ser positiva o negativa según se encuentre a la derecha o a la izquierda del orígen respectivamente.
Dos dimensiones
Si
el cuerpo realiza un movimiento en dos dimensiones, es decir se mueve por un
plano, necesitaremos dos coordenadas para determinar la posición que ocupa en
un instante dado.
Los
dos valores que determinan la posición de un cuerpo en un plano podemos
establecerlos utilizando como referencia un sistema de coordenadas
cartesianas o un sistema de coordenadas polares.
En
el caso de las coordenadas cartesianas se utilizan las distancias a los dos ejes
acompañadas de los signos (+)
ó
(-).
|
|
En
la figura de la izquierda aparece representado el punto P
(2,1).
Se escribe primero
la
coordenada x y después la
coordenada y,
separadas por una coma. |
El
signo negativo para la coordenada x se utiliza
si el punto se encuentra a la izquierda del orígen
y para la coordenada y cuando está por debajo del orígen.
Las
coordenadas polares utilizan la longitud de la recta que une nuestro punto con
el punto de referencia y el ángulo que forma esta recta con la horizontal.
|
|
En
la figura de la izquierda se representa el punto P(2,40°) lo que
significa que la distancia r vale 2
y que el ángulo vale 40° |
Tres dimensiones
En
el caso de un cuerpo que siguiera una trayectoria de tres
dimensiones, es decir que se moviera por un espacio, necesitaríamos tres
coordenadas para determinar su posición en un instante dado.
El tiempo es la cuarta dimensión
Como
el movimiento es el cambio de la posición con el tiempo, además de conocer la
posición, nos interesa saber el instante en el que el cuerpo ocupa dicha posición.
Si
representamos el conjunto de las diferentes posiciones que ocupa un móvil a lo
largo del tiempo, obtenemos un línea llamada trayectoria.
Vector
de Posición
Si
sabemos cómo se determina la posición
de un punto, es muy fácil entender qué es un vector de posición.
Trayectoria
La
trayectoria es la línea formada por las sucesivas posiciones por las que pasa
un móvil.
|
Tipos
de Movimientos |
Tipos
de trayectorias
|
|
de
una dimensión |
Líneas
rectas |
|
de
dos dimensiones |
Líneas
curvas planas |
|
de
tres dimensiones |
Líneas
curvas no planas |
Movimientos rectilíneos
Podemos
decir que son los movimientos cuya trayectoria es una línea
recta.
Movimientos curvilíneos
Podemos distinguir entre dos tipos de
movimientos curvilíneos: los de dos dimensiones y los de tres dimensiones.
Así,
podemos citar:
1.
Movimientos
circulares
2.
Movimientos
elípticos
3.
Movimientos
parabólicos
4.
Etc
Distancia
y Desplazamiento
En
el lenguaje ordinario los términos distancia y desplazamiento se utilizan como
sinónimos, aunque en realidad tienen un significado diferente.
La
distancia recorrida por un móvil es la longitud de su trayectoria y se trata de
una magnitud escalar.
|
|
El desplazamiento efectuado es una magnitud
vectorial. El vector que representa al desplazamiento tiene su orígen
en la posición inicial, su extremo en la posición final y su módulo
es la distancia en línea recta entre la posición inicial y la final. |
|
|
El final del recorrido coincide con el inicio, el
desplazamiento es cero. Cuando Alex Crivillé da una vuelta completa al
circuito de Jerez recorre una distancia de 4.423,101 m, pero
su desplazamiento es cero. |
Rapidez
y Velocidad
Rapidez
y velocidad son dos magnitudes cinemáticas que suelen confundirse con
frecuencia.
Recuerda
que la distancia recorrida y el
desplazamiento efectuado por un móvil son dos magnitudes diferentes.
Precisamente
por eso, cuando las relacionamos con el tiempo, también obtenemos dos
magnitudes diferentes.
La rapidez
es una magnitud escalar que
relaciona la distancia recorrida con el tiempo.
La velocidad
es una magnitud vectorial que
relaciona el cambio de posición (o desplazamiento) con el tiempo.
Unidades
Tanto
la rapidez como la velocidad se calculan dividiendo una longitud entre un
tiempo, sus unidades también serán el cociente entre unidades de longitud y
unidades de tiempo. Por ejemplo:
·
m/s
·
cm/año
·
km/h
En
el Sistema Internacional, la unidad para la rapidez media es el
m/s (metro por segundo).
Rapidez media
La
rapidez media de un cuerpo es la relación entre la distancia que recorre y el
tiempo que tarda en recorrerla. Si la rapidez media de un coche es 80 km/h, esto
quiere decir que el coche coche recorre una distancia de 80 km en cada hora.
Por
ejemplo, si un coche recorre 150 km en 3 horas, su rapidez media es:
150
km / 3h = 50 km/h
Velocidad media
La
velocidad media relaciona el cambio de la posición con el tiempo empleado en
efectuar dicho cambio.
![]()
Velocidad
instantánea y rapidez instantánea
Ya
sabemos que si realizamos un viaje de 150 km y tardamos dos horas en recorrer
esa distancia podemos decir que nuestra rapidez media ha sido de 75 km/h.
Rapidez
instantánea : la rapidez en un instante cualquiera.
Rapidez
media : es la media de todas las rapideces instantáneas
y la calculamos dividiendo la distancia entre el tiempo.
Determinar
con exactitud la rapidez instantánea de un cuerpo es una tarea complicada,
aunque tenemos métodos para aproximarnos a su valor.
En
resumen, rapidez y velocidad son dos magnitudes relacionadas con el movimiento
que tienen significados y definiciones diferentes. La rapidez, magnitud escalar,
es la relación entre la distancia recorrida y el tiempo empleado. La rapidez no
tiene en cuenta la dirección. La velocidad sí
que tiene en cuenta la dirección. La velocidad es una magnitud vectorial
que relaciona el desplazamiento o cambio de la posición con el tiempo.
Rapidez constante
Si
un cuerpo se mueve y su rapidez instantánea es siempre la misma, se está
moviendo con rapidez constante. Lo mismo podemos
decir para la velocidad.
Dirección y sentido de la velocidad
Hemos
dicho que para especificar la velocidad de un móvil necesitamos: su rapidez, su
dirección y sentido. Hay muchas formas de especificar la dirección y el
sentido según que los movimientos sean de una, dos o tres dimensiones.
Dirección:
30º
Dirección:
Norte
En
el caso de los movimientos rectilíneos es mucho más sencillo. Las velocidades
en el sentido positivo son positivas y las velocidades en el sentido negativo
son negativas: el
Pero no hay ninguna razón para hacer esto, es simplemente un acuerdo.
¡El volante de un coche también es acelerador!
Es
muy importante que conozcamos cuándo está cambiando la velocidad. Como la
velocidad se compone de la rapidez y la dirección, cualquier cambio en ellas
supone un cambio en la velocidad.
Aceleración
Los
conceptos de velocidad y aceleración están relacionados, pero muchas veces se
hace una interpretación incorrecta de
esta relación.
La
aceleración relaciona los cambios de la velocidad con el tiempo en el que se
producen, es decir que mide cómo de rápidos son los
cambios de velocidad:
·
Una
aceleración grande significa que la velocidad cambia rápidamente.
·
Una
aceleración pequeña significa que la velocidad cambia lentamente.
·
Una
aceleración cero significa que la velocidad no cambia.
La
aceleración nos dice cómo cambia la velocidad y
no cómo es la velocidad. Por lo tanto un móvil puede tener una
velocidad grande y una aceleración pequeña (o cero) y viceversa.
Una característica de los cuerpos acelerados es que recorren diferentes distancias en intervalos regulares de tiempo:
|
Intervalo |
Rapidez
media |
Distancia
recorrida |
Distancia
total |
|
0
- 1 s |
5
m/s |
5
m |
5
m |
|
1
s - 2 s |
15
m/s |
15
m |
20
m |
|
2
s - 3 s |
25
m/s |
25
m |
45
m |
|
3
s - 4 s |
35
m/s |
35
m |
80
m |
Observa
que al ser diferente la rapidez media de cada intervalo, la distancia recorrida
durante el mismo es también diferente.
Aceleración constante
La
tabla anterior muestra datos de un movimiento de caída
libre, donde observamos que la rapidez cambia en 10 m/s cada segundo, es
decir que tiene una aceleración de 10 m/s/s o 10 m/s².
Aceleración media
La
aceleración (tangencial) media de un móvil se calcula utilizando la siguiente
ecuación:
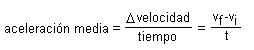
Con ella calculamos el cambio medio de rapidez en el intervalo de tiempo deseado.
Para
conocer la aceleración instantánea se puede utilizar la misma aproximación
que hicimos para el caso de la velocidad instantánea: tomar un intervalo muy
pequeño y suponer que la aceleración media en él equivale a la aceleración
instantánea.
Unidades
Como
puedes deducir de la ecuación anterior, la aceleración se expresa en unidades
de velocidad dividida entre unidades de tiempo. Por
ejemplo:
·
3
(m/s)/s
·
1
(km/h)/s
·
5
(cm/s)/min
En
el Sistema Internacional, la unidad de aceleración es 1 (m/s)/s, es decir 1 m/s².
Dirección de la aceleración
Como
la aceleración es una magnitud
vectorial, siempre tendrá asociada una dirección. La dirección del vector
aceleración depende de dos cosas:
·
de
que la rapidez esté aumentando o disminuyendo
·
de
que el cuerpo se mueva en la dirección + o - .
El
acuerdo que hemos tomado es:
Si
un móvil está disminuyendo su rapidez (está frenando), entonces su aceleración
va en el sentido contrario al movimiento.
Ecuaciones
Todos
los cálculos relacionados con las magnitudes que describen los movimientos
rectilíneos podemos hacerlos con estas dos ecuaciones:
|
x
= xo + vo·t + ½·a·t² |
|
vf
= vo + a·t |
x
es el desplazamiento del móvil
xo
es la posición inicial
t
es el intervalo de tiempo que estamos considerando
vo
es la velocidad inicial (al principio de nuestro intervalo de tiempo)
vf
es la velocidad final (al final de nuestro intervalo de tiempo).
a
es
la aceleración.
Estas
ecuaciones se pueden adaptar según las características concretas del
movimiento que estemos estudiando:
Si
el móvil parte del orígen de coordenadas
Significa
que la posición inicial xo del
cuerpo es cero. En este caso la ecuación del
desplazamiento podemos escribirla así:
|
x
= vo·t + ½·a·t² |
Si
el móvil parte del reposo
Esto
quiere decir que la velocidad inicial es cero.
Al sustituir este valor en las ecuaciones anteriores, queda:
|
x
= ½·a·t² |
|
vf
= a·t |
Si
el movimiento es uniforme
Es
el movimiento de velocidad constante, es decir el movimiento con aceleración
cero.
|
x
= vo·t |
|
vf
= vo |
No se trata de ecuaciones diferentes sino de las mismas
ecuaciones adaptadas a dos casos concretos, por tanto no es necesario que
aprendas de memoria todas las ecuaciones: con las dos
primeras y un análisis de la situación tienes suficiente.
Cómo
resolver los ejercicios
Para
resolver un ejercicio no basta con aplicar las ecuaciones. Es necesario seguir
un método o estrategia que podemos resumir así:
|
Ejemplo:
|
|
Imagina
que el conductor de una moto que circula 25 m/s pisa el freno hasta
detenerse cuando ve que el semáforo se pone en ámbar. Si los frenos
producen una aceleración de -
5 m/s², ¿cuál
será el desplazamiento durante el proceso de frenado? |
Comenzamos
haciendo un esquema informativo de la situación física, que aparece un poco más
abajo.
El
segundo paso consiste en identificar los datos que nos proporcionan. Observa que
la velocidad final vf es cero porque
nos dicen que la moto se detiene. La velocidad inicial vo
de la moto es +25 m/s porque esa es la velocidad al inicio del movimiento que
estamos estudiando (el movimiento de frenado). La aceleración a
es -
5 m/s². Presta mucha atención a los signos
+ y - que tienen las magnitudes.
|
Esquema:
|
Datos:
vo
= +25 m/s vf
= 0 m/s a
= -5 m/s² |
Buscamos: e
= ? |
El cuarto paso consiste en decidir con qué ecuación podemos calcular lo que nos piden y comprobar si tenemos todos los datos que necesitamos. En nuestro caso usaremos la ecuación:
|
x
= vo·t + ½·a·t² |
Observa
que no podemos calcular x hasta que conozcamos
el tiempo t que dura la frenada. Lo podemos
calcular con la otra ecuación:
|
vf
= vo + a·t |
Si
sustituimos los valores conocidos de vf,
vo y a,
tenemos:
0
= 25 m/s + (-5) m/s²·t
-25 m/s = -5 m/s²·t
t = -25 m/s / -5 m/s² = 5 s
Una
vez calculado el tiempo que dura el movimiento, procedemos a determinar el
desplazamiento:
x
= 25 m/s · 5s + ½ (-5)m/s²·(5s)²
x= 125 m - 62,5 m = 62,5 m
x
= 62,5 m
Hemos
llegado a la conclusión de que la moto recorre 62,5 m durante el proceso de
frenada.
El último paso consiste en comprobar que la solución que damos es correcta y razonable. La solución, en este caso, representa el desplazamiento que realiza la moto desde que se pisa el freno hasta que se detiene. Parece razonable que si se circula a 90 km/h (25 m/s), la distancia necesaria para detener la moto sea aproximadamente las dos terceras partes de un campo de fútbol, similar a la que nosotros hemos obtenido.
Para
comprobar si los cálculos matemáticos son correctos, sustituye los valores de
t y de e que hemos calculado en ambas ecuaciones del movimiento y comprueba que
la parte izquierda de cada ecuación sea igual que la derecha.
La
pendiente
El
lenguaje científico utiliza con frecuencia las gráficas porque de ellas se
pueden deducir muchas características del fenómeno que estemos estudiando. Uno
de los aspectos importantes que analizamos sobre una gráfica es su pendiente.
Así, nos interesa saber si la pendiente en un punto es positiva o negativa, si
siempre es la misma o va cambiando, etc.
La
pendiente de una gráfica en un punto es la inclinación que tiene la recta
tangente a la gráfica en ese punto.
¿Cómo se calcula la pendiente?
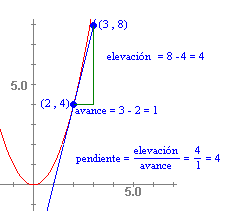
·
Selecciona
dos puntos de la recta tangente y determina sus coordenadas.
·
Calcula
la diferencia entre las coordenadas Y de los dos
puntos seleccionados (elevación).
·
Calcula
la diferencia entre las coordenadas X de dichos
puntos (avance).
·
Divide
la diferencia de coordenadas Y entre la diferencia
de coordenadas X (elevación / avance o pendiente).
En
Cinemática utilizamos con frecuencia las gráficas para extraer información
sobre las características de los movimientos que estudiamos.
De
la gráfica posición-tiempo y de la gráfica
velocidad-tiempo podemos extraer una valiosa información sobre las características
de un movimiento analizando los valores de la pendiente.
Por
ejemplo el valor de la pendiente en una gráfica posición-tiempo es la velocidad
en ese momento y en la gráfica velocidad-tiempo la pendiente equivale a la aceleración
en ese instante.
Otra
información valiosa que podemos extraer de una gráfica es el punto en que la
misma corta al eje vertical. En el caso de las gráficas x-t, este punto
representa la posicición inicial del cuerpo ya que es la posición que ocupa
cuando t=0. Si se tratara de una gráfica v-t, el punto de corte con el eje
vertical representaría la velocidad inicial, es decir la velocidad del cuerpo
cuando t=0.
Gráficas
x-t y
v-t
Una
de las formas que utilizamos para describir y estudiar los movimientos es a través
de sus gráficas posición-tiempo, velocidad-tiempo y aceleración-tiempo.
Pendiente
de las gráficas x-t
Vamos
a ver cómo podemos utilizar las gráficas posición-tiempo
para describir el movimiento. Como veremos, podemos deducir las características
de un movimiento a través del análisis de la forma y la pendiente
de las gráficas posición-tiempo (x-t). Empezaremos estudiando la relación
entre la forma de la gráfica x-t y el movimiento del cuerpo. Supongamos una
moto que se mueve hacia la derecha con una rapidez de 10 m/s. En otras palabras,
que tiene una velocidad de +10 m/s.
Si
representamos gráficamente estas parejas de valores posición-tiempo obtenemos
la siguiente gráfica:
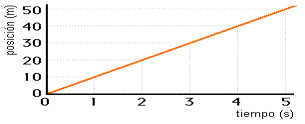 |
Observa
cómo un movimiento de velocidad positiva y constante queda representado en la
gráfica x-t por una línea de pendiente positiva (línea ascendente) y
constante (línea recta).
 |
|
Si
el movimiento es uniforme, |
Si
el movimiento es acelerado, |
|
|
|
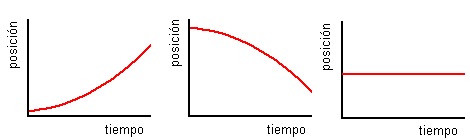
Como ves, la forma de la gráfica posición-tiempo para estos dos tipos de movimientos básicos revela una importante información:
·
Si
la velocidad es constante, la pendiente es constante (línea recta).
·
Si
la velocidad es variable, la pendiente es variable (línea curva).
·
Si
la velocidad es positiva, la pendiente es positiva (la línea es ascendente).
·
Si
la velocidad es negativa, la pendiente es negativa (la línea es descendente).
Esto
se puede aplicar a cualquier tipo de movimiento.
Las
siguientes gráficas representan objetos que se mueven con velocidad positiva y
constante.
|
Velocidad
positiva, |
Velocidad
positiva, |
|
|
|
Considera ahora las siguientes gráficas, que representan a dos cuerpos que se mueven hacia la izquierda. Para la gráfica de la izquierda deducimos que el cuerpo se mueve con velocidad negativa (porque su pendiente es negativa), constante (porque la pendiente es constante) y pequeña (porque la pendiente es pequeña). La gráfica de la derecha tiene unas características similares aunque se trata de un movimiento más rapido porque su pendiente es mayor que la de la izquierda. Una vez que hayas practicado un poco te resultará más fácil.
|
Lento,
Hacia la izquierda (-) |
Rápido,
Hacia la izquierda (-) |
|
|
|
Ejercicios
Supongamos una moto que se mueve con velocidad constante de +10 m/s. Como ya sabes, si un cuerpo se mueve con velocidad constante su aceleración es cero.
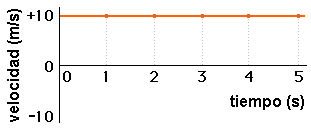
Se obtiene una recta horizontal, cuya pendiente es cero en todos los puntos.

Se trata de una recta ascendente, es decir de pendiente constante y
positiva.
Como
ya hemos dicho, la pendiente de una gráfica v-t es la aceleración por lo que
el movimiento de la moto es de aceleración constante y positiva.
Los
movimientos de aceleración constante son uniformemente
acelerados.
|
Movimiento
Uniforme |
M.
Uniformemente Acelerado |
|
|
|
La
forma de la gráfica velocidad-tiempo para estos dos tipos de movimientos revela
una importante información:
·
Si
la aceleración es constante, la pendiente es constante (línea recta).
·
Si
la aceleración es cero, la pendiente es cero (línea recta horizontal).
·
Si
la aceleración es positiva, la pendiente es positiva (la línea es ascendente).
·
Si
la aceleración es negativa, la pendiente es negativa (la línea es
descendente).
Esto
se puede aplicar a cualquier tipo de movimiento.
Veamos algunos casos:
|
Movimiento
Uniforme |
|
|
|
Velocidad
positiva porque se mueve hacia la derecha |
|
Movimiento Uniforme |
|
|
|
Velocidad
negativa porque se mueve hacia la izquierda |
|
Movimiento uniformemente acelerado |
|
|
|
Velocidad
positiva porque se mueve hacia la derecha |
|
Movimiento uniformemente acelerado |
|
|
|
Velocidad
positiva porque se mueve hacia la derecha |
|
Movimiento uniformemente acelerado |
|
|
|
Velocidad
negativa porque se mueve hacia la izquierda |
|
Movimiento uniformemente acelerado |
|
|
|
Velocidad
negativa porque se mueve hacia la izquierda |
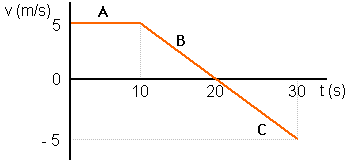
Ejercicios
Utilizando
tus conocimientos sobre la pendiente y su significado en las gráficas
velocidad-tiempo, describe los movimientos representados a continuación.
Indica, para cada tramo, si se trata de velocidad positiva o negativa, si el
movimiento es uniforme o acelerado y si los posible cambios de velocidad son de
lento a rápido o de rápido a lento, es decir si la aceleración es positiva o
negativa. Intenta ser completo en tu descripción, realizando todos los cálculos
que puedas.
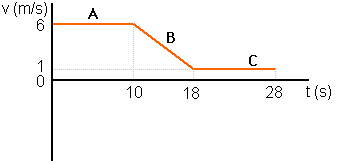
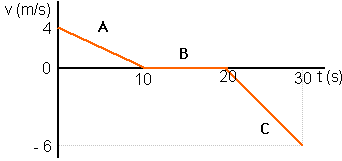
Área
de la gráfica v-t
Ya
hemos visto cómo se puede determinar la
aceleración de un móvil mediante la gráfica
v-t,
pero no es lo único que podemos analizar en una gráfica velocidad-tiempo.
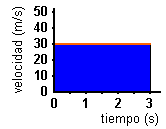
La
gráfica corresponde a un móvil
que se desplaza con una velocidad constante de 30 m/s. El área azul representa
la distancia recorrida por el móvil entre t = 0 y t = 3 s. Se trata de un rectángulo
cuya base es 3 s y cuya altura es 30 m/s.
Área
= 3 s · 30 m/s = 90 m
Por
tanto durante los tres segundos que dura el movimiento, el móvil recorre una
distancia de 90 m.
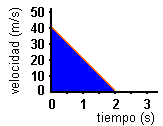
En
la gráfica se representa el movimiento de aceleración negativa de un móvil
que parte con velocidad inicial de 40 m/s y que se detiene a los 2 s.
Área
= 0,5 · 2s · 40m/s = 40 m
La
distancia recorrida en dos segundos es 40 m.
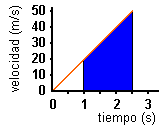
El
área marcada en este caso representa la distancia recorrida por el móvil entre
1s y 2,5s.
Área
= 0,5 · 1,5 s ·(20 m/s + 50 m/s) = 52,5 m
En
este caso, por tanto, el móvil recorre 52,5 m.
Un
método alternativo para calcular el área del trapecio consiste en
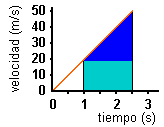
Área del rectángulo = b · h = 1,5 s · 20 m/s = 30 m
Como puedes observar la suma de estas dos áreas es 52,5 m, como habíamos
calculado antes.
Vamos
a estudiar ahora un caso un poco más complicado.
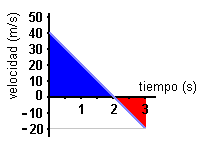
El movimiento representado en la gráfica de la izquierda tiene velocidad positiva en el intervalo comprendido entre 0 y 2s y velocidad negativa en el segundo siguiente. Ya hemos calculado más arriba que el área del triángulo azul equivale a un desplazamiento de 40 m. Por su parte, el triángulo rojo representa un desplazamiento de:
Área
= ½ · b · h = 0,5 · 1
s ·(-
20)
m/s = -10 m
El
signo negativo nos indica que la distancia ha sido recorrida en sentido
contrario. Por lo tanto en este caso la
distancia recorrida y el desplazamiento son diferentes:
distancia
recorrida = 40 m
(derecha) y 10 m (izquierda) = 50 m
desplazamiento = 40 m - 10 m =
30 m
Como habrás observado para calcular la distancia recorrida sumamos las áreas sin considerar su signo, mientras que para determinar el desplazamiento sí se consideran los correspondientes signos.