PHYSICS 100A SELF TEST (1)

1.A hunter aims directly at a target (on the same level) 120m away. (a) If the bullet leaves the gun at a speed of 250m/s, by how much will it miss the target? (b) At what angle should the gun be aimed so the target will be hit?

Solution. (a) We choose a coordinates system with the origin at the release point, with x horizontal and y vertical with the positive direction down. We find the time of flight from the horizontal motion.

                  x = x₀ + v₀t;

                 120m = 0 + (250m/s)t, which gives t = 0.480s.

            We find the distance the bullet falls from

                  y = y₀+ v_0yt + 1/2at²;

                  y = 0 + 0 + 1/2(9.80m/s²)(0.480s)² = 1.13m.

        (b) The bullet will hit the target at the same elevation, so we can use the expression for the horizontal range:

                 R = v₀²sin(2q₀)/g;

                120m = (250m/s)sin(2q₀)/(9.80m/s²), which gives sin(2q₀) = 0.0188, or 2q₀ = 1.08°, or q₀ = 0.54°.

             The larger angle of 89.5° is not realistic.

2. A 2.5 N force is uniformly applied to a 1.5kg- cart at rest. (a) After 10 seconds how far away the car is traveling?  (b) At that time the 2.5-N force is removed. What force is needed to stop the cart in 10m?

Solution. (a) We find the acceleration of the cart from

                         F = ma

                         25N = (1.5kg)a, which gives a = 1.67m/s².

                  We find the distance the car travels in 10s from

                          x = x₀ + v₀t + 1/2at²;

                          x = 0 + 0 + 1/2(1.67m/s²)(10s)² = 83.33m.

             (b) We find the velocity of the car at t = 10s from

                          v = v₀ + at = 0 + (1.67m/s)(10s) = 16.7m/s.

                   We find the acceleration of the cart when the cart is decelerating from

                          v² = v₀² + 2a(x - x₀)

                          0 = (16.7m/s)² + 2a(10m - 0);  which gives a = -13.94m/s^2.

                   We find the force from

                          F = ma = (1.5kg)(-13.94m/s²)  = -20.92N.

                   The force is in the opposite direction.

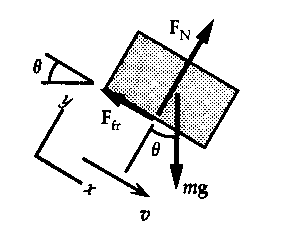
3. An 18.0-kg box is released on a 37.0 incline and accelerates down the incline at 0.270m/s. Find the friction force impeding its motion. How large is the coefficient of friction?

Solution While the box is sliding down, friction will be up the place, opposing the motion. From the force diagram for the box, we have SF = ma:                    x-component:    mgsin q - Ffr = ma;                   y-component:    F - mgcos q = 0.             From the x-equation, we have                  Ffr = mgsin q - ma = m(gsin q - a)                       = (18.0kg)[(9.80m/s2)sin37.0° - (0.270m/s2)]                       = 101N.            Because the friction is kinetic, we have                    Ffr = mkFN = mkmgcos q;                   101.3N = mk = 0.719.

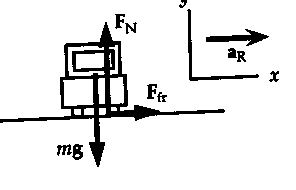
  4. A car is to make a turn around a level curve of radius 80m at a speed of 60km/h. What is the minimum value of coefficient of friction between the tires and the road that the car will not skid?       

Solution. The friction force provides the centripetal acceleration. We take a coordinate system with the x-axis in the direction f the centripetal acceleration.              We write SF = ma from the force diagram for the car:                       x-component:  Ffr = ma = mv2/r;                       y-component:  FN - mg = 0.              If the car does not skid, the friction is static, with Ffr < msF.              Thus we have                       mv2/r < msmg, or                      ms > v2/gr = [(60km/h)(1000m/km)/(3600s/h)]2/(9.80m/s2)(80m) = 0.35.              Thus ms > 0.35.