100A Self Test 2

1. A 4.00-kg block is given an initial speed of 8.00m/s at the bottom of a 20.0° incline. The frictional force that retards its motion is 15.0N. (a) If the block is directed up the incline, how far does it move before stopping? (b) Will it slide back down the incline?

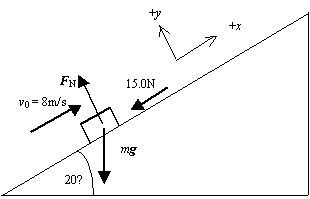
   Solution. (a) We draw free-body diagram and choose the coordinate system as shown. We take y = 0 at the bottom of the incline.               The non-conservative force is friction force. The normal is perpendicular to the direction of motion hence it does not do work.               Thus we have                              WNC = Ffrd                The energy of the block at the bottom of the incline is                              Ei = KEi + PEi = 1/2mv02 + 0;               The energy of the block when the block stops is                              Ef = KEf + PEf = 0 + mgy;               We find y from                                y = dsin20°.               From conservation of energy we have                            - WNC = DE = Ef  -  Ei = mgy - 1/2mv02;                           -(15.0N)d = (4.00kg)(9.80m/s)dsin20° - 1/2(4.00kg)(8.00m/s)2,                 which gives d =4.51m             (b) On the incline the forces acting on the block along the surface are mgsin20.0° and  Ffr;                    since                            mgsin20.0° = 13.4N < 15N = Ffr,                   the block will not slide back down the incline.

2. A softball of mass 0.220kg that is moving with a speed of 5.5m/s collides head-on and elastically with another ball initially at rest. afterward it is found that the incoming ball has bounced back with a speed of 3.7m/s. Calculate (a) the velocity of the target ball after the collision, and (b) the mass of the target ball.

   Solution.

   (a) For the elastic collision of the two balls., we use momentum conservation:

                   m₁v₁ +  m₂v₂  =  m₁v₁' + m₂v₂';

                  (0.22kg)((5.5m/s) + m₂(0)  = (0.22kg)(-37m/s) + m₂v₁'.

        Because the collision is elastic, the relative speed does not change:

                  v₁ - v₂ = -(v₁' - v₂'), or 5.5m/s - 0 = v₁' - (-3.7m/s), which gives   v₂' = 1.8m/s.

    (b) Using the result for v₂' in the momentum equation, we get   m₂ = 1.1kg.

3.  A 5-m, 15-kg uniform ladder leans against a smooth wall as shown. Find the coefficient of static friction between the ladder and the ground that the ladder does not slide.

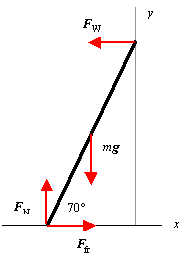
   Solution.  We choose the coordinate system as shown.                We write SF = ma from the force diagram:                x- component: SFx = Ffr - FW = 0;                y- component: SFy = FN - mg = 0.               From  FN = mg  and Ffr  = msFN, we have                            FW = Ffr  = msmg.              We write St = 0 about the pivot at ground:                            St  = mg(1/2)(5m)cos70° - FW(5m)sin70° = 0, which gives                           FW = 1/2mgcos70°/sin70° = (1/2)(15kg)(9.80m/s2)cos70°/sin70° = 26.75N = Ffr .             Thus we have                             ms = Ffr/FN = (26.75N)/[(15kg)(9.80m/s2)] = 0.182

4. A ping-Pong ball has a diameter of 3.8cm and average density of 0.084g/cm. What force would be required to hold it completely submerged under water?

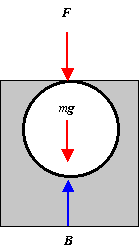
   Solution. At equilibrium,  SF = 0 or                            F + mg - B = 0, where B is the buoyant force.               Thus we have the applied force from                            F = B - mg               We calculate B from B = rwaterVg, and we find the mass of the ball from                           m = V rballg, so we have                           F = Vg(rwater -  rball) = 4/3pr3g(rwater -  rball)                              = 4/3p(1.90 x 10-2m)3(9.80m/s2)(103kg/m3 - 84kg/m3)                              = 0.258N.