100A SELF TEST 3

1. A brass plug is to be placed in a ring made of iron. At room temperature, the diameter of the plug is 8.753cm and that of the inside of the ring is 8.743cm. They must both be brought to what common temperature in order to fit?

   Solution.

   We can treat the change in diameter as a simple change in length, so we have

                  D = D₀(1 + aDT).

   The two objects must reach the same diameter:

                 D = D_0brass(1+ a_brassDT) = D_0iron(1+ a_ironDT);

                (8.753cm){1 + [19 x 10^-6(C°)^-1](T- 20°C)} = (8.743cm){1 + [12 x 10^-6(C°)^-1](T- 20°C)};

            which gives

                 T = - 1.4 x 10²C°.

2. (a) What is the pressure inside a 50.0-L container holding 105.0kg of argon gas at 20°C? (b) If the same amount of argon expands its volume to 80.0L what is its pressure at 20°C?

   Solution.

   (a) If we assume argon is an ideal gas, we have

                 PV = nRT = (m/M)RT;

                P(50.0 x 10^-3m³) = [(105.0kg)(10³g/kg)/(40g/mol)](8.314J/mol.K)(293K),

       which gives P = 1.28 x 10⁸Pa = 1.26 x 10³atm.

   (b) Because the temperature is constant, we have

               P₁V₁ = P₂V₂;

               (1.26 x 10³atm)(50.0L) = (80.0L)P₂. which gives P₂ = 7.86 x 10²atm.

3. The specific heat of mercury is 138j/kg.C°. determine the latent heat of fusion of mercury using the following calorimeter data: 1.00kg of solid Hg at its melting point of -39.0°C is placed in a 0.620-kg aluminum calorimeter with 0.400kg of water at 12.80°C; the resulting equilibrium temperature is 5.06°C.

   Solution. 

   We find the latent heat of fusion from

                heat lost = heat gained;

               (m_Alc_Al + m_waterc_water )DT = m_Hg(L_Hg + c_HgDT_Hg )

               [(0.620kg)(900J/kg.°C) + (0.400kg)(4186J/kg.°C)](12.80°C -5.06°C) =

                       (1.00kg){L_Hg + (138J/kg.°C)[5.06°C - (-39.0°C)]},

   which gives L_Hg = 1.12 x 10J/kg.                  

4. When a gas is taken from a to c along the curved path in Figure, the work done by the gas is W = -35J and the heat added to the gas is Q = -63J. Along path abc, the work done is W = -48J. (a) What is Q for path abc? (b) If P_c = 1/2P_b, what is W for path cda? (c) What is Q for path cda? (d) What is U_a - U_c? (e) If U_d - U_c = 5J, what is Q for path da?

   Solution.

   (a) We can find the internal energy change  Uc - Ua from the information for the curved path a® c:                    Uc - Ua = Qa®c - Wa®c = -63J - (-35J) = -28J.       For the path a®b®c,, we have                   Uc - Ua = Qa®b®c - Wa®b®c = Qa®b®c - Wa®b;                   -28J = Qa®b®c - (-48J), which give Qa®b®c = -76J. (b) For the path c®d®a, work is done only during the constant pressure process, c®d, so we have                  Wc®d®a = Pc(Vd -Vc) = 1/2Pb(Va -Vb)                                  = 1/2Wb®a = -1/2Wa®b  = -1/2(-48J) = +24J. (c) We use the first law of thermodynamics for the path c®d®a to find Qc®d®a:                 Ua - Uc = -( Uc - Ua) = Qc®d®a - Wc®d®a;                 -(-28J) = Qc®d®a - (-24J),  which gives  Qc®d®a = +52J. (d) Ua - Uc = -(Uc - Ua) = -(-28J) = +28J. (e) Because there is no work done for the path d®a, we have                 Ua - Ud = (Ua - Uc) + (Uc - Ud) = (Ua - Uc) - (Ud - Uc)                  = Qd®a - Wd®a;                 +28J - (+5J) = Qd®a - 0, which gives Qd®a = +23J.
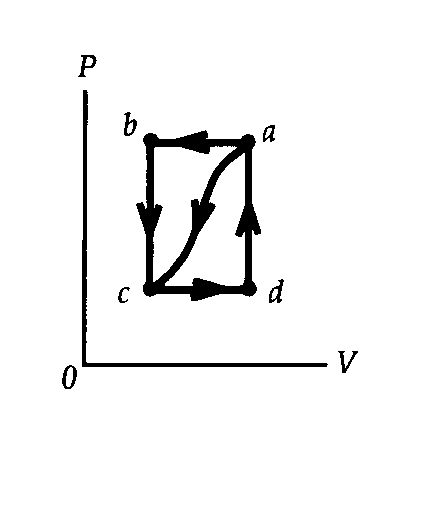