100B Self Test 2

1. (a) Determine the magnetic field midway between two long straight wires 2.0cm apart when they carry currents of 10A and 15A respectively in the same direction. (b) A 10-m wire carrying 3-A current in the opposite direction is placed parallel midway between the two wires. Find the force exerted on the third wire.

   Solution,

   (a) When the currents are in the same direction, the fields between the currents will be in opposite directions, so at the midpoint we have                     Ba = B2  - B1  = [(m0/4p)2I2/r] -  [(m0/4p)2I1/r] = [(m0/4p)2/r](I2 - I1)                          = (10-7T.m/A)2/(0.010m)(15A - 10A)                          = (1.0 x 10-4T up, with the currents as shown.
   (b) We find the force exerted on the third wire from                     F = IBL = (3A)(1.0 x 10-4T)(10m) = 3 x 10-3N.        Using right-hand rule the force is to the left.        Thus the force exerted on the third wire is 3 x 10-3N to the left.

2. A 40-cm conducting rod is moved to the right on a U-shaped conductor in a uniform magnetic field B of 0.15T as shown. The rod's resistance is 0.5, At a certain instant the resistance of the U-shaped conductor is 2.0W, and the power dissipated in the combination is 0.0625W. What is the rod's speed at this instant?

   Solution. We find the induced emf at the instant from                       e = Blv = (0.15T)(0.4m)v. (1)                 Because the rod and the U-shaped conductor are connected in series we find the resistance of the combination from                        R = 0.5W + 2.0W = 2.5W.                  Because the power dissipated in the combination is 0.625W, we have                       P =  e2/R;          (3)                 Combining the equations (1) and (3) we have                     ( blv)2 = PR;                    [(0.15T)(0.4m)]2v2 = (0.0625W)(2.5W),  which gives v = 6.59m/s

3. A drinking glass is 4.00cm wide at the bottom, as shown in figure. When an observer's eye is placed as shown, the observer sees the edge of the bottom of the glass. When this glass is filled with water, the observer sees the center of the bottom of the glass. Find the height of the glass.

   Solution. From the diagram we have                         tan q1 = 4/h    and      tanq2 = 2/h                        tan2 q1 = 4tan2 q2            (1)                        sin2 q1/(1 -  sin2 q1) =  4sin2 q2/(1 -  sin2 q2)                        n1sinq1 =  n2sinq2               or        sinq1 = 1.333sinq2                    Squaring both sides,                         sin2 q1 = 1.778sinq2                 Substituting this value into (1), which gives                        1.778sin2 q2/(1 - sin2 q2) = 4sin2 q2/(1 -  sin2 q2)                Defining x = sin2 q2 and solving for x,                        0.444/(1-1.778x) = 1((1 - x)                        0.444 - 0.444x = 1 - 1.778x               and    x = 0.417 = sin2 q2                    Thus                        q2  = sin-1(0.417)1/2 = 40.2°              and                        h = (2.00cm)/tanq2 = (2.00cm)/tan42.0° = 2.37cm.

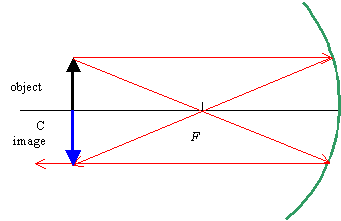
4. Where should an object be placed in front of a concave mirror so that it produces an image at the same location? (b) Is the image real or virtual? (c) Is the image inverted or erect? (d) What is the magnification of the image?

   Solution.    (a) With di = do , we located the object from                        (1/di) + (1/do) = 1/f ;                         (1/do) + (1/do) = 1/f,  which gives  do = 2f = r.        The object should be placed at the center of curvature.  (b) Because the image is in front of the mirror, di > 0, it is real.  (c) The magnification is                         m = -di/do = do/do = -1.       Because the magnification is negative, the image is inverted.  (d)  As found in part (c), m = -1.