CHAPTER 13

1. (P.409 Prob.52) Calculate by direct integration the moment of inertia for a thin rod of mass M and length L about an axis located distance d from one end. Confirm that your answer agrees with Table 13.3 when d = 0 and when d = L/2.
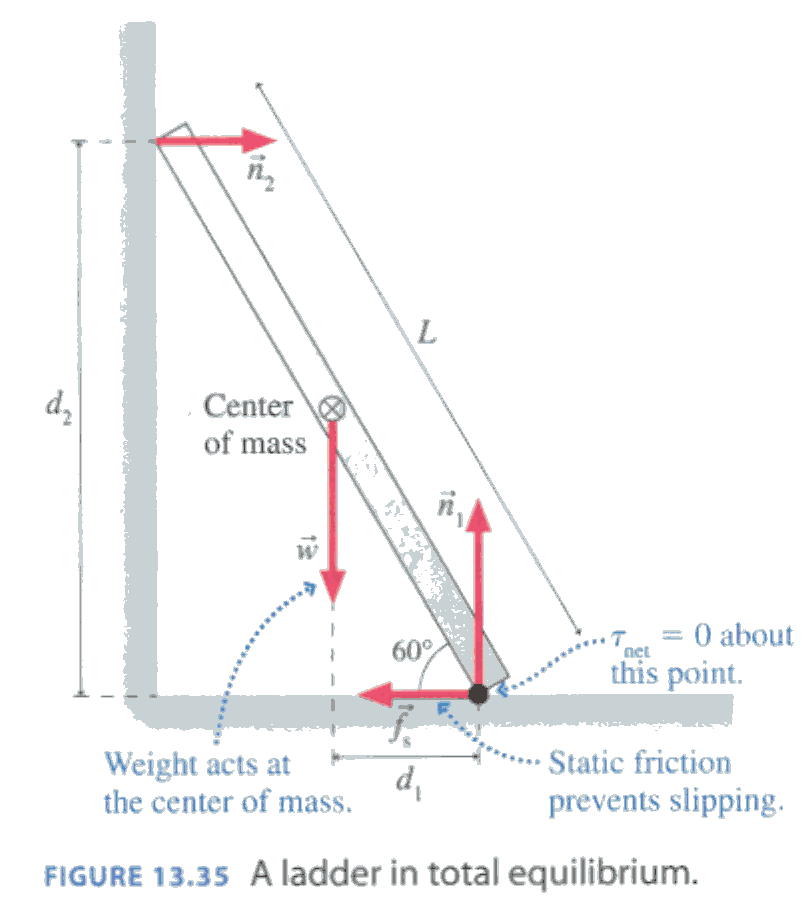
2. (P.410 Prob.60) A 3.0-m-long ladder, as shown in Figure 13.35, leans against a frictionless wall. The coefficient of static friction between the ladder and the floor is 0.40. What is the minimum angle the ladder can make with the floor without slipping?
   
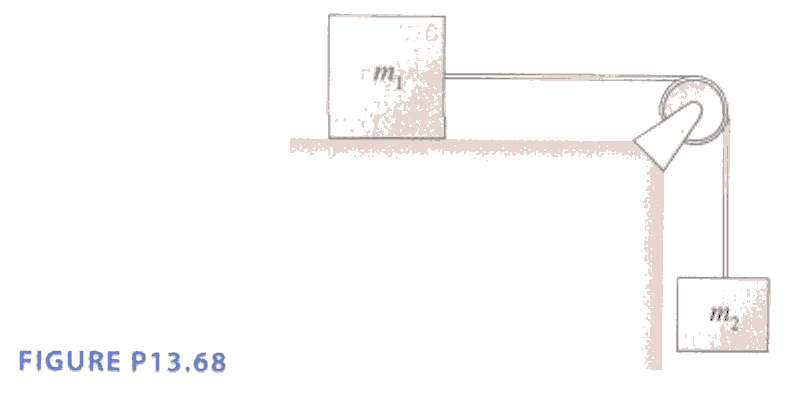
3. (P.410 Prob.68) Blocks of mass m₁ and m₂ are connected by a massless string that passed over the frictionless pulley in Figure P13.68. Mass m₁ slides on a horizontal, frictionless surface. Mass m₂ is released while the block are at rest.
   a. Assume the pulley is massless. Find the acceleration of m₁ and tension in the string This is a Chapter 8 review problem.  
   b. Suppose the pulley has mass m_p and radius R. Find the acceleration of m₁ and the tension in the upper and lower portions of the string. Verify that your answers agree with part a if you set m_p = 0.
   
4. (P.411 Prob.74) A long, thin rod of mass M and length L is standing straight up on a table. Its lower end rotates on a frictionless pivot. A very slight push causes the rod to fall over. As it hits the table, what are (a) the angular velocity and (b) the speed of the tip of the rod?
5. (P.411 Prob.80) A merry-go-round is a common piece of playground equipment. A 3.0-m-diameter merry-go-round with a mass of 250 kg is spinning at 20 rpm. John runs tangent to the merry-go-round at 5.0 m/s, in the same direction that it is turning and jumps onto the outer edge. John's mass is 30kg. What is the merry-go-round's angular velocity, in rpm after John jumps on?
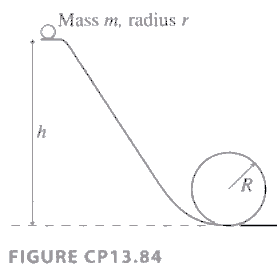
6. (P.412 Prob.84) Challenge Problem. The marble rolls down a track and around a loop-the -loop of radius R. The marble has mass m and radius r. What minimum height h must the track have for the marble to make it around the loop- the-loop without falling off?