CHAPTER 10

  1. From conservation of energy
    Kf + Uf = Ki + Ui
    1/2mvf2 + mgyf = 1/2mvi2 + mgyi;
    1/2vf2 + 0 = 1/2(80 m/s)2 + (9.8 m/s2)(10 m), vf = 81.2 m/s.
  2. In Figure P10.38a, use conservation of energy
    Kf + Uf = Ki + Ui;
    1/2mvf2 + 1/2kxf2 = 1/2mvi2 + 1/2kxi2;
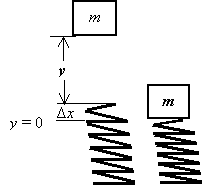
    mv02 + 0 = 0 + k(Dx)2, k = m(v0/Dx)2.
    In Figure P10.38b, use conservation of energy
    Kf + Uf = Ki + Ui;
    1/2mvf2 + 2 x 1/2kxf2 = 1/2mvi2 + 2 x 1/2kxi2
    mvf2 + 0 = 0 + 2k(Dx)2,
    mvf2 + 0 = 0 + 2[m(v0/Dx)2](Dx)2, vf = (Ö2)v0.
  3. Conservation of energy
    Kf + Uf = Ki + Ui
    0 + mgyf + 1/2kxf2 = 0 + mgyf + 1/2kxf2;
    (1000 kg)(9.8 m/s2)(2.0 m + 0.5 m) + 0 = 0 + 1/2k(0.5 m)2,  k = 1.96 x 105 N/m.

  4. In order for the ball to go over the top of the peg without the string going slack, the ball must follow a circular path. At the lowest point
    Fnet = mg = mv2/r, v2 > gr = g(L/3).
    From conservation of energy for the ball
    Ui = Kf,
    mg(L - Lcosθ) = 1/2mv2;
    gL(1 - cosθ) = 1/2v2 > 1/2gL/3
    cosθ < (1 - 1/6) = 5/6, θ > cos-1(5/6) = 33.6°
  5. a. Use Galilean transformation of velocities, where V = -3.0 m/s. 
        (vix)1' = (vix)1 - V = 4.0 m/s - (-3.0 m/s) = 7.0 m/s.
        (vix)2' = (vix)2 - V = -3.0 m/s - (-3.0 m/s) = 0 m/s.
        In 200-g ball's frame we have
        (vfx)1'  = [(m1 -  m2)/(m1 + m2)](vix)1' = [(0.1 kg - 0.2 kg)/(0.1 kg + 0.2 kg)](7.0 m/s) = -2.33 m/s                                          
        (vfx)2'  = [(2m1)/(m1 + m2)](vix)1' = [2(0.1 kg)/(0.1 kg + 0.2 kg)](7.0 m/s) = 4.67 m/s    
     In lab frame we have
         (vfx)1 = (vfx)1'  + V = (-2.33 m/s) + (-3.0 m/s) = -5.33 m/s                                       
         (vfx)2 = (vfx)2'  + V = (4.67 m/s) + (-3.0 m/s) = 1.67 m/s
    So, 100-g ball moves to the left at 5.33 m/s, and 200-g ball moves to the right at 1.67 m/s.
    b. If the collision is perfectly inelastic.
        m1(vix)1 + m2(vix)2 = (m1 + m2)vf
       (0.1 kg)(4.0 m/s) + (0.2 kg)(-3.0 m/s) = (0.1 kg + 0.2 kg)vf,
       vf = - 0.67 m/s
    Both balls move to the left with a speed of 0.67 m/s
  6. a. When the spring is compressed at maximum the collision is perfectly inelastic.
    7. Conservation of momentum:
      m1(vix)1 + m2(vix)2 = (m1 + m2)(vfx)
      (2.0 kg)(4.0 m/s) + 0  = (2.0 kg + 1.0 kg)(vfx)
      vfx  = 2.67 m/s
    Conservation of energy:
    1/2m1(vix)12 = 1/2(m1+ m2)(vfx)2 + 1/2k(Dx)2
    (2.0 kg)(4.0 m/s) + 0  = (2.0 kg + 1.0 kg)(2.67 m/s)2 + (5000 N/m)(Dx)2
     Dx = 2.1 x 10-3 m = 2.1 mm.
    b. When the spring relaxes the 2.0-kg cart still moves with the same speed of 2.67 m/s.
        The elastic potential energy of the spring converts to part of the kinetic energy of the 1.0-kg cart
         1/2k(Dx)2 + 1/2m2(vfx)2 = 1/2(m2)(vfx)22
         1/2(5000 N/m)(2.1 x 10-3 m)2 + 1/2(1.0 kg)(2.67 m/s)2 = 1/2(1.0 kg)(vfx)22
         (vfx)2 = 2.674 m/s.