CHAPTER 11

1. Path ABD:
   W = ò₀^3m(6i + 8j) N·idx + ò₀^4m(6i + 8j) N·jdy
       = (6 N)(x)|₀^3m + (8 N)(y)|₀^4m
       = 50 J.
   Path ACD:
   W = ò₀^4m(6i + 8j) N·jdy + ò₀^3m(6i + 8j) N·idx
       = (8 N)(y)|₀^4m +  (6 N)(6 N)(x)|₀^3m
       = 50 J.
   Path AD: dW = F·dr = [(6² + 8²)^1/2 N]dr N= (10 N)dr
   W = ò₀^5m(10 N)dr m = 50 J.   
   As W_ABD= W_ACD = W_AD, i.e., the work done is independent of the paths, the force is conservative.
2. (a) The work  done by the external force is 
        W_ext = FLcosθ
       DE = (K_f  - K_i ) + (U_f - U_i ) = (1/2mv_f² - 0) + (0 - mglsinθ) 
       W_ext = DE 
         v_f = Ö2[-(200 N)(50 m)cos20° + (75 kg)(9.8 m/s²)(50 m)sin20°]/(75 kg) = 9.21 m/s.
   (b) Use Newton's laws, the force
   
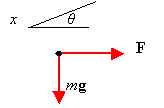
        From free-body diagram
        SF_x = mgsinθ - Fcosθ, a_x = SF_x/m = (mgsinθ - F)/m = [(75 kg)(9.8 m/s²)sin20° - (200 N)cos20°)]/(75 kg) = 0.85 m/s².
        v_f² = v₀² + 2a_xL;
        v_f = Ö0 + 2(0.85 m/s²)(50 m) = 9.22 m/s.
   The two results are same.
3. (a) By conservation of energy DE = 0.
         K_f  + U_f  =  K_i  + U_i;
        1/2(m₁ + m₂)v_f² + 0 =  0 + m₂gy;
         v_f = Ö2m₂gy/(m₁ + m₂)
             = Ö2(2.0 kg)(9.8 m/s²)(1.5 m)/(1.0 kg + 2.0 kg) 
             = 4.43 m/s.
   (b) W_ext = DE
         - fL = K_f  - K_i  + U_f  - U_i = 1/2(m₁ + m₂)v_f² - 0 + 0 - m₂gy
         -μ_km₁gL = 1/2(m₁ + m₂)v_f² - m₂gy;
          v_f = Ö2[(2.0 kg)(9.8 m/s²)(1.5 m) - (0.15)(1.0 kg)(9.8 m/s²)(1.5 m)]/(1.0 kg + 2.0 kg)
              = 4.26 m/s.
4. The force the gardener exerts on the lawnmower is F. In order to push the lawnmower at constant speed Fcosθ = f (frictionn)
   
   
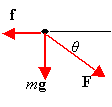
      f = μ_k(mg + Fsinθ) = Fcosθ,
     F = μ_kmg/(cosθ - μ_ksinθ) = (0.15)(12 kg)(9.8 m/s²)/(cos37° - 0.15sin37°) = 24.9 N.
   The power supplied by the gardener is
     P = Fv = (24.9 N)(1.2 m/s) = 29.9 W = 0.04 hp.
5. Find the speed at the top of the incline using conservation of energy.
   1/2mv_f² = 1/2kx² - mgy - μ_kmgsinθy/sinθ
               v_f² = 2[1/2(1000 N/m)(0.15 m)² - (0.2 kg)(9.8 m/s²)(2.0 m) - (0.2)(0.2 kg)(9.8 m/s²)(2.0 m)]/(0.2 kg)
                    = 65.46 (m/s)²
   Find d from the equation of range of projectile 
               d = v_f²sin2θ/g
                  = (65.46 m²/s²)sin(2 x 45°)/(9.8 m/s²)
                  = 6.68 m.