CHAPTER 13

1. Take the axis as origin and the x-coordinates of the two ends are x = -d and x = L - d, respectively
   Find the moment of inertia.
   I = ò_-d^L-d(M/L)x²dx = (1/3)(M/L)x³|_-d^L-d
     = (1/3)(M/L)[(L - d)³ - (-d)³]
     = (1/3)(M/L)(L³ - 3L²d + 3Ld² - d ³+ d³)
     = M[(1/3)L² - d(L - d)]
   When d = 0, I = (1/3)ML²
   When d = L/2, I = M[(1/3)(L)² - (L/2)(L - L/2)] = (1/12)ML²
   Both results agree with Table 13.3
2. Take the point where the ground supports the ladder as the pivot point.
   SF_x = n₂ - f_s = 0
   SF_y = n₁ - mg = 0
   τ_net = (L/2)cosθmg - Lsinθn₂ = 0
   n₂ = (1/2)mg/tanθ = f_s = μ_sn₁ = μ_smg
    f_s < μ_smg
   (1/2)mg/tanθ < μ_smg
   tanθ > (1/2)μ_s
    θ _min= tan^-1(1/2)/μ_s = tan^-1[(1/2)/(0.40)] = 38.7°
3. a. From the free-body diagram
   
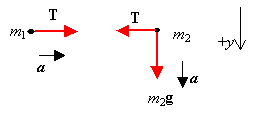
   T = m₁a,  m₂g -T = m₂a.
   Combine two equations to find the acceleration a = m₂g/(m₁ + m₂), and the tension T = m₁m₂g/(m₁ + m₂)
   b. From the free-body diagram
   
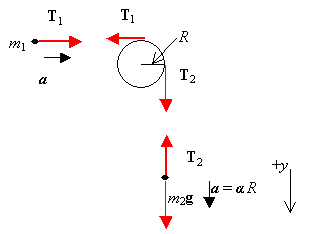
   For m₁,  T₁ = m₁a.
   For the pulley, (T₂ - T₁)R = Iα = (1/2)m_pR²(a/R) = (1/2)m_paR,, or T₂ - T₁ = (1/2)m_pa.
   For  m₂, m₂g -T₂ = m₂a.
   Combine three equations to eliminate T₁ and T₂ and to find a.
   a = m₂g/(m₁ + m₂ + m_p/2)
   Then T₁ = m₁a = m₁m₂g/(m₁ + m₂ + m_p/2), T₂ = m₂g - m₂a = m₂g(m₁ + m_p/2 )/(m₁ + m₂ + m_p/2)
   When m_p = 0, a = m₂g/(m₁ + m₂), and T₁ = T₂ = m₁m₂g/(m₁ + m₂)
   This agrees with part a.
4. (a) From conservation of energy we have
   
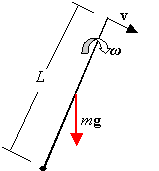
   DE = E_f - E_i = K_rot - U_i = 1/2Iω² - Mg(1/2)L = 0.
     (1/2)(1/3)(ML²)ω² - (1/2)MgL = 0,  ω² = (3g/L)^1/2.
   (b) v = ωr = (3g/L)^1/2 L = (3gL)^1/2
5. Use conservation of angular momentum.
   L_f = L_i.
   I_{merry-go-round+John}ω_f = I_{merry-go-round}ω_i+ m_Johnv_Jonh,iR
   [1/2(m_{merry-go-round}R²) + m_JohnR²]ω_f = (1/2)(m_{merry-go-round}R²)ω_i + m_Johnv_Jonh,iR
   [(1/2)(250 kg) + (30 kg)](3.0 m/2)²]ω_f = (1/2)(250 kg)(3.0 m/2)²[(20 rpm)(2π rad/rev)/(60s/min)] + (30 kg)(5.0 m/s)(3.0 m/2),
   ω_f = 2.33 rad/s.
6. To make the marble on the loop without falling off we have
    mv²/R > mg, then v² > gR.
   Use conservation of energy.
    DE = U_f + K_tran,f + K_rot,f - U_i + K_tran,i + K_rot,i = 0.
     mg(2R) + 1/2mv² + 1/2Iω² - mgh = 0;
     mg(2R) + 1/2mgR + (2/5)(mr²)(v/R)² - mgh = 0,
     mg(2R) + 1/2mgR + (2/5)(mr²)(g/R) -mgh = 0;
    h_min = (3/2)R + (2/5)(r²/R)