CHAPTER 3

  1. (a)

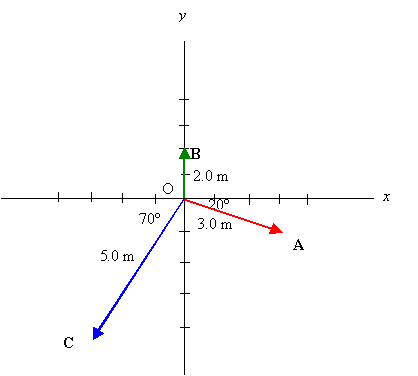
    (b) A = (3.0 m)cos20°i - (3.0m)sin20°j = (2.82 m)i - (1.01m)j
         B =  0i + (2.0 m)j = (2.0 m)j
         C = -(5.0 m)cos70°i + (-5.0 m) sin70°j = -(1.71 m)i - (4.70 m)j
    (c) Dx = Ax + Bx + Cx=  2.82 m + 0 m  -1.71 m = 1.11 m.
         Dy = Ay + By + Cy= -1.01 m + 2.0m  - 4.70 m = -3.71 m
         D = (Dx2 + Dy2)1/2 = [(1.11 m)2 + (-3.71 m)2]1/2 = 3.87 m
         q = tan-1(Dy/Dx) = tan-1(-3.71 m/1.11 m) = 73.3° (south of west)
  2. a. At t = 0 s, r = (5i + 4j)(0) m = 0 m, so the distance from the origin is 0 m.
        At t = 2 s,  r = (5i + 4j)(2 s)2 m = (20i + 16j) m, |r| = [(20)2 + (16)2]1/2 m = 25.6 m.
        At t = 5 s,  r = (5i + 4j)(5 s)2 m = (125i + 100j) m, |r| = [(125)2 + (100)2]1/2 m = 160.1 m.
    b. We find the velocity from v = dr/dt = d[(5i + 4j)t2]/dt = (10i + 8j)t m/s.
    c. At t = 0 s, v = (10i + 8j)(0 s) m/s = 0 m/s.
        At t = 2 s, v = (10i + 8j)(2 s) m/s = (20i + 16j) m/s.
        At t = 5 s, v = (10i + 8j)(5 s) m/s = (50i + 40j) m/s.
  3. a.

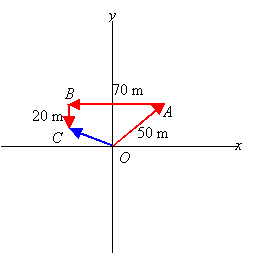
    OC is the net displacement vector.
    b. OC = OA + AB + BC = [(50 m)cos45°i + (50 m)sin45°j] + (-70m)i + (-20 m)j = (-34.6 m)i + (15.4 m)j
    c. |OC| = [(-34.6 m)2 + (15.4 m)2]1/2 = 37.9 m.  
        q = tan-1(15.4 m/-34.6 m) = 24.0°.(north of west)
  4. The vector diagram is as follows:

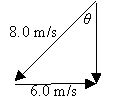
    Find the angle from q = sin-1 (6.0 m/s/8.0 m/s) = 49.0° (south of west).
  5. We choose the coordinate system with +x parallel to the floor down, and +y perpendicular to the floor up.
    Fnet = F1 + F2 + F3  = [(5 N)sin30° + (0 N) - (3 N)]i + [-(5 N)cos30° + (6 N) + (0 n)]j = (-0.5 N)i + (1.67 N)j
    a. The parallel component of the net force is -0.5 N.
    b. The perpendicular component of the net force is 1.67 N.
    c. The magnitude of the net force is F = [(-0.5 N)2 + (1.67 N)2]1/2 = 1.74 N.
        The angle is q = tan-1(1.67 N/-0.5 N) = 73.3° ( below the floor), or 16.7° to the horizontal.

    6.