CHAPTER 5

  1. a. The free-body diagram for the piano is as shown.

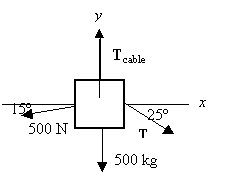
    As the piano is moving steadily, we have
    SFx = Tcos25° - (500 N)cos15° = 0, which gives T = 533 N.
    b. SFx = Tcable - (500 kg)(9.8m/s2) - (500 N)sin15° - (533 N)sin25° = 0, which gives Tcable = 5.26 x 103 N.
  2. We find the ball's acceleration in the tube.
    F = ma;
    2.0 N = (0.050kg)a, a = 40 m/s2.
    We find the velocity of the ball on the top of the tube.
    v2 = v02 + 2ay = 0 + 2(40 m/s2)(1.0 m) = 80 m2/s2, v = 8.94 m/s.
    We find the distance the ball go high in the air from the top of the tube.
    v2 = v02 - 2ay;
    0 = (8.94 m/s)2 - 2 (9.8m/s2)y, y = 4.44 m.
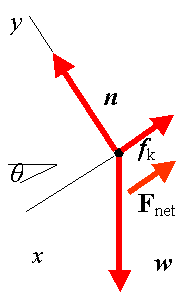
  3. We draw the free-body diagram for Johnny.
     Choose the coordinate system as shown.
      SFx = -f + mgsinq = max. 
      SFy = n - mgcosq  = 0.
      We have f = mn = mmgcosq , substitute f into x-equation to find ax.
       ax = mg(sinq  - mkcosq)/m = g(sinq  - mkcosq) 
           = (9.8m/s2)[sin20° - (0.5)cos20°] = -1.25m/s2.
    Find the initial speed from
      v2 = v02 + 2 axx;
      0 = v02 + 2 (-1.25m/s2)(3.5 m), v0 = 2.96m/s.    		  
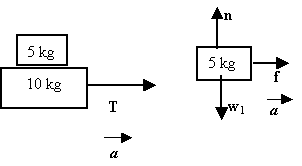
  4.  To prevent the wood box sliding, the friction force between the box and sled holds the box and the sled moving together with the same acceleration.
    We draw the free-body diagrams for sled and the box as shown.
     For the sled and box:
       T = (m1 + m2)a, a = T/(m1 + m2)
    For the box:
       SFx = f = mkn = m1a;
       SFy = n - w1 = 0, n = w1 =  m1g,
    So f = mkm1g.
    To prevent the box from sliding,  f  =  mkm1g > m1a = m1T/(m1 + m2),
    Or T < (m1 + m2)mkg = (5 kg + 10 kg)(9.8m/s2)(0.2) = 29.4 N.     		  
  5. The free-body is as shown.
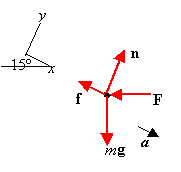
     We choose the coordinate system as shown.
       SFx = -f  - Fcosq  + mgsinq = max. 
       SFy = n - mgcosq  = 0.
    So, ax = [mgsinq - mkmgcosq - Fcosq]/m
               = [(75 kg)(9.8m/s2)sin15° - mk(75 kg)(9.8m/s2)cos15° - (50 N)cos15°]/(75 kg) > 0.
    When  ax = 0,  mk = 0.19992. so the best wax is green with mk = 0.15 < 0.19992.