CHAPTER 6

  1. From the graphs we find the components of accelerations in x-direction as
    ax = [(10m/s) - 0]/[(2 s) - 0] = 5 m/s2, from t = 0 to t = 2 s, and ax = 0 from t = 2 s to t = 4 s.. 
    In the y-direction ay = constant.
    a. We find the time 
        From t = 0  to t = 2 s:  x = x0 + vx0t + 1/2ax(2 s)2,
        from t = 2s to t = t s: x = (10 m/s)(t - 2 s)
       20 m = 0 + 0 + 1/2(5 m/s2)(2 s)2 + (10 m/s)(t - 2 s), solving the equation we have t = 3 s.
    b. We find ay from
       y = y0 + vy0t + 1/2ayt2,
       0 = 9.0 m + 0 + 1/2ay( 3 s)2, ay = -2 m/s2.
      v4y = 0 + (-2 m/s2)(4 s ) = -8 m/s.
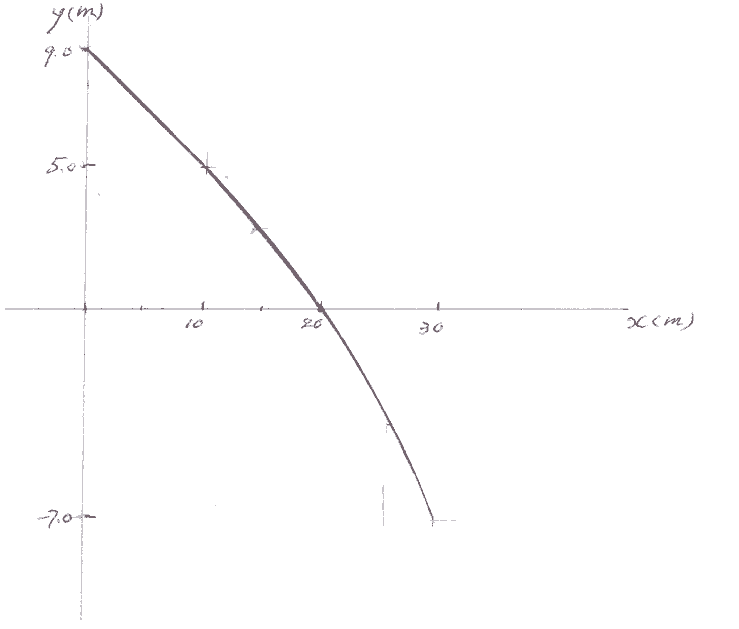
    c. From t = 0 to t =2 s, we have x = 1/2(5 m/s2)t2, and y = 9.0 m + 1/2( -2 m/s2)t2; eliminating t, we have y = (9.0 -0.4x)
       From t = 2 s and later, we have x = 10 m + (10 m/s)(t - 2 s), and y = 9.0 m + 1/2( -2 m/s2)t2
      Eliminating t we have
      y = 8- 0.2 x - 0.01x2
  2. a. The sailor and the spyglass are both in the same inertia reference frame, i.e., the ship; the motion of the spyglass is free fall in the ship. So, the spyglass lands on the base of the mast.
    b. Relative to the fisherman, the motion of the spyglass is projectile motion with v0 = 4.0 m/s and q0 = 0?. Find the range of the projectile motion.
        Find the time that the spyglass lands.
         y = 1/2gt2
        15 m = 1/2(9.8m/s2)t2, which gives t = 1.75 s.
       Find the range.
        x = vxt = (4.0 m/s)(1.75s) = 7.00m.
  3. a. We find the height of the cliff.
        h = y0 + vy0t - 1/2gt2;
          = 0 + (30 m/s)(sin60º)(4.0 s) - 1/2(9.8m/s2)(4.0 s)2
          = 25.5 m.
    b. Find the maximum height of the ball.
        v2 = v02 - 2gy;
        0 = [(30 m/s)(sin60?)]2 - 2(9.8m/s2)ymax,  ymax = 34.3 m.
    c. Find the impact speed.
        vy = (30 m/s)sin60º -(9.8 m/s2)(4.0 s) = -13.2 m/s (down), and vx = (30 m/s)cos60º = 15 m/s.
        v = [vx2 + vy2]1/2 = [(-13.2 m/s)2 + (15 m/s)2]1/2 = 20.0 m/s.
  4. We find the time to hit the plane.
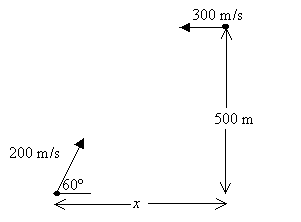
     y =  y0 + vy0t - 1/2gt2;
    500 m = 0 + (200 m/s)sin60?t - 1/2(9.8m/s2)t2, t = 3.17s, 32.1 s.
    The horizontal speed of the shell with respect to the plane is v = (200 m/s)cos60? + 300 m/s = 400 m/s.
    x1 = vxt = (400 m/s)(3.17 s) = 1.267 km.
    x2 = vxt = (400 m/s)(32.1 s) = 12.84 km..
    We get two answers: 1.267km when the plane is closer (shell ascends), and 12.84 km when the plane is farther away. (shell descends)
  5. a. We have v = vboat + vwind
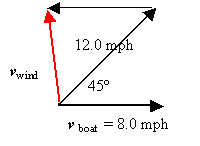
        vwind = v - vboat.
        vwind, = [(12.0 mph)cos45? - (8.0 mph)]i + [(12.0 mph)sin45? - 0]j
                  = (0.49 mph)i + (8.5 mph)j
        vwind = [(0.49 mph)2 + (8.5 mph)2]1/2 = 8.51 mph
        q = tan-1(85.1 mph/0.49 mph) = 86.7? (northwest)
          
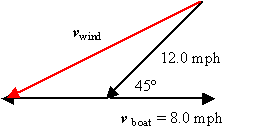
    b. vwind = v - vboat.
        vwind, = [(-12.0 mph)cos45? - (8.0 mph)]i - [(12.0 mph)sin45? - 0]j
                  = (-16.5 mph)i - (8.5 mph)j
        vwind = [(-16.5 mph)2 + (8.5 mph)2]1/2 = 18.6 mph
        q = tan-1(8.5  mph/16.5 mph) = 27.3? (northeast)
  6. Find the time from the range of the cat's motion.
    R = vcat02sin2q0/g = vcat0cosq0t;
    (4.0 m/s)2sin2(30?)/(9.8m/s2) = (4.0 m/s)cos30?t, t = 0.41 s.
    Find the distance.
    d = vcat0cosq0t - vmouset = (4.0 m/s)cos30?(0.41 s) - (1.5 m/s)(0.41 s) = 0.81m.