CHAPTER 7

1. The static friction between the car and the road serves as the centripetal force.
    f = F_r = mv²/r = (1500 kg)(15 m/s)²/(50 m) = 6.75 x 10³ N.
2. Draw the free-body diagram for the ball as shown.
        
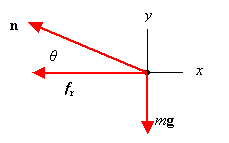
   ΣF_y = nsinθ - mg = 0, n = mg/sinθ
   f_r = ncosθ = mgcosθ/sinθ.
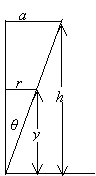
   In the cone, we have sinθ = (a² + h²)^1/2, and cosθ = h/(a² + h²)^1/2.
   Find the radius r of the ball's circular motion from r = ysinθ = ay/(a² + h²)^1/2 .
   f_r = mv²/r.
   v = (f_rr/m)^1/2 = {(mgcosθ/sinθ)(ysinθ)/m]^1/2 = [ghy/(a² + h²)^1/2]^1/2.
3. a. We find the acceleration.
       a = v²/r = (2πr/T)²/r = 4π²r/T² = 4π²(15 m)/(25 s)² = 0.95m/s²
   b. w_app/w = (mg - ma)/mg = (g - a)/g = (9.8 - 0.95)/9.8 = 0.9
   c. w_app/w = (mg + ma)/mg = (g + a)/g = (9.8 + 0.95)/9.8 = 1.1.
4. a. The tangential force is F_t = Fsinθ = (3.5 N)sin70° = 3.29 N.
        a_t = F_t/m = (3.29 N)/(0.5 kg) = 6.58 m/s²
        a_r = a_t/r = (6.58 m/s²)/(2.0 m) = 3.29 rad/s²
       Find time Δt.
        θ_f= θ₀ + ω₀Δt + a_r/2(Δt)²;
       (10 rev)(2π rad/rev) = 0 + 0 + (3.29rad/s²)/2(Δt)², Δt = 6.2 s.
       ω = ω₀ + a_rΔt = 0 + (3.29rad/s²)(6.2 s) = 20.3 rad/s
   b. At Δt = 6.2 s, v_t = ωr = (20.3 rad/s)(2.0 m) = 40.6 m/s.
       Find tension.
       F_t = mv_t²/r + Fcosθ = (0.5 kg)(40.6 m/s)²/(2.0 m) + (3.5N)cos70° = 413 N.
5. At the top of the swing the tension in the string is zero. Find the speed at the top of the swing.
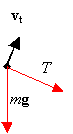
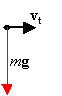
       mg = mv_t²/r, v_t = Ögr = (9.8 m/s²)(0.5 m) = 2.21 m/s.
   When the string is released at the top of the swing the ball moves as a projectile motion with v_x0 = v₀ = 2.21 m/s and v_y0 = 0.
   Find the time of projectile motion from vertical motion.
      y = y₀ + v_y0 t + 1/2gt²;
     (.5 m + 1.5 m) = 0 + 0 + 1/2(9.8m/s²)t², t = 0.64 s.
   Find the horizontal distance.
     x = v_xt = (2.21 m/s)(0.64 s) =1.41 m.