CHAPTER 9

1. a. Impulse = J_x = area under F(x) between t = 0 s to t = 30 s.
         J_x = 1/2(1000 N)((30 s) = 1.5 x 10⁴ N·s
   b. At t = 30 s the rocket reaches its maximum speed.
      Use impulse-momentum theorem
     Dp = mv_max,x - mv_ix = J_x;
    (425 kg)[v_max,x - (75 m/s) = 1.5 x 10⁴ N·s,  v_max,x = 111.3 m./s
2. Use conservation of momentum to find the speed of the four-car train immediately after they couple.
    3mv_3i + mv_1i = 4mv_4i;
   3(2.0 m/s) + (4.0 m/s) = 4v_4i,  v_4i = 2.5 m/s
   Again from conservation of momentum
   4mv_4i + mv_1i = 5mv_5i;
   4(2.5 m/s) + 0 = 5v_5i, v_5i = 2.0 m/s.
3. Take the coordinate system with east as +x-direction and north as +y-direction.
   From conservation of momentum
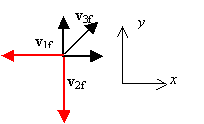
   x-direction: Mv_ix = m₁v_1fx +  m₂v_1fx + m₃v_3fx; 0 = m(-20 m/s) + m(0) + 2mv_3fx, v_3fx = +10 m/s.
   y-direction: Mv_iy = m₁v_1fy +  m₂v_1fy + m₃v_3fy; 0 = m(0) + m(-20 m/s) + 2mv_3fy, v_3fy = +10 m/s
   v_3f = (v_3fx² + v_3fx²)^1/2 = [(-10 m/s )²+(-10 m/s)²]^1/2 = 14.14 m/s.
   θ = tan^-1(v_3fy/(v_3fx) = tan^-1[(-10 m/s)/(-10m/s)] = 45°.
   The speed of the third piece is 14.14 m/s north of east.
   
4.  Find the speed of the bullet when it passes through the first block.
   m_bulletv_bullet,i + m_block1v_block1,i = m_bulletv_bullet,f + m_block1v_block1,f;
   (0.01 kg)(400 m/s) + 0 = (0.01 kg)v_bullet,f + (0.5 kg)(6.0 m/s), v_bullet,f = 100 m/s.
   Find the speed of the bullet when it stops.
   m_bulletv_bullet,i + m_block1v_block2,i = m_{block2+bullet}v_block2,f, 
   (0.01 kg)(100 m/s) + 0 = (0.5 kg + 0.01 kg)v_block2,f, v_block2,f = 1.96 m/s.
5. Find the shell's speed (horizontal only) at the highest point before the explosion.
   v_xi = v₀cosθ₀ = (125 m/s)cos 55° = 72.7 m/s
   As the explosion exerts horizontal force only, the initial speed of the heavier fragment is zero and the lighter fragment has horizontal component only after the explosion.
   Find the speed of the lighter fragment immediately after the explosion.
   Mv_xi = m₁v_1xf+ m₂v2_xi
   (75 kg)(72.7 m/s) = 1/5(75 kg)v_1xf + 4/5(75 kg)(0),
   v_1xf  = 358.5 m/s.
   Find the height of the shell when it explodes.
   v_y² = v_y0² - 2gh, 
   0 = (125 m/s)sin55°]² - (9.8 m/s²)h, h = 535 m.
   Find the horizontal distance of the explosion point to the launch point.
   x₁ = 1/2R = 1/2v₀²sinθ₀/g =1/2(125 m/s)²sin110°/(9.8 m/s²) = 749 m.
   Find the time the lighter fragment in the air.
   h = 1/2gt²;
   (535 m) = 1/2((9.8 m/s²)t², t = 10.4 s
   Find the distance of the lighter fragment it lands from the explosion point.
   x₂ = v_1xft = (358.5 m/s)(10.4 s) = 3.73 x 10³ m
   x = x₁ + x₂ = 749 m + 3.73 x 10³ m = 4.5 x 10³ m