CHAPTER 13 HOMEWORK
1. (p.356 Ex. 5) A bottle has a mass of 35.00g when empty and 98.44g when filled with water. When filled with another fluid, the mass is 88.78g. What is the specific gravity of this other fluid.
2. (p.356 Ex.11) The maximum gauge pressure in a hydraulic lift is 17.0atm. What is the largest size vehicle (kg) it can lift if the diameter of the output line is 24.5cm?
3. (p.357 Ex.20) A hydraulic press for compacting powdered samples has a large cylinder which is 10.0cm in diameter, and a small cylinder with a diameter of 2.0cm (Fig. 13-48). A lever is attached to the small cylinder as shown. The sample, which is placed on the large cylinder, has an area of 4.0cm2. What is the pressure on the sample if 300N is applied to the lever?
4. (p.357 Ex.34) A scuba diver is diving off the shores of the Cayman Islands. the diver and her gear displace a volume of 65.0L and have a total mass of 63.0kg. (a) What is the buoyant force on the diver? (b) Will the diver sink or float?
5. (p.358 Ex.48) A 6.0-cm-diameter pipe gradually narrows to 4.0cm. When water flows through this pipe at a certain rate, the gauge pressure in these two sections is 32kPa and 24kPa. What is the volume rate of flow?
*6. (p.358 Ex.40) A 3.15-kg piece of wood (SG = 0.50) floats on water. What minimum mass of lead, hung from it by a sting, will cause it to sink?
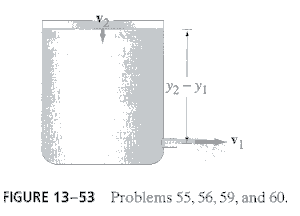
*7. (p.359 Ex.60) (a) I 13-53, show that Bernoulli's principle predicts that the level of the liquid, h = y2 = y1, drops at a rate
dh/dt = -[2ghA12/(A22
- A12 )]
where A1 and A2 are the areas of the opening and the tip surface, respectively, assuming A1 << A2, and viscosity is ignored. (b) Determine h as a function of time by integrating. Let h = h0 at t = 0.(c) How long would it take to empty a 9.4-cm tall cylinder filled with 1.0L of water if the opening is at the bottom and has a 0.50-cm diameter?
