CHAPTER 4 HOMEWORK
1. (P.99 Ex.9) Superman must stop a 100-km/h train in 150m to keep it from hitting a stalled car on the tracks. If the train's mass is 3.6 x 105kg, how much force must he exert? Compare to the weight of the train.
2. (p.99 Ex.14) How much tension must a rope withstand if it is used to accelerate a 1200-kg car vertically upward at 0.80m/s2?
3. (p.99 Ex.21) A Saturn V rocket has a mass of 2.75 x 106kg and exert a force of 33 x106N on the gases it expels. Determine (a) the initial vertical acceleration of the rocket, (b) its velocity after 8.0s, and (c) how long it takes to reach an altitude of 9500m. Ignore the mass of gas expelled (not realistic) and assume g remains constant.
4. (p.100 Ex.34) A 7500-kg helicopter accelerates upward at 0.52m/s2 while lifting a 1200-kg car. (a) What is the lift force exerted by the air on the rotors? (b) What is the tension in the cable (ignore its mass) that connects the car to the helicopter?
5. (p.101 Ex.37) Arlene is to walk across a "high wire" strung horizontally between two buildings 10.0m apart. The sag in the rope when she is at the mid-point should not exceed 10°, as shown in Fig. 4-41. If her mass is 50.0kg, what must be the tension in the rope?
6. (p.101 Ex.40) The block shown in Fig. 4-44 has mass m = 7.0kg and lies on a smooth frictionless plane tilted at an angle q = 22.0° to the horizontal. (a) Determine the acceleration of the block as it slides down the plane. (b) if the block starts from rest 12.0m up the plane from its base, what will be the block's speed when it reaches the bottom of the incline?
7. (p.102 Ex.47) Figure 4-46 shows a block (mass m1) on a smooth horizontal surface, connected by a thin cord that passes over a pulley to a second block (m2), which hangs vertically. (a) Draw a free-body diagram for each block, showing the force of gravity on each, the force (tension) exerted by the cord, and any normal force. (b) Determine formulas for the acceleration of the system and for the tension in the cord. Ignore friction and the masses of the pulley and cord.
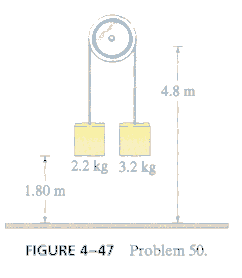
*8. (p.102 Ex.50) The masses shown in Fig 4-47 are each initially 1.80m above the ground, and the massless frictionless pulley is fixed 4.8m above the ground. What maximum height does the lighter object reach after the system is released? [Hint: First determine the acceleration of the lighter mass and then it velocity at the moment the heavier one hits the ground. This is its "launch" speed. Assume it doesn't hit the pulley.]