Chapter 21 HOMEWORK
1. (p.569 Ex.4) What is the repulsive electrical force between two protons in a nucleus that are 5.0 x 10-15m apart from each other?
2. (p.569 Ex.10) Particles of charge +70, +48, and -80mC are placed in a line (Fig. 21-48). The center one is 0.35m from each of the others. Calculate the net force on each charge due to the other two.
3. (P.569 Ex14) At each corner of a square of side l there are point charges of magnitude Q, 2Q, 3Q, and 4Q(Fig 21-49). Determine the force on each charge due to the other three charges.
4. (p.570 Ex.38) Calculate the electric field at the center of a square 52.5cm on a side if one corner is occupied by a +45.0mC charges.
5. (p.571 Ex.42) Two parallel circular rings of radius R have their centers on the x axis separated by a distance l as shown in Fig 21-55. If each ring carries a uniformly distributed charge Q, find the electric field, E(x), at points along the x axis.
6. (p.571 Ex.55) An electron has an initial velocity vo = 8.0 x 104m/si. It enters a region where E = (2.0i + 8.0j) x 104N/C. (a) Determine the vector acceleration of the electron as a function of time. (b) At what angle q is it moving (relative to its initial direction ) at t = 1.0ns?
7. (p.572 Ex.61) The HCL molecule has a dipole moment of about 3.4 x 10-30C.m. The two atoms are separated by about 1.0 x 10-10m. (a) What is the net charge on each atom? (b) Is this equal to an integral multiple of e? If not, explain. (c) What maximum torque would this dipole experience in a 2.5 x 104N/c field? (d) How much energy would be needed to rotate one molecule 45° from its equilibrium position of lowest potential energy?
Answer
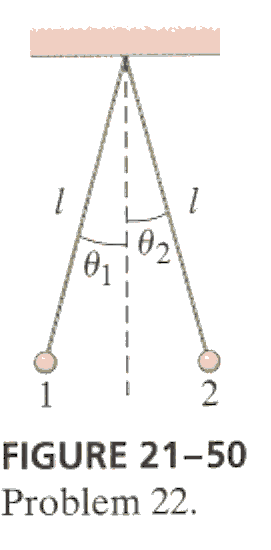
8.* (p.570 Ex.22) Two small charged spheres hang from cords of equal length l as shown in Fig. 21-50 and makes small angles q1 and q2 with the vertical. (a) If Q1= Q, Q2= 2Q, and m1= m2 = m, determine the ratio q1/q2. (b) If Q1 = Q, Q2= 2Q, m1= m, and m2 = 2m, determine the ratio q1/q2. (c) Estimate the distance between the spheres for each other.

9.* (p.570 Ex.23) On each corner of a cube of side l there is a point charge Q. What is the force on the charge at the origin 0 due to the others? (Give answer to vector notation for the charge at the origin in Fig. 21-51.
10.* (p.571 Ex.48) A thin rod of length l carries a total charge Q distributed uniformly along its length. See Fig. 21-56. Determine the electric field along the axis of the rod starting at one end--that is, find E(x) for x >0 in Fig. 21-56.
Answer.
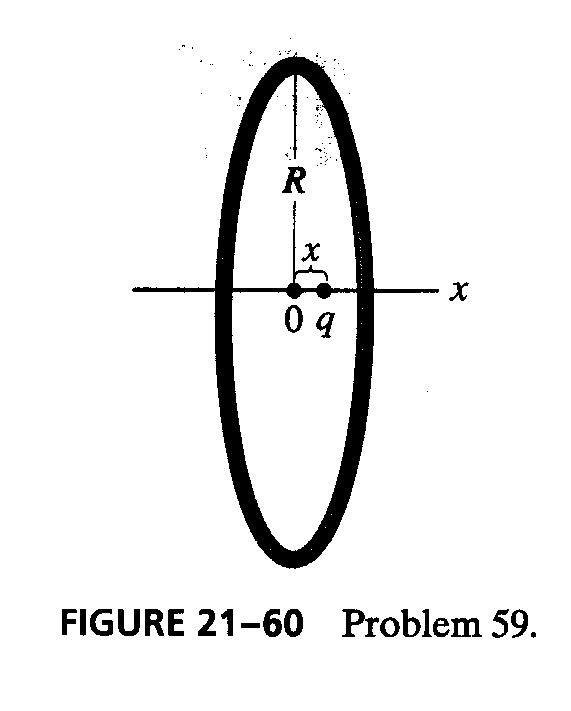
11* (p.572 Ex.59) A positive charge q is placed at the center of a circular ring of radius R. the ring carries a uniformly distributed negative charge of total magnitude -Q. (a) If the charge q is displaced from the center a small distance x as shown in Fig. 21-60, show that it will undergo simple harmonic motion when released. (b) If its mass is m, what is its period?
12.* (P.572 Ex. 64) Suppose a dipole p is placed in a nonuiform electric field E = Ei that points along the x axis. If E depends only on x. Show that the net force on the dipole is
F = (p · dE/dx)i,
where dE/dx is the gradient of the field in the x direction.