CHAPTER 23 HOMEWORK
1. (p.608 Ex.5) The work done by an external force to move a -8.10mC charge from point a to point b is 8.00 x 10-4J. If the charge was started from rest and had 2.10 x 10-4J of kinetic energy when it reached point b, what must be the potential difference between a and b?
2. (p.608 Ex.11) A uniform electric field E = -300N/Ci points in the negative <x direction as shown in Fig 23-22. The x and y coordinates of points A, B, and C are given on the diagram (in meters). Determine the differences in potential (a) VBA, (b) VCB, (c) VCA.
3. (p.608 Ex.16) Determine the difference in potential between two points that are distances Ra and Rb from a very long (>>Ra or Rb) straight wire carrying a uniform charge per nit length l.
4. (p.609 Ex.23) A +25-mC charge is placed 6.0cm from an identical +25-mC charge. How much work would be required by an external force to move a +0.10-mC test charge from a point midway between them to a point 1.0cm closer to either of the charges?
5. (p.609 Ex.31) A flat ring of inner radius R1 and outer radius R2, Fig. 23-27, carries a uniform surface charge density s. Determine the electric potential at points along the axis (the x axis).
6. (p.609 Ex.36) Draw a conductor in the shape of a football. This conductor carries a net negative charge, -Q. Draw in a dozen or so electric field lines and equipotential lines.
7. (p.610 Ex.41) (a) In Example 23-10 part b, calculate the electric potential without using the dipole approximation, Eq. 23-7; that is don't assume r >> l. (b) What is the percent error in this case when the dipole approximation is used?
8. (p.610 Ex.55) An electron starting from rest acquires 2.0keV of kinetic energy in moving from point A to point B. (a) How much kinetic energy would a proton acquire, starting from rest at B and moving to point A? (b) Determine the ratio of their speeds at the end of their respective trajectories.
9.* (p.608 Ex.19) A very long conducting cylinder (length L) of radius R0 (R0 << L) carries a uniform surface charge density s (C/m2). The cylinder is at an electric potential V0. What is the potential at points far from the end, at a distance r from the center of the cylinder? Determine for (a) r > R0 and (b) r < R0. (c) Is V = 0 at r = ¥ (assume L = ¥)? Explain.
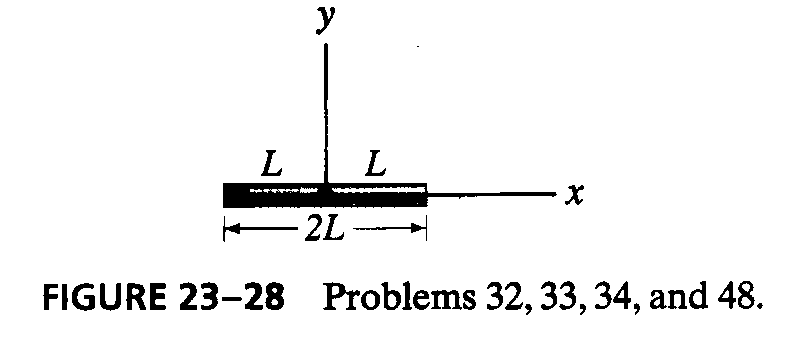
10*. (p.609 Ex34) The charge on the rod of Fig. 23-28 has a nonuniform linear charge distribution, l = ax. Determine the potential V for (a) points along the y axis and (b) points along the x axis outside the rod.

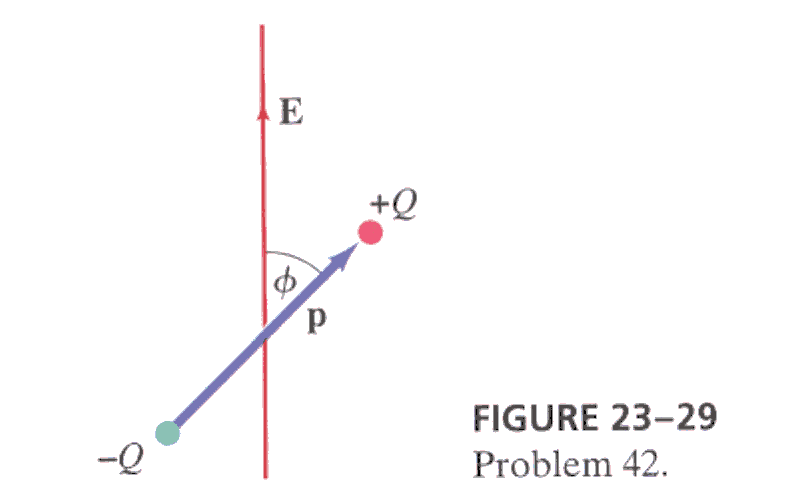
11*. (p.610 x.42) Show that if an electric dipole is placed in a uniform electric field, then a torque is exerted on it equal to pEsinf, where f is the angle between the dipole moment vector and the direction of the electric field as shown in Fig. 23-29. What is the net force on the dipole? How are your answers affected if the field is nonuniform? Note that the dipole moment vector p is defined so that its magnitude is Ql and its direction is pointing from the negative end to the positive end as shown.
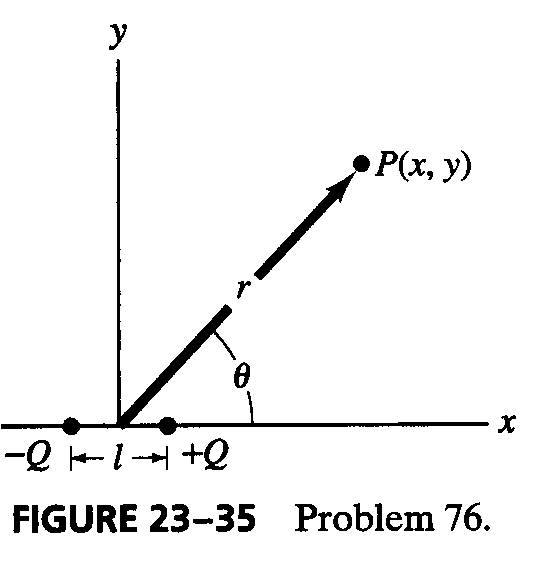
12*. (p.612 Ex.76) Determine the components of the electric field, E and E, at any point point P in the xy plane due to a dipole, Fig. 23-35, starting with Eq. 23-7. Assume r = (x2+ y2)1/2 >> l.