CHAPTER 28 HOMEWORK
1. (p.728 Ex.7) Two long thin parallel wires 15.0cm apart carry 25-A currents in the same direction. Determine the magnetic field strength at a point 12.0cm from one wire and 5.0cm from the other (Fig. 28-30).
2. (p.729 Ex.15) Let two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wire is at x =0, the other at x = d, Fig. 28-33. Determine B between the wires as a function of x.
3. (p.730 Ex.25) A 20.0m long copper wire, 2.00mm in diameter including insulation, is tightly wrapped in a single layer with adjacent coils touching, to form a solenoid of diameter 2.50cm. What is (a) the length of the solenoid and (b) the field at the center when the current in the wire is 20.0A?
4. (p.730 Ex.30) A wire, in a plane, has the shape shown in Fig. 28-37, two arcs of a circle connected by radial lengths of wire. Determine B at point C in terms of R1, R2, q, and the current I.
5. (p.731 Ex.36) Consider a straight section of wire of length l, as in Fig. 28-42. which carries a current I. (a) Show that the magnetic field at a point P a distance R from the wire along its perpendicular bisector is
B = (moI/2pR)[l/(l2 + 4R2)1/2].
(b) Show that this is consistent with Example 28-9 for an infinite wire.
6*. (p.729 Ex.19) Avery long flat conducting strip of width L and negligible thickness lies in a horizontal plane and carries a uniform current I across its cross section. (a) Show that at points a distance y directly above its center, the field is given by
B = (moI/pL)tan-1(L/2y),
assuming the strip is infinitely long. [Hint: Divide the strip into many thin "wires," and sum (integrate) over these.] (b) What value does B approach for y >> L? Does this make sense? Explain.
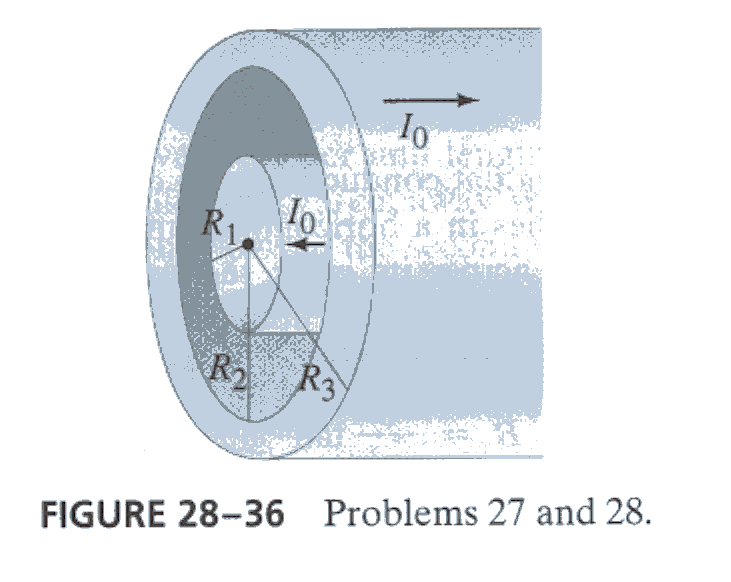
7*. (p.730. Ex.28) Suppose the current in the coaxial cable of Problem 27, Fig. 28-36, is not uniformly distributed, but instead the current density j varies linearly with distance from the center: j1 = C1R for the inner conductor and j2 = C2R for the outer conductor. Each conductor still carries the same total current I0, in opposite directions. Determine the magnetic field in terms of I0 in the same four regions of space as in Problem 27.

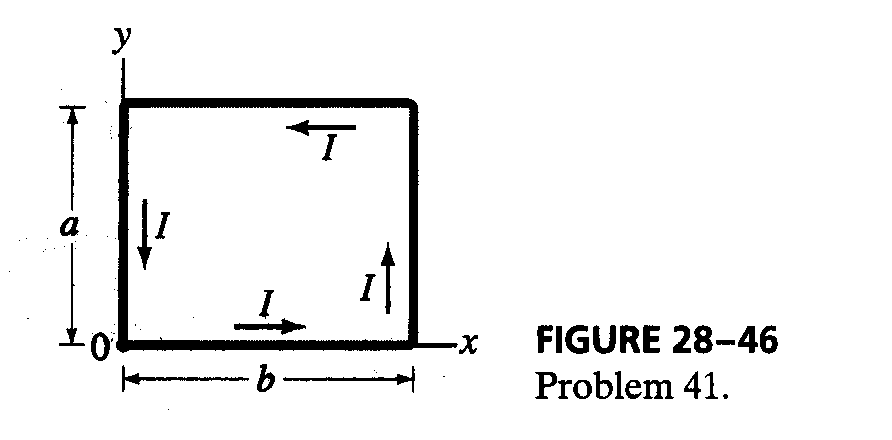
8*. (p.731 Ex.41) A single rectangular loop of wire, with sides a and b, carries a current I. An xy coordinate system has its origin at the lower left corner of the rectangle with the x axis parallel to side b (Fig. 28-46). Determine the magnetic field B at all points (x, y) within the loop.