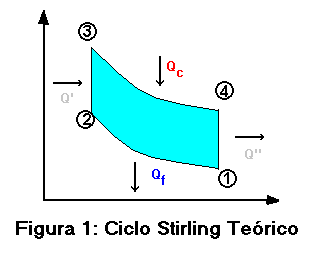
Detalle del ciclo Stirling.

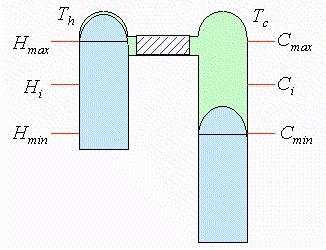	En 1 el cilindro frío está a máximo volumen y el cilindro caliente está a volumen mínimo, pegado al regenerador. El regenerador se supone está "cargado" de calor
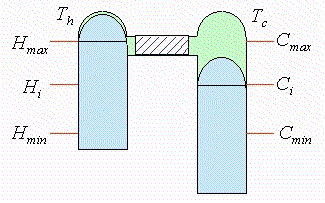	Entre 1 y 2 se extrae la cantidad Qf de calor del cilindro (por el lado frío). El proceso se realiza a Tc constante. Por lo tanto al final (en 2) se estará a volumen mínimo, Vmin, Tc y p2. El pistón de la zona caliente no se ha desplazado. En esta evolución es sistema absorbe trabajo.
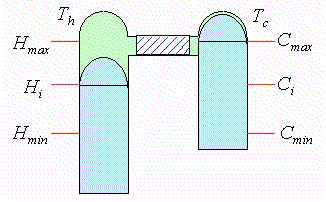	Entre 2 y 3 los dos pistones se desplazan en forma paralela. Esto hace que todo el fluido atraviese el regenerador. Al ocurrir esto, el fluido absorbe la cantidad Q' de calor y eleva su temperatura de Tc a Th. Por lo tanto al final (en 3) se estará a Th, Vmin y p3. El regenerador queda "descargado". En esta evolución el trabajo neto absorbido es cero (salvo por pérdidas por roce al atravesar el fluido el regenerador).
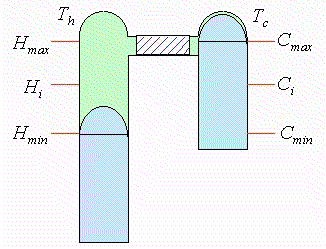	Entre 3 y 4 el pistón frío queda junto al lado frío del regenerador y el caliente sigue desplazándose hacia un mayor volumen. Se absorbe la cantidad de calor Qc y el proceso es (idealmente) isotérmico. Al final el fluido de trabajo está a Th, el volumen es Vmax y la presión es p4.
	Finalmente los dos pistones se desplazan en forma paralela de 4 a 1, haciendo atravesar el fluido de trabajo al regenerador. Al ocurrir esto el fluido cede calor al regenerador, este se carga de calor, la temperatura del fluido baja de Th a Tc y la presión baja de p4 a p1. Al final de la evolución el fluido está a Vmax, p1 y Tc. El regenerador sigue "cargado" de calor.

Haz click en la imagen para ver el "avi" con el ciclo en funcionamiento...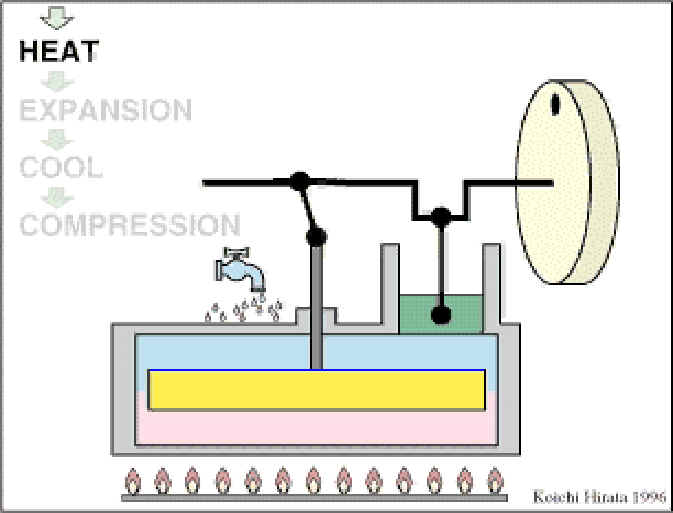

Teóricamente el gas utilizado en el ciclo cerrado es ideal, por lo que utilizando el segundo principio de la termodinámica nos da u rendimiento teórico:

n = 1 - q_ced/Q_abs

Y utilizando los calores cedidos y recibidos nombrados mostrados en el gráfico nos da:

como Q' = -Q'' se tiene que:

n = (Q_h - Q_c)/(Q_h + Q')

como se señaló antes, el modelo teórico nos dice que el regenerador del motor es de una eficiencia del 100% por lo que se necesita sólo un calor inicial para comenzar el ciclo, ya que después este calor se recupera; por lo que el resultado es:

Del gráfico de desprende que:

-Q_f = R'T_f ln(p₁/p₂) y Q_c = R'T_c ln(p₄/p₃)

ya sabemos que (p₄/p₃) = (p₁/p₂)

Reemplazando en la ecuación de eficiencia:

n = 1 - T_f/T_c , que es el rendimiento de Carnot.