INTERACCION ENTRE UNA EMULSIÓN

Y UNA SUPERFICIE SÓLIDA

Lic. Ernesto Carrizo

(FCE y N - UBA 1963)

-Asesor Técnico de Hispano Química Argentina S.A.

-Profesor Titular de Físico Química y Termodinámica (UTN)

-Profesor Titular de Físico Química (UNLU)

-Profesor Adjunto de Química Física (Fac. Ingeniería, UBA)

-Profesor del Centro Argentino de Tribología (Cámara Arg. de Lubricantes)

Ariel N. Santanera

(Técnico Químico - EINILAH)

-Gerente Técnico de Hispano Química Argentina, S.A.

-Profesor del Centro Argentino de Tribología (Cámara Arg. de Lubricantes)

Buenos Aires, 1991.

1 - INTRODUCCION

La lubricación mediante emulsiones es una práctica antiquísima, especialmente en operaciones de mecanizado y de deformación plástica.

Hay una tendencia a considerar a las emulsiones lubricantes y refrigerantes simplemente como fluidos de propiedades intermedias entre las del agua y las del aceite.

Aunque desde un enfoque macroscópico esto pueda tener alguna apariencia de verdad, la realidad es muy diferente a poco que hagamos una consideración microscópica, especialmente prestando atención a las interfases que pueden estar involucradas. También funcionalmente aparecen comportamientos específicos atribuibles a las interacciones dentro de su estructura particular.

Dejando de lado el caso de las emulsiones Inversas, en las emulsiones de aceite en agua en contacto con una superficie metálica podemos imaginar diversas situaciones:

a) La superficie metálica está totalmente mojada por la fase acuosa, y la fase oleosa está dispersa en la fase acuosa sin hacer contacto con el metal.

b) La superficie metálica está totalmente mojada con una película de la fase oleosa. El resto de la fase oleosa permanece dispersa en la acuosa.

c) La superficie metálica está parcialmente en contacto con la fase acuosa, parcial mente en contacto con la oleosa.

Podría tratarse de una situación dinámica, en la cual la fase oleosa se adhiere y se desprende sucesivamente de la superficie metálica.

Para determinar cuál es la situación que realmente se produce en un caso dado, se hace fundamental estudiar el comportamiento de una gota de fase oleosa, suspendida en la fase acuosa, que hace contacto cuasi tangencial con la fase sólida. En un esquema:

(utilizando la nomenclatura tradicional: 0 = fase aceite W = fase acuosa M = fase metal)

¿Es una situación de equilibrio, y por lo tanto estática?

¿0 es una situación dinámica? En este caso: ¿Se moverá la gota hacia mojar una mayor superficie metálica, o hacia desprenderse de ella y reincorporarse a la fase acuosa?

Para dar respuesta a estas preguntas, es decir, para describir el comportamiento de la gota emulsionada, podemos intentar diversos enfoques:

Mecánico: Teniendo en cuenta las fuerzas resultantes de las tensiones interfasiales, y ángulos de contacto.

Termodinámico: Teniendo en cuenta los cambios de energía libre al crearse y destruirse Interfases.

Estos dos caminos, que han sido extensivamente desarrollados, dejan de ser útiles cuando se toman en cuenta las reales estructuras microscópicas de las Interfases que, inclusive en la actualidad, no se conocen en detalle. Su estudio experimental presenta grandes dificultades, especialmente en el caso de las emulsiones.

Enfoque teórico básico: Estudia modelizando en forma muy detallada las estructuras de las diferentes fases e Interfases en juego. Si bien este camino es el correcto, pues procura representar fielmente la realidad fisicoquímica, no ha llegado todavía a conclusiones definitivas y por lo tanto resulta por ahora de poca aplicación tecnológica.

Nos propusimos entonces desarrollar un modelo simplificado de las emulsiones que tuviese aplicación tecnológica casi inmediata.

Para hacernos una idea de las dificultades que se encuentran al intentar modelar la morfología y las interacciones dentro del sistema "emulsión en contacto con una superficie metálica", podemos observar este croquis:

En él hemos esquematizado (utilizando la nomenclatura tradicional):

- La fase metal (M)

- La fase contínua, acuosa (W)

- La fase dispersa, oleosa (0). Esta fase oleosa puede también estar en contacto con la fase metal, no solamente formando gotas rodeadas de la acuosa.

- Las posiciones de las moléculas del tensioactivo:

Una parte importante de las moléculas de tensioactivo han de ubicarse en la interfase O / W. La parte hidrófila se orientará hacia el agua, la parte hidrófoba hacia el aceite. Como resultado, obtendremos una capa molecular ordenada, en rigor un cristal liquido (ver detalle 1). También es factible que esta capa no sea de espesor monomolecular, sino que esté formada, por ejemplo, por tres subcapas (ver 2). Una u otra configuración podrían estar determinadas por la concentración del tensioactivo en el sistema.

Otras moléculas del tensioactivo estarán ubicadas en el interior de las fases (ver 3 y 4). Según sea el HLB ("balance hidrófilo - lipófilo del tensioactivo) será más factible encontrarlas en el agua o en el aceite. Estas moléculas, en el interior de las fases, podrían también formar miscelas. Esta posibilidad depende de que la concentración en la fase sobrepase la concentración miscelar crítica. Esta concentración es conocida en el caso de soluciones (fases únicas) en las cuales las interfases son despreciables. Pero no parece tan fácil de estudiar en el caso de emulsiones, donde, según dijimos, una parte importante del tensioactivo se ubicará en una interfase muy extensa. (ver detalles 5 y 6).

¿Qué pasará en las interfases W/M y O/M? ¿Formará capas el tensioactivo? (ver 8)

Se ha estudiado (HLB) la afinidad hacía el agua y hacia el aceite de los tensioactivos. Pero en pocos casos conocemos la afinidad comparativa hacia la superficie metálica.

2 - MODELO 1

Consideremos un sistema extremadamente simplificado: una gota de aceite emulsionada en agua gracias a un tensioactivo tipo soluble.

Es posible deducir una ecuación que relacione el radio de la gota con la concentración del tensioactivo.

Definamos: VT = volumen total de la gota.

VO = volumen interior de la gota (oleosa).

Vi = volumen de la interfase.

H = hidrofilidad de la molécula tensioactiva, = f(HLB)

VtT = volumen del tensioactivo en el total de la gota.

Vti = volumen del tensioactivo en la interfase.

VtO = volumen del tensioactivo en el interior de la gota.

C = concentración del tensioactivo en el total de la gota.

Ci = concentración del tensioactivo en la interfase.

Co = concentración del tensioactivo en el interior de la gota.

VT = VO + VI

(1)

l = largo de la molécula

Si consideramos a la interfase como formada por una capa monomolecular ordenada de tensioactivo, entonces:

Suponiendo que la cantidad de tensioactivo (o lo que es lo mismo, su volumen) se reparte en cada zona en proporción a la hidrofilidad:

(2)

Además, de (1):

(3)

Reemplazando (3) en (2) :

Si consideramos que la interfase está formada por tres capas de moléculas, la fórmula pasa a:

Hemos construido juegos de curvas según estas ecuaciones, para diversos valores de H (tensioactivos más o menos hidrófilos) y para diversos valores de Ci (interfase más o menos saturada con el tensioactivo). Pero este análisis simplificado no resulta suficiente para las aplicaciones prácticas.

Avanzando más, procuramos describir un caso más frecuente en la realidad industrial: una fase oleosa que lleva disueltos un emulgente y un aditivo polar, dispersa en una fase acuosa en la cual está disuelto un tensioactivo humectante, que veremos a continuación.

3 - MODELO 2

Este modelo describe la emulsión teniendo en cuenta estos supuestos:

1 - El sistema es una dispersión de una fase oleosa en una fase continua acuosa. Las partículas de la fase dispersa son esféricas, con una cierta distribución de diámetros.

2 - En la fase oleosa, se encuentran presentes moléculas de: a) un tensioactivo (emulgente), molécula polar soluble en aceite, b) un aditivo lubricante, capaz de ser adsorbido por fisisorción o eventualmente quimisorción sobre la fase metal en condiciones de proceso (molécula polar con cierta propiedad tensioactiva). a) y b) son insolubles en agua.

3 - En la fase acuosa se encuentran moléculas de un tensioactivo hidrosoluble, polar.

4 - En la frontera gota/fase contínua se forma una interfase de espesor discreto en la cual se sitúan los excesos interfasiales de los dos tensioactivos y el aditivo según el modelo de Langwuir. (Las moléculas se encuentran con su dimensión mayor perpendicular a la superficie, formando una sola capa).

En la emulsión O / W existe una distribución de tamaño de gotas con diámetro Di, correspondiente a una concentración de gotas por unidad de volumen ni, es decir ni = F(Di), en condiciones fisicoquímicas de composición constante de las fases 0 y W (a T y P constante), existirá una distribución de Di definida. (Fig. 1)

Considerando un volumen VE de emulsión, se cumplirá: VE = Vo + Vw (1)

Con Xo + X _w= 1 siendo Xo, Xw las fracciones volumétricas de cada fase.

y (Observar que % v/v =X₀ . 100)

Ahora: y siendo n= y D un diámetro promedio representativo de la distribución. SI las condiciones de composición de las fases O y/o W cambiaran, n y D también lo harán. Pero para una emulsión dada, Xo = constante y nD3 = constante.

Existen en la bibliografía múltiples formas para definir el valor de D. Por ejemplo en el caso de una sola gota de superficie Sg o volumen Vg y diámetro Dg :

Esto sugiere que para la fase dispersa 0:

y

Lo cual implica para su valuación la medición de la distribución de Di.

De cualquier manera asumimos que en nuestro modelo existe un valor D representativo

de la emulsión, que puede llegar a calcularse por varios métodos.

Si consideramos una gota de la emulsión 0 (fig. 2)

dentro de la fase contínua W, llamamos C al número de molécula por unidad de volumen, al número de moléculas adsorbidas por unidad de superficie y f a la fracción de superficie cubierta por el adsorbato considerado; L es la longitud promedio representativa de las moléculas adsorbidas, el aditivo lubricante 0, y los tensioactivos 0 y W; Cjo. es la concentración de la sustancia j en el seno del volumen libre Ve excluyendo el volumen superficial "ocupado" por las moléculas adsorbidas; Cww es la concentración del tensioactivo W en el seno de la fase contínua W. Buscamos D=F(Co, Ct, Cwe, Xo, Constantes físicas).

Tendremos:

, fo + fT + fw = 1 (1)

Realizando un balance de moléculas 0 y T en la gota:

Aditivo O : (2)

Tensioactivo T : 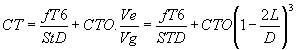(3)

Suponemos que el volumen de cada molécula adsorbida Vj = Sj . Lj siendo Sj la sección de adsorción y Lj su longitud efectiva.

El balance de moléculas W en el sistema E es el siguiente:

(4)

Los parámetros D y f están interrelacionados entre, sí; suponiendo que Co, CL y Cwe son

valores pequeños, podemos aceptar que los Esta es una expresión del tipo Henry o

Langmuir simplificada donde Kj es una constante propia de cada sustancia adsorbida en la

interfase. Por lo tanto para la interfase i podemos plantear:

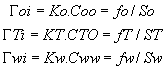(5)

Reemplazando (5) en (4) (3) y (2), tenemos:

(6)

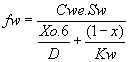
Recordemos que lo que con (6) nos permite resolver el sistema de ecuaciones resultante y obtener D, feo, FTP y f w, siempre que definamos L en forma correcta. En este caso:

L = feo. Lo + ft. LT + fw. Lw (7)

El sistema de 5 ecuaciones resultante dada la no linealidad de (6) sólo puede resolverse programando en computadora. Se consigue una mejor convergencia en la solución si la condición (7) es reemplazada por el valor aproximado:

(8)

Se decidió simular el comportamiento de la emulsión tomando los valores siguientes

de constantes del sistema (según fuentes bibliográficas):

TABLA 1

Se supuso un aceite soluble con g/^cm3 y la emulsión acuosa

Con estos datos, por ejemplo, si el aceite soluble contiene 5% p/p de Ad.O, 10%p/p de tensioactivo T se tiene Co = 0,1389 mol/litro y CT =0,111 mol.

Para la emulsión se tiene con I% p/p de aditivo W, Cwe = 0,0125 mol/litro. Resolviendo el sistema de ecuaciones se obtiene:

D = 950 Amstr. ; fo = 0,195 ; fT = 0,215 ; fw = 0,59 ; D/L = 31

La tabla siguiente muestra la respuesta del modelo propuesto a varias situaciones de formulación y/o proceso:

TABLA 2 - (C en mol/lt, D en Amstrongs)

Los casos 1 a 4 muestran la influencia sobre D de cambios en la formulación del aceite soluble. La presencia de T disminuye el tamaño de gota y es más efectivo que 0, además desplaza al aditivo lubricante de la superficie de la gota.

Los casos 5 a 8 muestran la enorme influencia del tensioactivo en la emulsión para disminuir D y reemplazar al aditivo lubricante en la superficie.

¿Bajo qué condiciones tribológicas fracasa el lubricante? Es difícil decirlo con este modelo teniendo en cuenta que el análisis de fricción o de un proceso industrial, sea de mecanizado o deformación plástica implica condiciones de no equilibrio fisicoquímico; es un caso típico de proceso de no equilibrio con generación de entropía.

Sin embargo, la falta de lubricidad observada en procesos de deformación plástica o mecanizado, al contaminarse la emulsión con tensioactivos o al intentarse aditivar la emulsión, podría deberse a dos efectos simultáneos:

a) disminución de D

b) desplazamiento del aditivo lubricante de la superficie de la gota, lo cual origina un efecto tipo "barrera" para la interacción con la superficie metálica.

Se puede intentar un análisis fisicoquímico usando la isoterma de adsorción de Gíbbs con este modelo de emulsión O/W:

(T = constante) (9)

siendo: j = RT d ln aj y aj = j . cj

es la tensión interfasial, es el potencial químico de la sustancia adsorbida; aj su actividad; j su coeficiente de actividad ; j exceso superficial; y R la constante de los gases ideales.

En este modelo, siendo diluidas las fases en contacto, podemos suponer:

j = 1 y aj = Cj, Con lo que (9) nos queda:

(10)

(kB = constante de Boltzman)

Reemplazando las (5) en (10) e integrando, tenemos:

(11)

donde es la tensión interfasial en ausencia de aditivos.

La ecuación (11) nos indica la relación directa entre la disminución dey la adsorción superficial; si se pudiera medir en forma experimental podría verificarse el éxito del modelo para describir el comportamiento de una emulsión en lo que respecta a variaciones de composición del aceite soluble, y de tencloactivos sobre la emulsión. Por supuesto utilizando datos de simulación por computadora para fo, ft y fm.

4 - CONCLUSIONES

Hasta aquí hemos logrado un modelo que describe cuali y cuantitativamente los cambios que sufre una emulsión como consecuencia de variaciones en las concentraciones de sus componentes, en las características dimensionales de sus moléculas y los coeficientes de distribución entre fase e interfase

.

La tarea siguiente adelantará por tres caminos:

a) comprobación experimental del modelo.

b) perfeccionamiento del modelo, para generalizarlo hasta

donde sea posible,

e) introducción en el modelo de las interacciones con la fase

sólida.

d) Verificación termodinámica del comportamiento del modelo

por simulación con computadora.

5 - BIBLIOGRAFÍA

P. BECHER: "Emulsions, theory & Practics" - Reinhold Publishing Corp. - N.Y. 1965.

P. SHERMAN: "Emulsion Science" - Academic Press - London & N.Y. 1976.

G. L. GAINES, Jr.: "Insoluble monolayers at liquid/gas interfases" - Interscience - N.Y. 1966.

K. K. SEMENCHENKO: "Surface phenomena in metals & alloys" - Pergamon Press - N.Y. - 1961.

N. K. ADAM: "The Physics & Chemistry of Surfaces" - Oxford University Press.

J. LEVINE: "Physical Chemistry" - Mc Graw Hill - 1989.

C. MANS et al.: "La interfase gas-líquido" - Investigación y Ciencia, Nº 136 - Ene 1988.