（３）梁のたわみ　－ヤング率の測定

（３）梁のたわみ　－ヤング率の測定－

実験目的

　両持ち梁の中央に荷重をかけると梁はたわむ。この時、たわみ量は梁の形状とヤング率のよって決まる。従って、たわみ量を測定することによって、その材料のヤング率を知ることができる。このようなヤング率の測定法はユーイング(Ewing)法と呼ばれ、この方法を用いて実際の材料のヤング率を測定することを目的とする。

実験方法

（１）図のように、測定装置のナイフエッジの上に試料棒と補助棒を起き正確な中央に鏡の中足が乗るように“おもりかけ”をつるす。

（２）読みとり望遠鏡をのぞいて、鏡の中の写っている目盛りに焦点を合わせる。この操作を簡単にする方法は最初望遠鏡を通さないで鏡に写っている目盛りを探し、その目の位置へ目盛りを見失わないようにしながら望遠鏡をもってきて望遠鏡の中に目盛りをとらえる。

（３）“おもりかけ”におもりを一つずつ乗せて目盛りを読む。この操作は静かにやらなければ目盛りの揺れが生じて測りにくくなる。

（４）７個のおもりについて全部測定したならば、次におもりを一つずつはずしながら目盛りを読んでいく。そして、全部はずした時に最初の目盛りに戻っているのを確かめる。もし、実験の途中で鏡などがわずかでもずれると、目盛りは元には戻らない。その場合、最初から測定をやり直さなければならない。

（５）寸法測定。厚さ(a)，試料棒の幅(b)，ナイフエッジ間の距離(L)，鏡～目盛間の距離(x)，鏡の前足～後足二本の中央間の距離(z)。

（６）補助棒を新たな試料棒として(3)～(5)をおこなう。

（７）以上のようにして、用意されている三本の試料棒（鋼鉄，真鍮，銅）のヤング率（縦弾性係数）の測定をおこなう。

実験結果と課題

（１）片持ち梁と両持ち梁の“たわみ(e)”を「曲げモーメント」の式から導く。

　たわみ曲線状に微小長さをとり、Ｐ，Ｑにおけるたわみ角をそれぞれ，とすれば、は近似的に円弧とみなされるから、その曲率半径をＲとすると、

　上式の符号は図のようにＰ点が正の方向に進むに従い、角は減少するために用いた。

　上式より、

　Ｐ，Ｑのたわみの差をとして、たわみ角θが小さいならば、

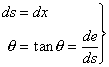
‥‥①

　①式と、曲げモーメントの関係から、

‥‥②

　式②がたわみ曲線を表す微分方程式で、Ｉは中立軸に関する断面二次モーメント，Ｍは中立軸のまわりの曲げモーメントで、ｘの関数として与えられる。

　ただし、は積分定数である。

(a)片持ち梁

　　　であるから、微分方程式は、

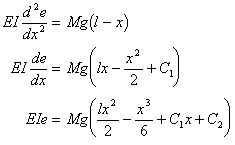
　積分定数は固定端の条件、で，から、

　最大たわみは自由端で生じ、

‥‥③

　式③において、Ｅは材料の種類により、Ｉは断面の形で決まるが、が同じなら、ＥＩが大きいほどたわみｅは小さい。

(b)両持ち梁

　　　図の場合、ＡＣ間　　

　　　　　　　　ＣＢ間　　

　ＡＣ間

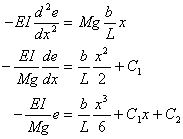
　ＣＢ間

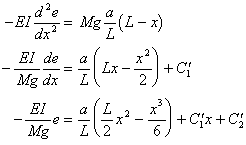
　はつぎの条件から決められる。

　（ⅰ）両支点におけるたわみが０である。

　（ⅱ）荷重点Ｃでは、ＡＣ間，ＣＢ間を別々に計算したたわみ及びたわみ角が等しい。

　（ⅰ）の条件はＡＣ間において、でから

　　　　　　　　ＣＢ間において、でから、

‥‥④

　（ⅱ）の条件は

　　　　　ＡＣ間で、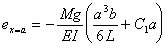

　　　　　ＣＢ間で、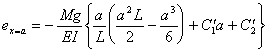

　であるから、

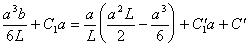‥‥⑤

　また、ＡＣ間で、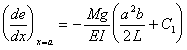

　　　　ＣＢ間で、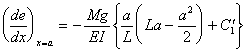

　であるから、

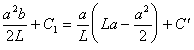‥‥⑥

　式④,⑤,⑥を整理して連立させると、

‥‥⑦

　式⑦をそれぞれＡＣ間・ＣＢ間のたわみの式に代入すると、

　　　ＡＣ間　　‥‥⑧

　　　ＣＢ間　　

　そして、スパン中央のたわみは、式⑧でとおいて、

　さらに、荷重がスパン中央に作用する場合、たわみ曲線は左右対称となり、左側半分に着目して求めればよいことになる。式⑧でとおき、

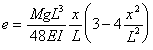
　この場合の最大たわみは、

　となる。

(c)曲げモーメントの証明

上式より、

　力のモーメントより、

　断面全体における力のモーメントは、

‥‥断面二次モーメント

　断面全体における力のモーメントは、断面の形状によって決まることがわかる。

　よって、曲率半径Ｒだけ曲がっているときの曲げモーメント。

（２）光のてこ(Optical Lever)の原理

　鏡Ｍが角度φ回転すると、反射光線の方向は２φ変化する。これを測定するには、スケールＳをＭに写し、その反射像を望遠鏡Ｔで見る。実際は、試料の変位による望遠鏡の十字線の交点の読み（スケールＳ上での）の移動として、読み取ることができる。

　スケールと鏡の間の距離をｘとすると、

　の関係がある。φが小さければ、

‥‥⑨

　となる。

　図は、三脚ＩＪＫに鏡Ｍをつけたもので、これを光りてこと呼ばれる。ＪＫを結んだ線上を軸としてＩが上下に動くとＭは回転する。

　ＩからＪＫまでの垂直距離をｚとすると、

‥‥⑩

　となるので、式⑨,⑩より、

　となる。この式から、小さい変位ｅは()倍に拡大された変位を測定することによって求められる。

（３）測定結果を以下のようにまとめる。

・１回目　　　　　(a=0.0045[m],b=0.01604[m],x=1.620[m])

荷重 [kg]	目盛(増) [mm]	目盛(減) [mm]	平均目盛 [mm]	荷重 [kg]	目盛(増) [mm]	目盛(減) [mm]	平均目盛 [mm]	0.8kgの目盛変化
0	290	290	290	0.8	196	196	196	94.0
0.2	267	267	267	1.0	173	173	173	94.0
0.4	243	243	243	1.2	149	149	149	94.0
0.6	220	219	219.5	1.4	126	126	126	93.5
							平均	93.875

　１回目の寸法測定

・２回目　　　　　(a=0.0045[m],b=0.016[m],x=1.610[m])

荷重 [kg]	目盛(増) [mm]	目盛(減) [mm]	平均目盛 [mm]	荷重 [kg]	目盛(増) [mm]	目盛(減) [mm]	平均目盛 [mm]	0.8kgの目盛変化
0	200	200	200	0.8	153	152	152.5	47.5
0.2	188	188	188	1.0	141	140	140.5	47.5
0.4	176	176	176	1.2	129	129	129	47.0
0.6	165	165	165	1.4	117	117	117	48.0
							平均	47.5

　２回目の寸法測定

・３回目　　　　　(a=0.0045[m],b=0.016[m],x=1.590[m])

荷重 [kg]	目盛(増) [mm]	目盛(減) [mm]	平均目盛 [mm]	荷重 [kg]	目盛(増) [mm]	目盛(減) [mm]	平均目盛 [mm]	0.8kgの目盛変化
0	330	329	329.5	0.8	240	239	239.5	90.0
0.2	308	307	307.5	1.0	218	218	218	89.5
0.4	285	284	284.5	1.2	196	195	195.5	89.0
0.6	263	261	262	1.4	174	174	174	88.0
							平均	89.125

　３回目の寸法測定

・それぞれのヤング率Ｅを求める。

　今回の実験で用いたはりは両持ち梁なので、先ほど求めた両持ちはりの式を用いる。

　ここで、光てこの原理で求まった式を適用して、

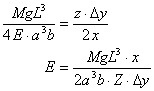
Ｍ=0.8[kg]，ｇ=9.8[m/s²]，Ｌ=0.4[m]，ｚ=0.03[m]

ｘ=スケールと鏡の距離[m]，ａ,ｂ=それぞれの値[m]，Δｙ=目盛の変化の平均値[m]

　上記の値と実験より求まった値を用いて計算すると、

　　　　　１回目

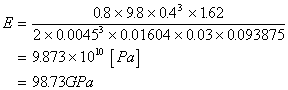
　　　　　２回目

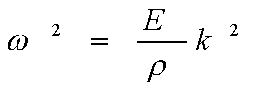
　　　　　３回目

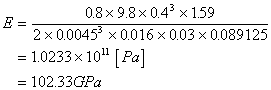
（４）３本の試料棒のヤング率を文献値と比較・考察する。

	実験値	文献値	材質
１回目	98.73GPa	91～96GPa	真鍮
２回目	194.41GPa	203～211GPa	鋼鉄
３回目	102.33GPa	103～130GPa	銅

　実験値をもとに文献値を調べるとこのようになる。

　多少ずれてはいるが、ほぼその材質ということができる。

感想・考察

　今回の実験では最初は、鏡がずれるなどの細かいトラブルなどで時間を使ってしまった。それでも簡単に鏡は修理され、実際に実験が始まると順調に進んだ。

　今回の実験で、材料力学などでよく使う『Ｅ』がどのようにして求められたかよくわかった。計算結果の値はそれなりに近い値になったと思う。

　今回の実験では、ＳＩ単位系を用いて計算をしたがよかったのだろうか。

　たわみの式を導くところで、曲げモーメントの説明もなしに進めて後からその部分を補っておいた。今度からは順序よく導くように心がけようと思う。