
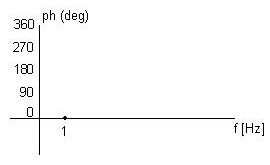
TECNO-CORNER:INTRODUZIONE ALLA TEORIA DEL SUONO (DIGITALE) Rieccoci. La scorsa volta abbiamo parlato di suoni descrivendoli come una grandezza (l'intensità del suono) che evolve nel tempo. Come vedremo,nella realtà risulta molto più utile rappresentare l'evoluzione di un suono IN FREQUENZA,piuttosto che nel tempo. La rappresentazione in FD (dominio della frequenza,abbreviato) indica come varia l'ampiezza delle varie componenti di un suono,in funzione della loro frequenza. Per esempio,ecco quale sarebbe la rappresentazione in frequenza della sinusoide vista nella prima parteLa rappresentazione in frequenza ci dà 3 tipi di informazioni: - DA QUANTE COMPONENTI è formato il segnalle audio - QUALE AMPIEZZA hanno le componenti - INTORNO A QUALI FREQUENZE si concentranoo le componenti A questo punto,è facile interpretare il grafico appena visto:descrive un segnale con una sola componente di ampiezza 1 e frequenza 1 Hz;gasp,non può che essere una sinusoide! :) Però l'informazione non è completa,perchè non conosciamo la FASE INIZIALE di questa componente. Per rispondere a questa domanda dobbiamo rappresentarne in frequenza anche la fase
Questo ci dice che la nostra componente ha fase iniziale 0 gradi:non a caso è un seno! ^^ Il primo grafico viene chiamato "diagramma del modulo in frequenza" o semplicemente "diagramma del modulo",il secondo "diagramma della fase in frequenza" o semplicemente "diagramma della fase". Insieme,hanno lo stesso potere descrittivo della rappresentazione nel dominio del tempo:cioè, DATO UN SEGNALE NEL TEMPO E' POSSIBILE RAPPRESENTARLO IN FREQUENZA,E VICEVERSA. La rappresentazione di un segnale audio in frequenza si chiama SPETTRO del segnale audio, perchè "seziona" il segnale in tutte le sue componenti. A questo punto possiamo dire esattamente cosa si intende per componente di un segnale: una sinusoide ad una certa frequenza,ampiezza e fase. Questa considerazione ha portato a formulare il "TEOREMA DI FOURIER":OGNI SEGNALE AUDIO E' IL RISULTATO DELLA SOMMA DI UN CERTO NUMERO DI SINUSOIDI,CIASCUNA AVENTE UNA PROPRIA FREQUENZA, AMPIEZZA E FASE INIZIALE. Perciò,i suoni puri possono essere visti come un caso particolare dei suoni complessi:cioè, sono suoni complessi aventi una sola componente (capito perchè sono così importanti nello studio della teoria dei segnali? ;). I segnali complessi,invece,sono spesso composti da un numero elevatissimo (dell'ordine delle decine o centinaia) di sinusoidi,per cui per ricavarne lo spettro servono algoritmi matematici particolari. Faccio notare come a parità di potere espressivo,la rappresentazione in FD sia più sintetica di quella in TD:descrivere un suono nel tempo significa darne il valore di intensità per ogni istante di tempo;per descrivere lo stesso suono in frequenza basta associare a ogni componente (supposta sinusoidale) un'ampiezza e una fase. Questo fatto è tutt'altro che irrilevante,non per nulla è alla base della compressione dei segnali audio digitali (ma anche video). Nella prossima puntata:la digitalizzazione del segnale audio Andèm innanz