Предыдущая | Содержание | Следующая |
ОБЗОР ДИАГРАММНОЙ ТЕХНИКИ ПРЕДСТАВЛЕНИЯ СТРУКТУРЫ АРГУМЕНТА
Представление структуры аргумента или цепи взаимосвязанных аргументов с помощью диаграмм является эффективным инструментом неформальной логики и критического мышления, общепринятым в северо-американских учебниках. Однако в отечественной литературе диаграммная техника (ДТ) анализа структуры аргументов практически неизвестна. Учитывая как несомненную педагогическую полезность диаграммирования, так и научный интерес к этой теме, ниже мы предлагаем краткий обзор ее современного состояния.
Диаграммирование структуры аргумента можно найти еще в начале 50-х годов в учебнике М.Бердсли. Если же обратиться к
современным источникам, то с первого взгляда трудно найти какие-либо принципиальные изменения в подходе к диаграммированию и ДТ. При более углубленном исследовании как учебной, так и научной литературы по неформальной логике и критическому мышлению можно обнаружить ряд новаций, которые, однако, нуждаются в дальнейшей систематизации и развитии.
Предлагаемый ниже материал базируется на учете современной тенденции выработать более адекватный – количественный – аппарат оценки силы аргумента.
Несколько лет назад вышла монография Д.Вэлтона, ставящая ДТ на строгую математическую основу теории направленных графов или диграфов (directed graphs). Это нововведение позволяет более точно описывать структуру аргументации, чем это можно делать при традиционном подходе. Однако традиционная ДТ в общепринятом сейчас виде способна решать значительную часть возникающих задач. Поэтому мы в дальнейшем будем анализировать именно этот вариант.
![]()
Рис.1
В более сложных случаях, когда заключение обосновывается более чем одной посылкой, диаграммы делятся на два вида: с зависимыми друг от друга посылками (такие диаграммы еще называют связанными) (рис.2а) и с независимыми посылками (такие диаграммы еще называют сходящимися) (рис.2б).

Рис. 2
Наконец, распространены еще сериальные диаграммы, в котором заключение одного аргумента оказывается посылкой следующего и т.д. (рис.3).
![]()
Рис.3
Диаграммирование не только позволяет наглядно представить структуру аргумента, но и отразить силу связи посылок и заключения. На этой основе открывается возможность рассчитать существенную количественную характеристику аргумента, а именно вероятность того, что заключение является истинным. Соответствующие обозначения и формулы для сходящихся аргументов предложены в работах Роберта Янала в конце 80-х – начале 90-х годов. Проиллюстрируем это нововведение на примере.
Предположим, что 30% яблок из сада Брауна обычно оцениваются как продукт высшего сорта. Кроме того, у вас есть детектор, с помощью которого можно определить сортность яблок. К сожалению, надежность данных этого детектора составляет только 50%. Пусть вы получили яблоки из сада Брауна (R1) и детектор зафиксировал, что это яблоки высшего класса (R2). Какова надежность заключения, что это действительно яблоки высшего сорта (C)?
Традиционная диаграмма этого аргумента с двумя независимыми посылками дополняется, по Яналу, характеристиками сил связи посылок и заключения, то есть вероятности получения истинного заключения p(C|R
M), если посылка RM истинна (рис. 4).Задача состоит в том, чтобы по известным независимым друг от друга p(
C|RM) определить вероятность истинности заключения, то есть p(C|R1,R2).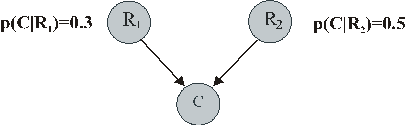
Рис.4
Алгоритм расчета p(C|R
1,R2) – “обычной суммы” – на интуитивном уровне обосновал Янал. Свое обоснование он представил в виде конкретного примера.Рассмотрим аргумент: Р1, Р2, следовательно С. Предположим, что Р1 само по себе обосновывает С с вероятностью 0,3, а Р2 ¾ с вероятностью 0,4. Очевидно, что вероятность получения С будет больше 0,4. Но какова именно ее величина? Мы можем представить обычную сумму вероятностей следующим образом. Вероятность С при заданном Р1 равна 0,3. Вычитая 0,3 из единицы, получаем 0,7. Назовем 0,7 “неизвестным”. Если теперь будет задана Р2, мы узнаем 0,4 из ранее неизвестных 0,7 или 0,4 ´ 0,7 = 0,28, то есть на 0,28 больше, чем мы знали перед этим. Поэтому мы получаем для С вероятность p(C|R1,R2) = 0,3 + 0,28 = 0,58.
Согласно этому алгоритму, для рассмотренного выше примера вероятность истинности заключения С равна p(C|R
1,R2) = 0,65!Используя введенный алгоритм, Янал предложил критерий различения аргументов с зависимыми и независимыми посылками.
Вероятность заключения аргумента с независимыми посылками равна обычной сумме отдельных вероятностей. Вероятность заключения в аргументе с зависимыми посылками не совпадает с обычной суммой отдельных вероятностей.
Этот критерий не без оснований был подвергнут критике. Однако мы не будем сейчас углубляться в полемику, а сосредоточимся на вопросе: “Является ли алгоритм Янала справедливым для аргументов с независимыми посылками?” Кроме того, будет предложено элементарное, но педагогически перспективное улучшение графического представления связей между посылками и заключением.
МОДИФИЦИРОВАННЫЙ ВАРИАНТ ДИАГРАММИРОВАНИЯ И ОЦЕНКИ АРГУМЕНТА
Прежде чем заняться проверкой алгоритма, предложенного Робертом Яналом, мы хотим ввести новые образы диаграмм, отражающих силу связи посылки и заключения. Это намерение в какой-то мере тоже предвосхищено Яналом, который предложил делить аргументы на сильные, средние и слабые в зависимости от характера посылок и силы связи посылок и заключения. Например, аргумент: “Сократ смертен (R
1), следовательно, все люди смертны (С1)” классифицируется как слабый (Weak), а аргумент “Все люди смертны (R2), следовательно, Сократ смертен (С2)” как дедуктивно валидный. В соответствующие им диаграммы включаются знаки “W” и “DV”.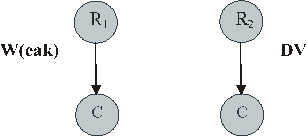
Рис.5
Однако, по нашему мнению, диаграммы могут быть сделаны графически более выразительными и информативными следующим образом (при этом предполагается, что посылки определенно истинны: условимся обозначать такого вида посылки ТМ
).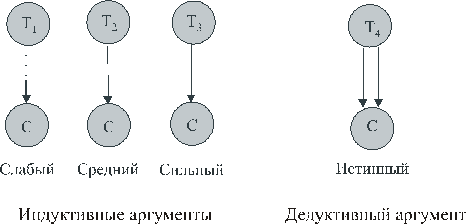
Рис.6
Для определенности разумно задать следующие количественные рамки оценок.
|
Слабый аргумент Средний аргумент Сильный аргумент Истинный дедуктивный аргумент |
0 £ p(C|…RY…) £ 1/2 1/2 < p(C|…RY….) £ 2/3 2/3 < p(C|…RY….) < 1 p(C|…TY…) = 1 |
Оценка аргумента осуществляется по двум характеристикам: по логическому значению посылок и по силе поддержки ими заключения. В случае истинных посылок сила поддержки заключения определяется “обычной суммой” вероятностей перехода от каждой из посылок к заключению – p(С|ТМ). Введенный Яналом алгоритм соответствует, очевидно, следующей формуле:
p(C|Т
1,Т2) = p(C|Т1) + [1 – p(C|Т1)] p(C|Т2). (1)Однако приведенное этим ученым обоснование нельзя признать вполне строгим и убедительным, о чем, в частности, свидетельствуют замечания Дэвида Конвея. Поэтому есть основание подвергнуть этот результат дополнительному исследованию и проверке.
На этом пути, прежде всего, обобщим (1) для произвольного числа посылок 1 £ М £
¥ .p(C|T1,T2) = p(C|T1) + {1 – p(C|T1)} p(C|T2)
p(C|T1,T2,T3) =
= p(C|T1) + [1 – p(C|T1)] p(C|T2) +
+{1 – p(C|T1) – [1-p(C|T1)] p(C|T2)} p(C|T3)= (2)
= p(C|T1,T2) + {1- p(C|T1,T2)} p(C|T3)
……………………………………………………
p(C|T1… TM) = p(C|T1… TM-1) +{1 – p(C|T1… TM-1)} p(C|TM).
Ниже сформулируем ряд необходимых условий, которым должна отвечать функция (1) или любое ее обобщение.
Первое из этих условий C1 выражает тот факт, что правильно рассчитанная вероятность всегда принимает значения от 0 до 1. Условие С2 состоит в том, что значение вероятности получения истинного заключения не зависит от процедуры подсчета, то есть от порядка учета составляющих p(C|R
M). Третье условие фиксирует тот факт, что если заключение С получает достаточное основание хотя бы в одной посылке p(C|RX) = 1, то прибавление остальных не изменяет вероятности заключения и p(C|R1…. RX, RX+1 … RM) = 1. Условие С4 фиксирует тот факт, что если какая-то посылка не поддерживает заключения p(C|RX) = 0, то ее учет или неучет никак не влияет на конечный результат p(C|R1… RM). При истинных посылках эти условия принимают следующий вид:|
0£ p(C|Т1… ТM) £ 1,p(C|…Т X, ТX+1 …) == p(C|…Т X+1,ТX …) etc.,если p(C|Т X) = 1, 1£ X £ M,то p(C|…Т X…) = 1,если p(C|Т X) = 0, 1 < X < M,то p(C|…Т X-1, ТX, ТX+1…) == p(C|…Т X-1, ТX+1 …). |
С1¢ С2¢ С3¢ С4¢ |
Проверим теперь выполнение условий С1¢ – С4¢ для формулы (1).
При правильной постановке задачи 1 ³
p(C|T1) ³ 0 и 1 ³ p(C|T2) ³ 0, поэтому p(C|T1,T2) ³ 0. С другой стороны, 1 – p(C|T1) ³ (1 – p(C|T1)) p(C|T2), поэтому 1 ³ p(C|T1) + (1 – p(C|T1)) p(C|T2). Следовательно, С1¢ выполняется.С2¢ выполняется в силу симметричного вхождения в него p(C|T
1) и p(C|T2).С3¢ выполняется постольку, поскольку при p(C|T
1) = 1 множитель при p(C|T2) обращается в 0, что сводит к нулю вклад этой составляющей. Аналогичный вывод для p(C|T2) = 1 следует из учета С2¢ .С4¢ для (1) при p(C|T
1) = 0 выполняется очевидным образом; в силу С2¢ оно выполняется и при p(C|T2) = 0.Нетрудно доказать выполнимость С1¢ – С4¢ и для обобщения (2), но эти упражнения оставим для наиболее любознательных. Сейчас же просто проверим справедливость (2) на одном конкретном примере.
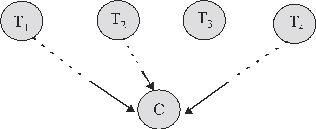
Рис.7
Шаг за шагом из (2) для p(C|T
1,T2,T3,T4) получаем:p(C|T1,T2) = 0,1 + (1 – 0,1) ´ 0,5 = 0,55;
p(C|T1,,T2,T3) = 0,55 + (1 – 0,55) ´ 0 = 0,55;
p(C|T1,T2,T3,T4)=0,55+(1- 0,55) ´ 0,01= 0,5545.
Повторим упражнение, например, для p(C|Т
2,Т4,Т1,Т3):p (C|T2,T4) = 0,5 + (1 – 0,5) ´ 0,01 = 0,505;
p (C|T2,T4,R1) =0,505+(1-0,505) ´ 0,1 = 0,505+0,0495 = 0,5545;
p(C|T2,T4,T1,T3) = 0,5545 + (1 – 0,5545) ´ 0 = 0,5545.
Следовательно, p(C|T
1,T2,T3,T4) = p(C|T2,T4,T1,T3) в полном соответствии с С1¢ , С2¢ , С4¢ , что и требовалось доказать!Но полученные формулы (1) и (2) предполагают дальнейшее обобщение, а именно на случай, когда логическое значение исходных посылок точно не известно, а задана лишь вероятность того, что посылка HМ истинна – P(H
M). Задание такой вероятности графически фиксируется стрелкой над посылкой. Назовем такого рода посылки и построенные на них аргументы гипотетическими. Соответствующие им простейшие диаграммы будут иметь вид (рис.8a, 8б).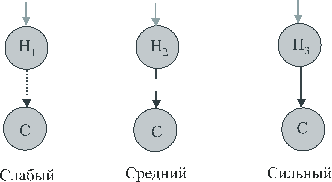
Гипотетические индуктивные аргументы
Рис.8а
![]()
Гипотетический дедуктивный аргумент
Рис.8б
Понятно, что в случае гипотетических аргументов нельзя отождествлять силу связи посылок и заключения и силу поддержки посылкой заключения. Поэтому сила, например, дедуктивного аргумента зависит как от связи между посылками H
M и заключением – p(C|HM), так и от вероятности P(HM).Согласно теории вероятности для условной вероятности имеем p(C|H
M) = P(C&HМ)/P(HM), следовательно P(C&HМ) = P(HM)p(C|HM). Например, если P(H1) = 0,7 и p(C|H1) = 0,7, то вероятность одновременной истинности посылки и заключения будет 0,49 (аргумент средней силы). Пусть p(C|H2) = 1, но P(H2) = 0,1. Тогда p(C&H2) = 0.1 и получаем слабый дедуктивный аргумент!На основании предпринятого обобщения нетрудно перейти к расчету сериальных диаграмм, включающих гипотетические посылки. Например, если p(H
1|Т1) = 0,7, p(C|H1) = 0,7, то получим уже упомянутый выше результат P(Т1&H1&C) = p(H1|Т1) p(C|H1) = 0,49.![]()
Рис.9
Нетрудно обобщить сказанное для диаграммы аргумента с двумя независимыми гипотетическими посылками.
P(C&H1&H2)=P(H1)p(C|H1)+[1–P(H1)p(C|H1)]P(H2) p(C|H2) (3)
Проверим выполнение условий С1, С2 для формулы (3) на конкретном примере, которому соответствует рис. 10.

Рис. 10
Вероятность истинности суждения о неисправности тормозов автомобиля, недавно прошедшего техосмотр, составляет Р(H1) = 0,0001. Вероятность истинности суждения о неисправности двигателя Р(H2) = 0,01. Вероятность быстрой аварии для автомобиля с неисправными тормозами составляет p(C|H1) = 0,9, а с неисправным двигателем p(C|H2) = 0,25. Какова вероятность правильности прогноза о том, что этот автомобиль вскоре попадет в аварию?
P(C&H1&H2) = P(H1) p(C|H1) + [1 – P(H1) p(C|H1)] P(H2) p(C|H2) = 0,0001 ´ 0,9 + (1 – 0,00009) ´ 0,01 ´ 0,25 =0,002589775,
P(C&H2&H1) = 0,01 ´ 0,25 + (1 – 0,0025) ´ 0,0001 ´ 0,9 = 0,002589775.
Рассмотрим случай, когда вероятность отказа двигателя исключена, то есть
P(H2) = 0, и рассчитывается вероятность аварии только вследствие отказа тормозов.P(C&H1&H2) = 0,0001 ´ 0,9 + (1 – 0,00009) ´ 0 ´ 0,25 = 0,00009
Проверка выполнимости условия С3, также, как и дальнейшее обобщение для диаграмм с большим числом посылок и последовательных шагов не представляет труда. Она легко поддается аналитическому описанию и удобна для расчета на компьютере. Однако в силу ее тривиальности и громоздкости здесь этого мы делать не будем.
Теперь рассмотрим случай, когда вероятность истинности посылки равна нулю. Смысл этого достаточно ясен – посылка FМ ложна, она не соответствует действительности.
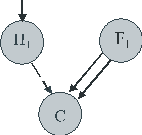
Рис. 11
Важно понять, что из ложной посылки может быть выведено, например, дедуктивно валидное заключение, однако оно не будет иметь никакой поддержки со стороны FМ! Рассмотрим в качестве примера следующую диаграмму: P(H
1)=0,5, p(C|H1) = 0,6, P(F1) = 0, p(C|F1) = 1.P(C&H1&F1) = P(H1)p(C|H1)+[1-P(H1)p(C|H1)]P(F1)p(C|F1) =
= P(H1) p(C|H1) = 0,3.
Еще раз обратим внимание на то, что в случае ложных или гипотетических посылок сила связи посылки и заключения не тождественна силе поддержки заключения данной посылкой, что имеет место только в случае истинных посылок!
В заключение представим примеры диаграмм еще одного класса аргументов – плохих аргументов (рис 12).
Кроме всех дедуктивных и индуктивных аргументов с ложными посылками, к плохим аргументам относятся аргументы с посылками не ложными (истинными или гипотетическими), но никак не относящимися к рассматриваемому заключению: такие посылки называют иррелевантными.
Точности ради нужно отметить, что если мы имеем сложный аргумент с независимыми посылками, среди которых есть как ложные, так и истинные, то он не будет a priori плохим: его сила определяется поддержкой заключения только истинными посылками.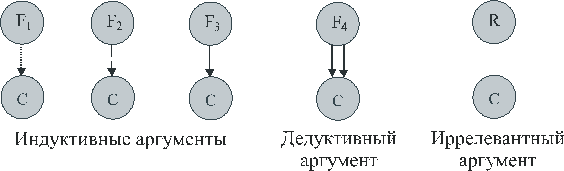
Рис.12
В показаниях свидетелей А, В и Х содержатся независимые доказательства, принятие которых с необходимостью приводит к выводу, что ограбление банка было совершено известным “медвежатником” Y. Но в ходе расследования было установлено, что показания А и В могут быть истинны, соответственно, с вероятностями Р(H1) = 0.3 и Р(H2) = 0.5, тогда как Х явно клеветал на подозреваемого и поэтому Р(F3) = 0. Какова вероятность того, что ограбление совершил Y?

Рис. 13
P(C&H1&H2) = P(H1) p(C|H1)+[1-P(H1) p(C|H1)] P(H2) p(C|H2) = P(H1) + [1 – P(H1)] P(H2) = 0,65,
P(C&H1&H2& F3)=P(C&H1&H2)+[1–P(C&H1&H2)]P(F3)= 0,65.
Следовательно, в вероятность истинности утверждения виновности Y в совершении преступления вклад вносят только показания двух первых свидетелей, тогда как лжесвидетельство Х при решении этого вопроса не принимается во внимание.
Описанные нововведения, по нашему мнению, не исчерпывают возможностей улучшения традиционного способа диаграммирования аргументов. Имеет смысл графически отображать и при их оценке учитывать не только основания pro, но и contra и т.д. Эти возможности требуют дополнительного изучения как в плане научного обоснования их содержания, так и в плане нахождения оптимальной педагогически формы.
Результатом дальнейшего развития диаграммной техники анализа и оценки аргумента будет совершенствование инструмента решения соответствующих интеллектуальных задач и принятия решений.
Предыдущая | Содержание | Следующая |