La Sezione Aurea e i Numeri di Fibonacci


Umberto Cerruti - Università di Torino



1 - La Sezione Aurea

Nel capitolo VII del Timeo, Platone riferisce queste parole di Socrate:

Fra i legami il più bello è quello che faccia, per quanto è possibile, un'unica cosa di sé e dei termini legati insieme; ed è la proporzione che realizza ciò nel modo migliore. Perché quando di tre numeri, o masse, o potenze che siano, il medio sta all'ultimo come il primo sta al medio, e d'altra parte il medio sta al primo come l'ultimo sta al medio, allora il medio, divenendo primo e ultimo, e l'ultimo e il primo divenendo medi, così accadrà che tutti diventino necessariamente la stessa cosa, e diventando la stessa cosa fra loro, saranno tutti un'unità.

Il "legame" di cui qui si parla è evidentemente la proporzione geometrica:

P : Q = Q : R

Il rapporto tra P e Q è uguale a quello tra Q e R.
Q è detto termine medio della proporzione, o medio proporzionale.

Si noti che

Q2 = P·R
Pertanto un rettangolo di lati P ed R è equivalente (cioé ha la stessa area) ad un quadrato di lato Q.

Nella proposizione 11 del libro II degli Elementi, Euclide si chiedeva:

Come dividere un segmento in modo che il rettangolo che ha per lati
l' intero segmento e la parte minore sia equivalente al quadrato che ha per lato la parte maggiore.

Per quanto detto il problema è equivalente a questo:

Dividere un segmento dato in due parti tali che la parte maggiore sia media proporzionale tra la parte minore e l'intero segmento.

Una soluzione classica è la seguente:

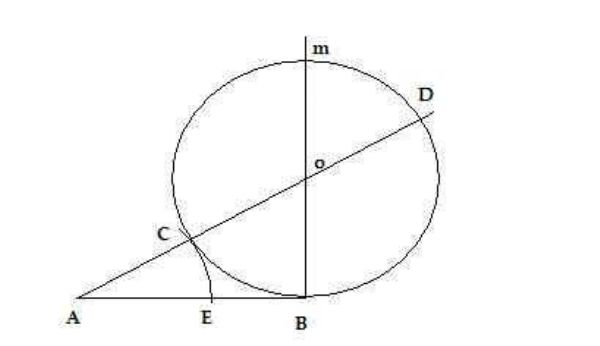
Euclide, libro II
Figura 1

Dato il segmento AB costruiamo un cerchio di uguale diametro e ad esso tangente in B. Tracciamo la secante AD. E' noto che la tangente AB è il termine medio della proporzione tra AD e AC. Ovvero:

(1) AD : AB = AB : AC

Dalla (1) e dalla costruzione di Figura 1 si ricava: 

(AD-AB) : AB = (AB-AC) : AC
AC : AB = EB : AC
AE : AB = EB : AE
e infine:

(2) EB : AE = AE : AB

La (2) prova che effettivamente la costruzione di Figura 1 permette di dividere un qualsiasi segmento AB in due parti AE e EB tali che il rettangolo di lati AB, EB è equivalente al quadrato di lato AE.

Il rapporto AE:EB (o, ciò che è lo stesso, il rapporto AB:AE) viene detto sezione aurea. Si noti che questo rapporto è indipendente dalla lunghezza AB del segmento di partenza.

2 - Il Rettangolo Aureo

Un rettangolo tale che il rapporto tra il lato maggiore e quello minore sia la sezione aurea viene detto rettangolo aureo.

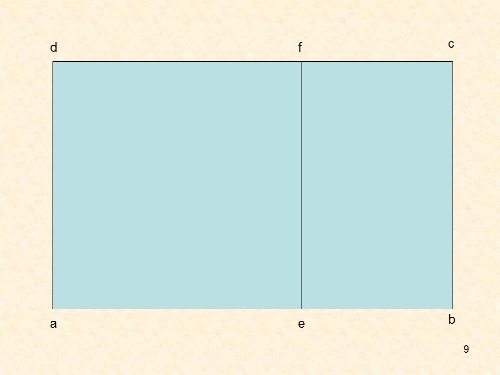
Rettangolo Aureo
Figura 2

Nella Figura si vede un rettamgolo di lati ab e bc, dove bc è uguale a ae e, come nella Figura 1, si ha:

ab:ae = ae:eb = sezione aurea
Poiché bc è uguale a ae il rapporto tra il lato maggiore e quello minore è la sezione aurea e pertanto il rettangolo abcd è un rettanglo aureo. Levando da abcd il quadrato di lato ae rimane il rattangolo ebcf. Poiché
bc:eb = ae:eb = sezione aurea
anche ebcf è un rettangolo aureo. Possiamo concludere che:

Se da un rettangolo aureo si sottrae il quadrato costruito sul lato minore, rimane un rettangolo aureo.

Chiaramente questa costruzione si può ripetere quante volte si vuole.

Nove Rettangoli Aurei
Figura 3

Si determina così una sequenza infinita di rettangoli aurei, dove ognuno si ottiene dal precedente levando il massimo quadrato in esso contenuto.

Guardando attentamente, in Figura 3 si osservano nove rettangoli aurei.
In questa direzione si precipita vertiginosamente verso l'infinitamente piccolo. Ma si può anche seguire il cammino opposto:

Se, dato un rettangolo aureo, si costruisce un quadrato sul suo lato maggiore, il rettangolo risultante è aureo.

Cinque Rettangoli Aurei
Figura 4

Nella Figura 4 si parte dal rettangolo aureo iniziale R e si aggiungono in sequenza quattro quadrati, ottenendo quattro nuovi rettangoli aurei R1, R2, R3 e R4, dove:

R1 = R + q1
R2 = R1 + q2
R3 = R2 + q3
R4 = R 3+ q4

Osserviamo che, in entrambe le costruzioni, i rettangoli che si ottengono hanno la stessa forma (infatti la forma di un rettangolo è determinata completamente dal rapporto dei lati), Essi crescono o rimpiccioliscono mantenendo inalterata la forma.
Le medesime costruzioni si possono applicare a partire da un qualunque rettangolo nel piano, ma - se esso non è aureo - daranno luogo a rettangoli di forme diverse.

Se si parte da un rettangolo R nel piano si noterà che, ad ogni passo, sia verso l'interno che verso l'esterno, ci sono due possibilità di sviluppo della figura, perché il quadrato si può togliere (o aggiungere) da un lato o dall'altro. Ad ogni passo il rettangolo ruota di 90 gradi. Se si fissa un verso di rotazione e si toglie (o si aggiuge) il quadrato sempre dalla stessa parte (ruotando come osservatori solidali con esso) si ottiene una figura frattale. Supponiamo di procedere all'infinito, di riempire R con la costruzione verso l'interno e la parte rimanente del piano con quella verso l'esterno. Se ora ci solleviamo e guardiamo la tassellazione ottenuta (il disegno delle piastrelle) essa apparirà uguale a quasiasi distanza! Se ci avviciniamo al centro, dove i rettangoli diventano piccolissimi, e facciamo uno zoom (guardiamo con una lente di ingrandimento) vediamo sempre la stessa figura!

3 - Il numero d'oro

Fino ad ora abbiamo trattato della sezione aurea come di un rapporto tra lunghezze, il cosiddetto rapporto aureo. A questo rapporto corrisponde un numero, (il numero d'oro) che ora calcoleremo.

Ricordiamo la

(2) EB : AE = AE : AB

Poniamo

x = AE
y = EB
Poiché AB è la lunghezza del segmento intero si ha:
AB = x + y
e dalla (2) si ottiene l'equazione:

(3) x2 = y (x + y)
Dividendo entrambi i lati per y2 e riordinando si ha:
(4) (x/y)2 - x/y -1 = 0
Si noti che x/y è il valore di AE:EB, cioé il valore numerico della sezione aurea. La (4) ha due soluzioni, che sono:
x/y = (1 + Ö5)/2
x/y = (1 - Ö5)/2
Soltanto la prima è accettabile, in quanto la seconda è negativa.

Solitamente la sezione aurea viene denotata con la lettera greca Φ (phi maiuscolo)

Abbiamo allora dimostrato che:

(5) Φ = (1 + Ö5)/2


Approssimativamente (con 50 decimali dopo la virgola) Φ vale:

(6) Φ = 1.61803398874989484820458683436563811772030917980576...


Dalla (4) si ottiene subito la relazione fondamentale:

(7) Φ2 = 1 + Φ


Moltiplicando entrambi i lati della (7) per Φn - 2 si ottiene la relazione di ricorrenza per Φ:

(7') Φn = Φn-2 + Φn-1


E' facile ora calcolare il reciproco di Φ.
Dividendo entrambi i lati della (3) per x2 e riordinando si ha:

(8) (y/x)2 + y/x -1 = 0
Anche la (8) ha due soluzioni, che sono:
y/x = (-1 + Ö5)/2
y/x = (-1 - Ö5)/2
Ancora una volta soltanto la prima è accettabile, perché la seconda è negativa.

Di solito il reciproco della sezione aurea viene denotato con la lettera greca φ (phi minuscolo).

Pertanto:

(9) φ = (-1 + Ö5)/2


La parte decimale di φ è identica a quella di Φ perché:

(10) Φ = 1 + φ


Ne segue che φ vale:

(11) φ = 0.61803398874989484820458683436563811772030917980576...


Dalla (8) si ottiene subito la relazione fondamentale:

(12) φ2 = 1 - φ


Moltiplicando entrambi i lati della (12) per φn - 2 si ottiene la relazione di ricorrenza per φ:

(12') φn = φn-2 - φn-1


Ci sono altre relazioni utili. Dalla definizione stessa di φ abbiamo:

(13) Φ = 1/φ


La (13) con la (10) dà:

(14) Φ = 1 + 1/Φ


Giocando con i rettangoli aurei, come nel paragrafo 2, mi sono posto alcuni problemi. Uno di essi è il seguente:

C'è una relazione semplice tra le lunghezze dei lati del rettangolo iniziale e quelle dell'n-esimo rettangolo costuito?

Consideriamo la fuga verso l'interno. Supponiamo che il lato minore del rettangolo iniziale (rettangolo 0) sia lungo 1 (questo significa semplicemente che si misurerà tutto usando la lunghezza del lato minore come unità di misura). Allora, per definizione di rettangolo aureo, il lato maggiore sarà lungo Φ.
Il secondo rettangolo (rettangolo 1) ha lato maggiore uguale al lato minore del primo, quindi affinché si mantenga il rapporto aureo, i suoi lati avranno lunghezze:

lato maggiore = 1
lato minore = 1/Φ
Il terzo rettangolo (rettangolo numero 2 della costruzione) ha lato maggiore uguale al minore del precedente. Quindi affinché si mantenga il rapporto aureo, i suoi lati avranno lunghezze:
lato maggiore = 1/Φ
lato minore = 1/Φ2
E' ora immediato provare, per induzione, che
(15) I lati del rettangolo n-esimo (nella costruzione verso l'interno) hanno lunghezze:
lato maggiore = 1/Φn-1
lato minore = 1/Φn
Dalla (13) si ottiene subito la
(15') I lati del rettangolo n-esimo (nella costruzione verso l'interno) hanno lunghezze:
lato maggiore = φn-1
lato minore = φn
E' un risultato interessante. Consideriamo la successione dei rettangoli Ro (quello iniziale), R1, R2, ..., Rn,... Da quanto visto le lunghezze dei lati minori di questi rettangoli formano la successione:
φ0 = 1, φ, φ2, ...., φn, ...
Si tratta di una progressione geometrica di ragione φ.

Sommando i termini della successione si ha la serie geometrica:

Serie Aurea: 1 + φ + φ2 + .... + φn + ...
E' ben noto che la somma di una serie geometrica di ragione r minore di 1 è finita e vale:
(16) 1/(1 - r)
Dunque, utilizzando la (12) si ha:
(17) La somma della Serie Aurea vale 1/φ2
Equivalentemente:
(17') La somma della Serie Aurea vale Φ2
O ancora, dalla (7):
(17'') La somma della Serie Aurea vale 1 + Φ
Da questa si ricava immediatamente:
(18) Φ = φ + φ2 + .... + φn + ...
Possiamo arrivare da soli a questi risultati, anche senza conoscere la (16), partendo dal solo fatto che la somma della nostra serie esiste ed è finita: 
Denotiamo con α la somma della Serie Aurea,
α = 1 + φ + φ2 + .... + φn + ...
raccogliendo φ si ha:
α = 1 + φ (1 + φ + φ2 + .... + φn + ...)
ovvero
α = 1 + φ α
e infine
α = 1/(1 - φ)
La somma dei primi 10 termini della Serie Aurea dà
2.604878371253470009248...
e solo il primo decimale è corretto. La somma dei primi 100 termini dà
2.618033988749894848202...
con 20 cifre corrette dopo la virgola.

Con la Serie Aurea ci si può divertire, si possono ottenere senza fatica risultati sorprendenti. Facciamo un esempio:

1 + Φ = 1 + φ + φ2 + .... + φn + ... =
1 + (φ + φ2) + (φ3 + φ4) + ... =
1 + (1 + φ) φ + (1 + φ) φ3 + ... = 
1 + (1 + φ) (φ + φ3 + φ5 + ...) =
1 + Φ (Somma delle potenze dispari di φ)
Pertanto la somma delle potenze dispari di φ vale 1.
Conseguentemente:
La somma delle potenze pari di φ vale Φ.
Esaminiamo ora la costruzione dei rettangoli aurei verso l'esterno. Partiamo dallo stesso R0 di prima, di lati 1 e Φ. Poniamo S0 uguale a R0e denotiamo con S1, S2, S3... la sequenza dei rettangoli via via generati.

La regola è la seguente:

Sn+1 si ottiene da Sn costruendo un quadrato
sul lato maggiore di Sn
Ne segue immediatamente che:

  • Il lato minore di Sn+1 è uguale a quello maggiore di Sn
  • Il lato maggiore di Sn+1 è la somma dei due lati di Sn

    Il rettangolo S0 ha lati (minore e maggiore), come si è detto, 1 e Φ. 
S1 ha lati Φ e (1 + Φ) = Φ2.
S2 ha lati Φ2 e (Φ + Φ2) = Φ3.
etc.
In questo calcolo abbiamo usato la relazione di ricorrenza (7').
    Concludendo, abbiamo dimostrato che
    (19) I lati del rettangolo n-esimo (nella costruzione verso l'esterno) hanno lunghezze:
    lato maggiore = Φn+1
    lato minore = Φn
    Naturalmente per ottenere questo risultato sarebbe stato sufficiente usare la regola di costruzione e il fatto che il rapporto tra i lati rimane sempre Φ. E' però molto interessante, e utile, avere una dimostrazione diversa che usa la ricorrenza.

    4 - L'apparizione dei Fibonacci

    Supponiamo di fissare un segmento AB come unità di misura. Siamo allora in grado di costruire, con riga e compasso, segmenti di lunghezza φ e Φ. Per esempio la costruzione della Figura 1 ci fa subito trovare φ, che è AE. Possiamo immediatamente costruire Φ prolungando AB (che vale 1) di un segmento uguale a AE. Per la (10) il segmento risultante ha lunghezza Φ.

    E' possibile - dato un intero n positivo - costruire, con riga e compasso, i rettangoli Rn e Sn?

    Visti i risultati (15') e (19) la domanda è equivalente a:

    E' possibile - dato un intero n positivo - costruire, con riga e compasso, segmenti di lunghezza Φn e φn?

    Tentiamo di scrivere ogni Φn nella forma a + b Φ, con a e b interi.

    Se n è 0, Φ0 è 1. Dunque a, b valgono, rispettivamente, 1 e 0.
    Se n è 1, Φ1 è Φ. Dunque a, b valgono, rispettivamente, 0 e 1.
    Se n è 2, Φ2 è 1 + Φ, per la (7). Pertanto a e b valgono 1 entrambi.
    Se n è 3, Φ3 è Φ + Φ2 per la (7'). Dunque, per il risulato precedente, Φ3 vale 1 + 2 Φ. In questo caso a e b sono, rispettivamente, 1 e 2.
    E' chiaro come si può proseguire. Nella tavola sottostante si riportano i valori di a e b per n che va da 0 a 10:

    
(20)


n	a	b
0	1	0
1	0	1
2	1	1
3	1	2
4	2	3
5	3	5
6	5	8
7	8	13
8	13	21
9	21	34
10	34	55
    Chi ha visto almeno una volta la successione dei numeri di Fibonacci, la riconoscerà immediatamente nelle due colonne sottostanti ad a e b.

    Leonardo Pisano, detto Fibonacci, fu un grande matematico e visse tra il 1170 e il 1250. Nel 1202 scrisse il Liber Abaci, uno dei capolavori della letteratura matematica. Nel terzo capitolo di questo libro Fibonacci poneva un problema riguardante una popolazione ideale di conigli:

    Ipotesi:
  • Una coppia di conigli matura produce ogni mese una coppia immatura.
  • Dopo un mese dalla nascita una coppia immatura diventa matura.
  • Nessun coniglio muore.
  • All'inizio c'è una coppia immatura.
    Domanda:
  • Quante coppie ci sono dopo un anno?
    • Diciamo Fn il numero delle coppie di conigli al mese n, e calcoliamo:
    
A gennaio c'è una coppia immatura A: F1 = 1
A febbraio c'è una coppia matura A: F2 = 1
A marzo A produce una coppia immatura B: F3 = 2
Ad aprile A produce una coppia immatura C, e B matura: F4 = 3
A maggio ci sono certamente A, B e C. C matura.
A e B producono due coppie immature: F5 = 5
Etc. etc.
    La legge è ora evidente:
    (21) Fn = Fn-1 + Fn-2
    La legge è formalmente identica alla (7'), ed è esattamente questo il motivo per cui i numeri di Fibonacci appaiono nella tavola (20).

    Abbiamo pertanto trovato i numeri interi (a e b) che cercavamo. Ora sappiamo che:

    (22) Φn = Fn-1 + Fn Φ

    Quindi i rettangoli aurei esterni si possono effettivamente costruire con riga e compasso, a partire da un segmento U di lunghezza 1 e da un segmento V di lunghezza Φ. Per esempio per disegnare S9 dobbiamo tracciare i due lati, che hanno lunghezze Φ9 e Φ10. Dalla 22 Φ9 si ottiene riportando di seguito su una retta 21 copie di U e 34 copie di V. Per il lato maggiore occorrono 34 copie di U e 55 copie di V.

    Passiamo alla sequenza dei rettangoli interni, cioé alla costruzione con riga e compasso delle quantità φn. Seguiamo la stessa tattica che abbiamo usato prima.

    Tentiamo di scrivere ogni φn nella forma c + d φ, con c e d interi.

    Se n è 0, φ0 è 1. Dunque c, d valgono, rispettivamente, 1 e 0.
    Se n è 1, φ1 è φ. Dunque c, d valgono, rispettivamente, 0 e 1.
    Se n è 2, φ2 è 1 - φ, per la (12). Pertanto c è 1 mentre d è -1.
    Se n è 3, Φ3 è φ - φ2 per la (12'). Dunque, per il risulato precedente, φ3 vale -1 + 2 φ. In questo caso c e d sono, rispettivamente, -1 e 2.
    La (23) è l'analogo della tavola (20):

    
(23)


n	c	d
0	1	0
1	0	1
2	1	-1
3	-1	2
4	2	-3
5	-3	5
6	5	-8
7	-8	13
8	13	-21
9	-21	34
10	34	-55
    E' facile ora concludere che:
    (24) φn = (-1)n (Fn-1 - Fn φ)

    Per disegnare R9 dobbiamo disporre delle lunghezze φ8 (il lato maggiore) e φ9 (il lato minore). Supponiamo di avere i segmenti U e W di rispettive lunghezze 1 e φ. Otteniamo φ8 in questo modo: partiamo da un punto su una retta e riportiamo 13 volte U procedendo verso destra, quindi invertiamo la direzione e riportiamo 21 volte φ. Si procede allo stesso modo per φ9.

    E' istruttivo vedere insieme la (22) e la (24):

    (22) Φn = Fn-1 + Fn Φ
    (24) φn = (-1)n (Fn-1 - Fn φ)

    Poiché

    (-φ)n = (-1)n φn

    moltiplicando entrambi i lati della (24) per (-1)n otteniamo:

    (22) Φn = Fn-1 + Fn Φ
    (24') (-φ)n = Fn-1 - Fn φ
    Sottraendo la (24') dalla (22) si hanno le:
    (25) Φn - (-φ)n = Fn (Φ + φ)

    cioé:


    (25')

    Ricordiamo ora la (5) e la (9);

    (5) Φ = (1 + Ö5)/2
    (9) φ = (-1 + Ö5)/2
    Da queste e dalla (25') si ottiene per Fn la seguente espressione:


    (26)

    La (26) è veramente un risultato straordinario! Ricordiamo che i numeri di Fibonacci sono definiti da una relazione ricorsiva: si ottiene l'elemento n-esimo sommando i due precedenti. Apparentemente quindi per calcolare F100 è necessario conoscere F99 e F98. Invece la (26) dà F100, o Fn, in un colpo solo, senza richiedere la conoscenza degli elementi precedenti.

    Inoltre la formula (26) contiene potenze di numeri irrazionali, mentre Fn è un numero intero!

    5 - Il più nobile di tuti i numeri!

    Il questo paragrafo parleremo di uno strumento matematico poco noto ma estremamente utile e potente: le frazioni continue.

    L'espressione in frazione continua (abbreviato FC) di un numero α è la seguente:

    Frazione continua
    (27)

    I coefficienti che appaiono nella (27) sono chiamati quozienti parziali.

    Se α è irrazionale la FC che lo esprime è infinita. Questo è il caso che ci interessa. Se la FC si taglia ad un certo punto si ottiene una frazione, un numero razionale, che viene detto convergente di α.

    Diciamo Pk/Qk il k-esimo convergente.

    Con semplici calcoli troviamo:

    P0/Q0 = a0 = a0/1
    P1/Q1 = a0 + 1/a1 = (1 + a0a1)/a1
    P2/Q2 = a0 + 1/(a1 + 1/a2)) = (a0 + a2 + a0a1a2) /(1 + a1a2)

    I convergenti si possono calcolare ricorsivamente:

    (28)
    Dati:
    P0 = a0, Q0 = 1
    P1 = 1 + a0a1, Q1 = a1
     Per ogni k > 1 si ha:
    Pk = akPk-1 + Pk-2
    Qk = akQk-1 + Qk-2

    Vediamo ora come si determinano i quozienti parziali ak. Ricordiamo che con [z] si intende la parte intera di z, ovvero il più grande intero minore o uguale a z.

    (29) - Procedimento per la generazione dei quozienti parziali di α
    Poniamo α0 = α e a0 = [α0].
    Per ogni k > 1 definiamo αk e ak così:
    αk = 1/(αk-1 - ak-1)
    ak = [αk]

    E' facile calcolare lo sviluppo in FC di una irrazionalità quadratica Ön. Proviamo con Ö3:

    (30) Sviluppo in frazione continua di Ö3
    α0 = Ö3, a0 = [Ö3] = 1.
    α1 = 1/(α0 - a0) = 1/(Ö3 - 1)
    e, moltiplicando sopra e sotto per Ö3 + 1:
    α1 = (Ö3 + 1)/2.
    a1 = [α1] = 1.
    α2 = 1/(α1 - a1) = 1/((Ö3 + 1)/2 - 1) = 2/(Ö3 - 1)
    e, moltiplicando sopra e sotto per Ö3 + 1:
    α2 = Ö3 + 1.
    a2 = [α2] = 2.
    α3 = 1/(α2 - a2) = 1/((Ö3 + 1) - 2) = 1/(Ö3 - 1) = α1:
    da questo punto in poi gli ak si ripetono, pertanto:
    Ö3 = [1, 1, 2, 1, 2, 1, 2, ... ].
    Sussiste il notevole teorema (che in parte era già noto a Euclide):
    (31)
    Un numero α ha FC periodica se e solo se α = (a + Ön)/b
    dove a, b sono interi qualsiasi (ovviamente b ¹ 0) ed n è un intero positivo non quadrato.
    Inoltre:
    (32)
    Se α = Ön, con n positivo non quadrato allora:
    1) Il periodo comincia subito dopo a0.
    2) L'ultimo termine amdel periodo è sempre uguale a 2a0.
    3) La parte di periodo a1, a2, ..., am-1 è una palindrome.
    Ovvero:
    Ön = [a0, a1, a2, a3, ...., am-1, 2a0, a1, a2, a3, ..., am-1,2a0, ... ]
    dove [a1, a2, a3, ..., am-1] = [am-1, am-2, am-3, ..., a1]
    Come esempio di quanto asserito nella (32) esaminiamo la FC di Ö2005:
    Ö2005 = [44, 1, 3, 2, 21, 1, 16, 1, 21, 2, 3, 1, 88, 1, 3, 2, ... ]
    Il periodo termina con 88 e [1, 3, 2, 21, 1, 16, 1, 21, 2, 3, 1] è una palindrome.

    La FC di α serve a creare una successione di approssimazioni sempre migliori di α. Queste approssimazioni sono i convergenti Pk/Qk.
    Per semplificare le notazioni poniamo

    Ck = Pk/Qk
    Si dimostra che:
    (33)
    1) La successione dei convergenti Ck ha come limite α
    2) Per ogni k C2k < α < C2k+1
    3) |α - Ck| < 1/(QkQk+1)

    La (33.1) non è particolarmente interessante, a prima vista. Ci sono infinite sequenze di numeri razionali che convergono ad α. La più ovvia, è più usata, è quella data dalla espressione decimale infinita di α. Prendiamo come esempio un personaggio unico, potente e famoso: π.

    π = 3,1415926535897932384626433832795028841971...
    La sequenza dei razionali:
    (34)
    3/1, 31/10, 314/100, 3141/1000, 31415/10000, ....
    coverge a π.

    Se sviluppiamo π in FC troviamo:

    (35)
    π = [3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1 ...]
    e la sequenza dei convergenti è (da C0 a C12):
    3, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532, 833719/265381, 1146408/364913, 4272943/1360120, 5419351/1725033, 80143857/25510582, ...
    I razionali della (34) approssimano tutti π per difetto, mentre la (33.2) dice che i convergenti della (35) "colpiscono" una volta a sinistra e una volta a destra del bersaglio. Tutti i pari sono a sinistra e tutti i dispari a destra. Ma la cosa più importante è la precisione dei "colpi"!

    Dalle (28) e (33.3) si ricava che un convergente Ck è una approssimazione particolarmente efficace quando ak+1 fa un salto di grandezza rispetto ai precedenti quozienti parziali. Nel tratto iniziale di π questo avviene per k uguale a 1 e a 3.

    (36)
    Nelle (35) leggiamo che
    C1 = 22/7
    ora 22/7 = 3,142... approssima π con due decimali esatti e
    C3 = 355/113 = 3.1415929... approssima π con sei decimali esatti!
    Quanto detto nella (36) non è un caso, infatti vale questo formidabile risultato:
    (37)
    I convergenti Ck = Pk/Qk di α sono le migliori approssimazioni possibili ad α.
    Lo sono in questo senso molto preciso:
    Tra tutte le frazioni i cui denominatori sono minori di una data quantità, quella che è più vicino ad α è sempre uno dei convergenti di α.
    Questo è il motivo per cui certe frazioni, come 22/7 (Archimede, 287-212 AC) e 355/113 (Zu Chongzhi, 429-500) sono note fin dall'antichità.

    Veniamo ora alla nostra amata sezione aurea Φ. Determiniamo la sua FC con il procedimento (29)

    (38)
    Φ0 = Φ, a0 = [Φ] =1.
    Φ1 = 1/(Φ -1) = Φ per la relazione fondamentale (7).
    Dunque a1 = [Φ1] = 1. Da questo punto tutto si ripete e infine:
    Φ = [1, 1, 1, 1, 1, .... ]
    Calcolando i convergenti a Φ con le (28) otteniamo la sequenza:
    1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, 233/144, 377/233 ...
    Ovviamente li riconosciamo, sono loro, i Fibonacci! Pertanto, abbiamo scoperto che:
    (39)
    La sequenza dei convergenti a Φ è così fatta:
    per ogni k > 1
    Ck-2 = Fk/Fk-1
    Immediatamente cosegue che:
    (40)
    Sia Fk il k-esimo numero di Fibonacci, con k > 1:
    1) La successione Fk/Fk-1 converge alla sezione aurea Φ
    2) Le frazioni Fk/Fk-1 sono le migliori approssimazioni possibili a Φ
    Poiché i quozienti parziali della FC di Φ sono tutti 1, da quanto detto sopra risulta immediatamente che tra tutti i numeri irrazionali Φ è quello che viene approssimato più lentamente dai suoi convergenti!

    Per questo motivo alcuni chiamano Φ il più irrazionale dei numeri. Altri, poiché Φ si lascia avvicinare meno facilmente di qualsiasi altro, lo chiamano il più nobile degli irrazionali.

    6 - I numeri di Fibonacci e i numeri primi

    I numeri di Fibonacci appaiono nelle soluzioni di moltissimi problemi combinatoriali e generano infinite e meravigliose identità aritmetiche.

    Ecco alcune delle loro proprietà:

    (41)
    1) F1 + F2 + F3 + ... + Fn = Fn+2 - 1
    2) F12 + F22 + F32 + ... + Fn2 = FnFn+1
    3) F1 + F3 + F5 + ... + F2n-1 = F2n
    4) Fn-1 Fm+1 - Fn2 = (-1)n
    5) Se m divide n, allora Fm divide Fn
    Dalla (41.4) si deduce immediatamente che due Fibonacci consecutivi sono sempre coprimi, cioé non hanno divisori diversi da 1 in comune.

    La (41.5) è molto interessante: evidenzia un legame tra la divisivilità degli indici e quella dei relativi Fibonacci. Da essa si ottiene:

    (42)
    Se Fn è primo, allora n = 4, oppure n è primo.
    Purtroppo il viceversa della (42) non vale, per esempio
    F19 = 1921 = 13 · 113
    Attualmente è noto che Fn è primo per i seguenti valori di n:
    n = 3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571, 2971, 4723, 5387, 9311, 9677, 14431, 25561, 30757, 35999, 81839
    Rimane aperta la seguente
    (43) Congettura:
    Fn è primo per infiniti indici n
    Una delle caratteristiche più interessanti dei Fibonacci è che
    (44)
    Dato un qualsiasi primo p, esiste un n tale che p divide Fn
    Dalla (44) e dalla (41.5) segue subito che
    (45)
    Dato un qualsiasi primo p, p divide infiniti Fn
    E' spontaneo chiedersi: dato il primo p, come trovare esplicitamente un n tale che p divide Fn? A questa domanda sappiamo rispondere!
    Ricordiamo che
    Con a mod n si denota il resto della divisione di a per n
    Esempi: 10 mod 3 = 1, 10 mod 5 = 0, 15 mod 6 = 3, ...
    (46) Teorema
     Supponiamo p primo.
    p divide Fp-1 se p mod 5 =1 o p mod 5 = 4, altrimenti p divide Fp+1
    Per esempio:
    ....
    17 divide F18 = 23·17·19, perché 17 mod 5 = 2
    19 divide F18, perché 19 mod 5 = 4
    23 divide F24 = 25·32·7·23, perché 23 mod 5 = 3
    ....

    Esiste una importante generalizzazione dei numeri di Fibonacci:

    (47)
    Diciamo successione lineare ricorsiva di grado 2 (abbreviato con SLR), una sequenza di numeri an così definita:
    a0 = A,
    a1 = B,
    an+2 = P an+1 + Q an
    dove A, B, P, Q sono numeri assegnati.
    La successione dei Fibonacci è una SLR con parametri
    A = 0, B = 1, P = 1, Q = 1
    Una delle più notevoli SLR è la seguente, che denotiamo con L, dovuta a Lucas:
    (48) Definizione della successione L
    L è la SLR di parametri A = 2, B = 4, P = 4, Q = -1
    I primi 20 termini di L sono:
    2, 4, 14, 52, 194, 724, 2702, 10084, 37634, 140452, 524174, 1956244, 7300802, 27246964, 101687054, 379501252, 1416317954,5285770564, 19726764302, 73621286644, 274758382274
    La sequenza L è intimamente legata ai numeri perfetti attraverso i numeri primi di Mersenne.
    I numeri perfetti appassionavano i matematici di 2500 anni fa, e sono anche oggi oggetto di attive ricerche.
    (49) Definizione di numero perfetto
    Un numero n si dice perfetto
    se la somma dei suoi divisori     (compreso se stesso) è uguale a 2n.

    Per esempio :
    12 = 1 + 2 + 3 + 6,
    56 = 1 + 2 + 4 + 7 + 14 + 28,
    992 = 1 + 2 + 4 + 8 + ... + 496.
    I primi quattro numeri perfetti sono 6, 28, 496 e 8128.

    Sono noti 41 numeri perfetti, tutti pari. Malgrado recenti tentativi di dimostrazione, rimane aperta la:
    (50) Congettura
    Non esistono numeri perfetti dispari
    Per elencare i 41 numeri perfetti noti ci vorrebbe un volume di centinaia di pagine, perché i più grandi di essi hanno milioni di cifre! E' possibile però identificarli esattamente, mediante i numeri primi di Mersenne.
    (51) Definizione di numero di Mersenne
    diciamo n-esimo numero di Mersenne l'intero
    Mn = 2n - 1
    (52)
    diciamo primo di Meresenne un numero di Mersenne primo.
    Si vede facilmente che:
    (53)
    Mn è primo solo se n è primo
    Purtroppo non vale il "se e solo se". Per esempio:
    M11 = 23·89.
    Tra l'insieme dei numeri perfetti pari e l'insieme dei primi di Mersenne esiste una corrispondenza biunivoca, espressa dal:
    (54) Teorema
    N è un numero perfetto pari se e solo se:
    N = Mp 2p-1 con Mp è primo
    Dunque, come si fa a trovare i numeri perfetti pari? Si cercano i primi di Mesenne Mp.
    Ma, come si fa a vedere se, dato il primo p, Mp è effettivamente primo?
    La risposta a questa domanda segna anche la fine di questa nostra breve avventura matematica. E' uno splendido teorema che lega in modo indissolubile la sequenza L di Lucas ai primi di Mersenne, e quindi ai numeri perfetti:
    (55) Teorema
    Mp è primo se e solo se
    Mp divide Ln
    con n = 2p-2