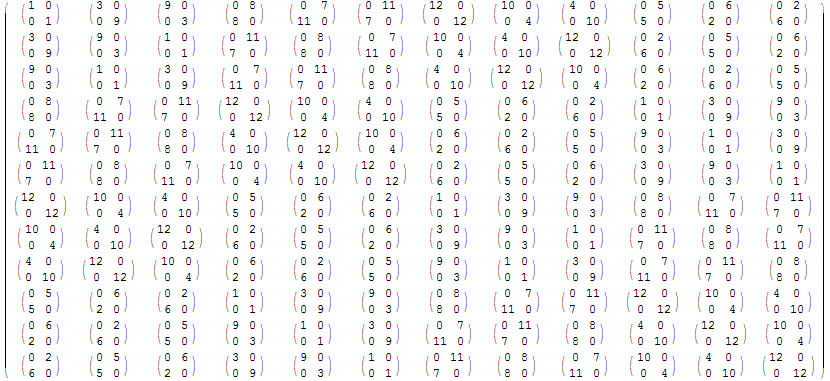Se la casella di partenza è vuota, lo stato di partenza è 1 e a destra della casella di partenza ci sono tutti blank, allora la testina procede all'infinito verso destra, e la macchina non si ferma mai.
Esaminiamo ora attentamente questo programma:
[7]
1,_,2,1,<
2,_,3,1,<
3,_,4,1,<
4,_,4,1,>
4,1,H,1,<
La macchina T deve avere almeno 4 stati e A deve contenere almeno 1.
Supponiamo che T parta nello stato 1 su nastro vuoto. Seguiamo il ragionamento di T:
- Sono nello stato 1 e leggo blank, allora passo nello stato 2, scrivo 1 e vado a sinistra
- Sono nello stato 2 e leggo blank, allora passo nello stato 3, scrivo 1 e vado a sinistra
- Sono nello stato 3 e leggo blank, allora passo nello stato 4, scrivo 1 e vado a sinistra
- Sono nello stato 4 e leggo blank, allora passo nello stato 4, scrivo 1 e vado a destra
- Sono nello stato 4 e leggo 1, allora passo nello stato H, scrivo 1 e vado a sinistra
- Sono nello stato H e non faccio più nulla
Ci sono 5 transizioni. Alla fine sul nastro ci sono 4 uno e la testina è posizionata sull'uno più a sinistra.
Ovviamente nel programma il numero 4 non ha nulla di speciale, duque possiamo asserire che:
[8]
Per ogni x intero naturale, esiste una macchina di Turing T(x) tale che
T(x) ha x+1 stati e
fatta partire su di un nastro vuoto termina la computazione
lasciando x+1 uno sul nastro
ed è posizionata sull'uno più a sinistra.
(La macchina appena descritta è T(3))
Le T(x) serviranno nel teorema centrale di questo Blog.
Probabilmente chi non ha mai visto prima queste cose penserà che si tratta di strumenti poco efficaci. Sembra complicato persino scrivere un Turing-programma che sommi due interi. L'idea di Turing invece era che le sue macchine sono in grado di eseguire qualsiasi calcolo. Detta così, è una affermazione alquanto imprecisa... Occorre precisarla, per poterla discutere.
Ci limiteremo intanto a calcolare i valori di funzioni f di N in N dove N è l'insieme dei numeri naturali.
Supporremo inoltre che in A ci siano soltanto due simboli, uno e blank.
Ecco ora la definizione precisa che ci serve:
[9]
Diciamo che la funzione
f : N -----> N
è Turing-computabile
se esiste una macchina di Turing T la quale, partendo posizionata sull'uno più a sinistra
di x+1 uno consecutivi inseriti nel nastro vuoto
termina la sua computazione in un numero finito di passi
posizionata sull'uno più a sinistra di f(x) + 1 uno consecutivi.
Vediamo due esempi di funzioni Turing-computabili.
[10]
Macchina T1
1,_,2,1,>
1,1,2,1,<
2,_,1,1,<
2,1,H,1,<
Se provate ad eseguire questo programma, facendo partire la macchina dall'uno più a sinistra di m uno consecutivi vedrete che, esattamente in quattro transizioni, la macchina si fermerà sul primo uno di un blocco di m+2 uno. Risultato: la funzione g che manda un naturale n in n+2 è Turing-computabile. Si noti che per calcolare g(n) bisogna mettere n+1 uno consecutivi sul nastro vuoto e mettere la testina sul primo di essi: n è il numero di uno che compare a destra della testina. Analogamente g(n) è il numero degli uno consecutivi che, al termine del calcolo, compaiono a destra della testina.
Il prossimo esempio è indispensabile per il seguito, si tratta della macchina di Turing, che denotiamo con T2, che manda n nel suo doppio 2n.
[11]
Macchina T2
1,_,4,_,>
1,1,2,_,<
2,_,3,1,>
2,1,2,1,<
3,_,1,1,>
3,1,3,1,>
4,_,4,_,<
4,1,5,_,<
5,_,H,_,>
5,1,5,1,<
Se mettete un solo uno sul nastro, e posizionate la testina su di esso, la T2 eseguirà 9 transizioni, scriverà alcuni uno e poi li cancellerà. Al termine sarà su un uno, nel nastro vuoto, come all'inizio. Questo corrisponde al fatto che due volte zero fa zero... Chiamiamo h la funzione tale che h(n) è 2n. Per calcolare h(3) con T2, dobbiamo mettere la testina su un uno con tre uno alla sua destra, e farla partire. La macchina compirà 48 transizioni e si fermerà sul primo uno di un blocco di 7 uno, asserendo correttamente che h(3) vale 6. Per calcolare h(10) impiega 279 transizioni. E' lungo, ma funziona. Noi qui non siamo interessati alla efficienza, ma semplicemente al fatto che la computazione termini in un numero finito di passi e dia il risultato voluto. Si ricordi che T2 ha 5 stati.
Così come si possono comporre due funzioni (applicarle cioé una dopo l'altra) è possibile eseguire la composizione di due macchine di Turing. Il metodo è semplice. Si scrivono i listati uno dopo l'altro e si rinominano gli stati. Se le macchine sono M1, con m1 stati, e M2, con m2 stati allora la macchina composta M2 · M1, con m1 + m2 stati.
Componiamo, come esempio, le macchine T2 e T1 viste sopra. Il programma di T2 · T1
si ottiene in due fasi. Nella prima fase scriviamo semplicemente i due listati uno dopo l'altro, mettendo T2 sotto T1.
1,_,2,1,>
1,1,2,1,<
2,_,1,1,<
2,1,H,1,<
1,_,4,_,>
1,1,2,_,<
2,_,3,1,>
2,1,2,1,<
3,_,1,1,>
3,1,3,1,>
4,_,4,_,<
4,1,5,_,<
5,_,H,_,>
5,1,5,1,<
La macchina composta avrà 2+5=7 stati. Gli stati di T1 rimarranno 1 e 2, quelli di T2, invece di essere 1, 2, 3, 4, 5 diventeranno 3, 4, 5, 6 e 7. Noi vogliamo che quando la macchina T1 ha finito il suo lavoro (ha calcolato x+2 se l'input era x) passi il risultato a T2, che pertanto calcolerà 2(x+2)=2x+4. Per ottenere questo è sufficiente sostituire lo stato di halt di T1 con il primo nuovo stato, 3 e aggiungere quindi 2 a tutti i numeri che rappresentano gli stati di T2. Si otterrà allora (seconda fase)
Macchina T2 · T1
1,_,2,1,>
1,1,2,1,<
2,_,1,1,<
2,1,3,1,<
3,_,6,_,>
3,1,4,_,<
4,_,5,1,>
4,1,4,1,<
5,_,3,1,>
5,1,5,1,>
6,_,6,_,<
6,1,7,_,<
7,_,H,_,>
7,1,7,1,<
Si noti che, completata la seconda fase, le righe del programma si possono rimescolare come si vuole. Un Turing-programma non dipende dal'ordine in cui sono scritte le istruzioni, ogni volta la macchina cerca la riga che inizia con la coppia formata dallo stato in cui si trova e dal simbolo che legge.
Con un input di 5 uno questa macchina si fermerà dopo 160 transizioni con 14 uno alla destra della testina (14=2·(5+2)).
Qui sotto si trova la macchina T1 · T2.
Macchina T1 · T2
1,_,4,_,>
1,1,2,_,<
2,_,3,1,>
2,1,2,1,<
3,_,1,1,>
3,1,3,1,>
4,_,4,_,<
4,1,5,_,<
5,_,6,_,>
5,1,5,1,<
6,_,7,1,>
6,1,7,1,<
7,_,6,1,<
7,1,H,1,<
Con un input di 5 uno questa macchina si fermerà dopo 98 transizioni con 12 uno alla destra della testina (12=(2·5)+2).
Viene naturale chiedersi: che cosa può calcolare una macchina di Turing?
Una buona notizia è che esiste una Universal Turing Machine (UMT). La UMT è una macchina di Turing proprio come quelle di cui abbiamo parlato, costruita in modo da poter simulare il comportamento di qualsiasi macchina di Turing. Essa riceve in input il codice di una maccina e un input accettabile dalla stessa e restituisce il risultato della computazione. Si può pensare alla UMT come un oggetto del tutto simile al computer (completo di sistema operativo e di apposito software) che avete di fronte.
Per esempio voi scrivete un programmino in Java che moltiplica due numeri interi (grandi quanto volete), prod.java:
import java.math.BigInteger;
class prod {
public static void main(String arg[]){
BigInteger x,y,z;
x=new BigInteger(arg[0]);
y=new BigInteger(arg[1]);
z=x.multiply(y);
System.out.println("risultato = "+z.toString(10));}
}
Lo compilate (suppongo che abbiate installato il supporto java adatto al vostro sistema, completamente gratutito) scrivendo
iavac prod.java
e ottenete il file prod.class. Se ora scrivete
java prod 1234567890 2345678901
ottenete
risultato = 2895899851425088890
Che cosa è accaduto? Il file prod.class (meno di 1k) non è un eseguibile. E' soltanto un codice, come i Turing-programmi. Il vostro computer (lui stesso una UTM) ha attivato (mediante il comando java) la VM (Virtual Machine) java (che è anche lei una UTM) la quale ha fatto girare il programmino che avete scritto, passandole come input la coppia di numeri data. La VM java farà girare qualsiasi programma java, per quanto complesso. La VM java agisce come la UTM: esegue il codice che ha ricevuto come input insieme ai dati. In realtà la UTM teorica è più potente, perché dotata di un nastro (memoria) infinito. Se però si considera che in ogni istante sul nastro c'è solo un numero finito di simboli, la differenza scompare nella ipotesi di potere aggiungere dinamicamente tanta RAM quanto basta alla computazione. La possibilità di allocare dinamicamente la memoria è fondamentale, in quanto non sappiamo a priori di quanta memoria avremo bisogno. Se la macchiana è al fondo del nastro (a sinistra o a destra) dobbiamo potere sempre aggiungere una casella.
La famosa Tesi di Church - Turing asserisce che ogni computazione effettiva eseguibile a partire da un algoritmo è calcolabile da una macchina di Turing.
Una versione più modesta della Tesi di Church - Turing assersce che ogni funzione computabile è Turing-computabile (si veda sopra [9]) .
Naturalmente questa Tesi non è (e non potrà mai essere) un teorema, per il semplice fatto che "funzione computabile" è un concetto non ben definito, al contrario di quello di funzione Turing-computabile. Essa è comunque ampiamente accettata, e possiede conferme formidabili, sia teoriche che pratiche.
Quello che è certo è che qualsiasi funzione f di N in N che sia computabile da un programma che gira sul vostro computer, può essere computata da una macchina di Turing. Vale anche il viceversa, con le cautele dovute alla memoria finita, cui abbiamo accennato.
Adesso siamo in grado di capire meglio l'affermazione contenuta nella frase iniziale (tratta dalla OEIS):
The sequence grows faster than any computable function of n, and so is
non-computable
C'è dunque qualcosa che le macchine di Turing non possono calcolare. Qualcosa che quindi non potremo mai calcolare nemmeno noi, con nessun computer, con nessun linguaggio, con nessun algoritmo!
Invece di provare direttamente la incomputabiltà della funzione S(n) (detta Shift), dimostreremo che è incomputabile una sua stretta parente: la funzione di Rado å(n) (detta funzione Sigma), che si trova nella OEIS come sequenza A028444
Sequence: 0,1,4,6,13
Name: Busy Beaver sequence, or Rado's sigma function: maximum number of 1's that an n-state, 2-symbol, 5-tuple Turing machine can print on an initially blank tape before halting.
Comments: The function Sigma(n) (A028444) denotes the maximal number of tape marks which a Turing Machine (TM) with n internal states and a two-way infinite tape can produce onto an initially empty tape and then halt.
The function S(n) (A060843) denotes the maximal number of steps (shifts) which such a TM can do (it needs not produce many tape marks).
Given that 5-state machines can compute Collatz-like congruential functions (see references under A060843), it may be very hard to find the next term. The sequence is non-computable.
Definiamo adesso la funzione å(n). Consideriamo l'insieme minimale di simboli, con due soli elementi
A = { _, 1}
Diciamo B(n) l'insieme macchine di Turing con n stati e 2 simboli, definite in modo completo, vale a dire che il programma contiene 2n quintuple.
Ovviamente B(n) è finito, e dalla [3] si deduce che il suo ordine è
(4n + 4)2n
Facciamo ora partire le macchine appartenenti a B(n) sul nastro vuoto (pieno di blank), nello stato 1. Alcune di queste si fermeranno e altre no. Diciamo FERM(n) l'insieme delle macchine in B(n) che si fermano, e compiono quindi un numero finito di passi. Data una macchina M che si ferma, diciamo s(M) il numero degli uno che sono sul nastro dopo che la macchina si è fermata. Poiché FERM(n) è finito, esiste il massimo degli s(M), con M che varia in FERM(n). Questo è il numero che ci interessa.
Definizione
å(n) = max { s(M), M Î FERM(n) }
I campioni, che quando si arrestano lasciano sul nastro å(n) uno, vengono chiamati Busy Beavers (castori affaccendati).
E' del tutto ovvio che å(1) = 1, e si può provare senza eccessive difficoltà che å(2) = 4 (Rado 1962). Se si affronta il problema delle macchine con 3 stati le cose si complicano molto. Lin e Rado dimostrarono nel 1965 che å(3) = 6. Per n = 4 bisogna attendere il 1983, anno in cui Brady dimostrò che å(4) = 13. Si sa (Marxen) che å(5) è maggiore o uguale di 4098. Il caso 5 potrebbe essere concluso. E' molto improbabile che si riesca a calcolare å(6). Per ora si sa (Marxen e Buntrock) che è maggiore di 1,29·10865. Tanto per fare un esempio concreto, la seguente macchina a 6 stati:
(Esempio dovuto a Marxen)
1,_,2,1,>
1,1,1,1,>
2,_,3,1,<
2,1,2,1,<
3,_,6,_,>
3,1,4,1,<
4,_,1,1,>
4,1,5,_,<
5,_,H,1,<
5,1,6,1,<
6,_,1,_,<
6,1,3,_,<
fatta partire sul nastro vuoto nello stato 1, esegue 8.690.333.381.690.951 transizioni, poi si ferma lasciando 95.524.079 uno sul nastro.
Affrontiamo ora la dimostrazione (del tutto elementare) della incomputabilità della funzione å(n).
Nello spirito della Tesi di Church - Turing, diciamo incomputanbile una funzione che non sia Turing-computabile. Questa è pertanto la nostra tesi:
Non esiste nessuna macchina di Turing che possa calcolare å(n)
Con il termine funzione, intenderemo sempre una funzione di N in N, come del resto nella discussione fatta sulle funzioni Turing-computabili.
Definizione
Diciamo che una funzione f è crescente se
x £ y implica
f(x) £ f(y)
Lemma
Se f è una funzione Turing-computabile, allora
esiste una funzione F crescente e Turing-computabile tale che
per ogni n, f(n) £ F(n)
Dimostrazione
Se f è Turing-computabile evidentemente anche la funzione somma F
F(n) = f(0) + f(1) + f(2) + ... + f(n)
è Turing-computabile.
Inoltre F è crescente, perché f(n) non è mai negativo.
Teorema (Rado)
La funzione å(n) è incomputabile.
Dimostrazione
Per brevità scriviamo computabile al posto di Turing-computabile.
Dimostreremo che se f è una qualsiasi funzione computabile allora
per n sufficientemente grande si ha sempre å(n) > f(n).
Sia allora f una arbitraria funzione computabile e sia M una macchina con c stati
che computa la funzione F introdotta nel Lemma.
Per ogni x sia T(x) la macchina definita in [8].
Si consideri inoltre la macchina T2 definita in [11].
Sappiamo che le macchine si possono comporre.
Sia C la composizione M·T2·T(x).
Poiché M ha c stati, T2 ha 5 stati e T(x) ha x+1 stati,
la macchina composta C possiede c + x + 6 stati.
Facciamo partire C nello stato 1 sul nastro vuoto. La macchina T(x) agisce per prima,
scrive x+1 uno e si ferma sul più a sinistra. Poi passa il controllo a T2.
T2 riceve il numero x in input, quindi al termine si trova sull'uno più
a sinistra di un blocco di 2x+1 uno consecutivi, e passa il suo output 2x a M.
M calcola F(2x) e quindi, in base alla definizione [9], scrive
F(2x) + 1 uno sul nastro vuoto e poi si ferma a sinistra del blocco.
Riassumiamo: C si ferma e possiede c + x + 6 stati.
Quindi C appartiene a FERM(c+x+6).
Con le notazioni precedenti s(C) = F(2x) + 1 e, per definizione di å(n),
avremo che s(C) £ å(c+x+6), il ché implica
(i) F(2x) < å(c+x+6).
Questa diseguaglianza vale per ogni naturale x.
Ora se c + 6 £ x abbiamo c + x + 6 £ 2x,
e conseguentemente, poiché F è crescente
(ii) F(c+x+6) £ F(2x)
Poniamo n = c + x + 6. Se n > 12 + 2c allora x > c + 6
e valgono simultaneamente la (ii) e la (i):
F(n) £ F(2x) < å(n).
Infine, ricordando che per costruzione f(n) £ F(n) si ha che,
per n sufficientemente grande,
f(n) < å(n).
Questo vale per ogni funzione computabile, quindi
å(n) non è computabile.
Si noti che il teorema di Rado dice qualcosa di molto preciso. Se avete una qualsiasi funzione computabile crescente F, e la macchina di Turing che la calcola ha c stati, allora per ogni n maggiore di 12 + 2c, å(n) è maggiore di F(n).
Inoltre il teorema di Rado dice che non solo å(n) non è computabile, ma che non è computabile nessuna funzione che sia (per n abbastanza grande) maggiore di å(n).
Alla luce di questo risultato possiamo rispondere alla domanda iniziale. La funzione Shift S(n) conta il numero di movimenti compiuto dalla macchina. Questo numero è evidentemente maggiore o uguale al numero degli uno che la macchina puà lasciare sul nastro (in partenza vuoto). Pertanto:
Per ogni n, å(n) £ S(n).
Quindi per il teorema di Rado S(n) non è computabile,
e cresce più velocemente di qualsiasi funzione computabile.
Rimangono un paio (almeno) di domande. FERM(n) è formato dalla macchine con n stati che si fermano quando vengano fatte partire sul nastro vuoto nello stato1. FERM(n) è ben definito, una macchina si ferma o non si ferma. Data la macchina T con n stati, possiamo decidere, osservando il suo codice, se appartiene a FERM(n) o meno? E poi che cosa sono le "Collatz-like congruential functions", e che cosa hanno a che fare con la difficoltà di calcolare S(5)? Parleremo di questo nel prossimo Blog. A presto (spero :)!
Comunicate problemi, soluzioni, novità, url interessanti, critiche, suggerimenti, domande, correzioni inviandomi una lettera!. Nel soggetto inserite 'mathblog'.
25 Ottobre 2004
Felici 100k sequenze a Neal J. A. Sloane!

|
Neal J. A. Sloane, membro dello staff dei laboratori di ricerca della AT&T, è certamente uno dei matematici più noti e importanti di questo tempo. Autore di circa 300 lavori e di una ventina di libri è tra i massimi esperti mondiali di teoria dei codici correttori, un settore di enorme importanza per le telecomunicazioni. Nel suo sito si trova moltissimo materiale, articoli, tavole, cataloghi e persino un softaware (Gosset) in grado di minimizzare funzioni di migliaia di variabili vincolate da equazioni o disequazioni lineari! Maestro dell'arte combinatoria, Sloane non si sente costretto dalle possibili applicazioni delle teorie matematiche, ma liberamente insegue ciò che lo affascina, trovando spesso risultati profondi e inaspettati.
Nel dicembre del 1963, studente alla Cornell University, iniziò la sua splendida collezione di successioni di interi, raccolte ora nella On-Line Encyclopedia of Integer Sequences ( OEIS ) |
A quell'epoca Sloane studiava i percettroni (evolutisi poi nelle attuali reti neurali). Lo studio teorico di queste strutture conduce subito a molti difficili problemi di teoria dei grafi. Uno di questi era il calcolo della altezza attesa di un generico nodo quando si prenda a caso un n-albero etichettato radicato (ovvero un grafo non orientato, connesso e senza cicli con n nodi numerati da 1 a n, ed un nodo selezionato detto radice). Per ottenere una sequenza di interi Sloane cercava di calcolare, invece delle effettive altezze medie, gli interi
Wn = an/n
dove an è la somma delle altezze di tutti i nodi su tutti gli alberi. I primi Wn (per n = 1, 2, 3, 4, 5, 6, 7) sono
0, 1, 8, 78, 944, 13800, 237432
Sloane desiderava confrontare la crescita dei Wn con quella di nn. La decina di termini che era riuscito a calcolare non era assolutamente sufficiente. In libri e articoli di combinatoria aveva trovato diverse successioni che somigliavano alla sua, e cominciò a conservarle su schede perforate, pensando che gli sarebbero state utili nella soluzione di altri problemi: le avrebbe riconusciute, avrebbe saputo subito chi erano e che cosa significavano.
Solo nel 1969 Sloane riuscì, con J. Riordan, a esprimere i Wn in "forma chiusa":

Questa successione rimase "scolpita nella memoria" di Sloane, per usare le sue stesse parole, ed attualmente è la A000435 nella OEIS.
In seguito Sloane constatò che la sua raccolta interessava molti matematici, e nel 1973 pubblicò la prima edizione di "A Handbook of Integer Sequences" (che sono orgoglioso di possedere), contenente 2400 sequenze di interi. Seguì nel 1995 (con l'aiuto di Simon Plouffe) "The Encyclopedia of Integer Sequence", ricca di 5500 esemplari. Poi passò alla rete, e Internet portò ad una crescita di circa 10000 successioni all'anno, tanto che nel 1999 la OEIS conteneva circa 50000 successioni.
Oggi ci sono 99277 schede nell'immenso database di Sloane. Neal attende con gioia l'arrivo della 100000-esima sequenza, ed invita tutti gli appassionati ad una festa virtuale!
L'enciclopedia delle sequenze costituisce senza alcun dubbio uno degli ambienti matematici più interessanti del mondo. Voluta fortemente da un singolo ma diventata opera collettiva, è al tempo stesso un prezioso strumento di lavoro e una inesauribile sorgente di avventure numeriche. Vorrei, in questa e in alcune delle prossime puntate del Blog Matematico, percorrere con i lettori alcuni sentieri di questa grande foresta, piena di sorprese.
Cominciamo subito.
Ecco una sequenza, la A000001, che certamente interesserà gli studenti di Matematica o chiunque conosca il concetto di gruppo:
A000001
1, 1, 1, 2, 1, 2, 1, 5, 2, 2, 1, 5, 1, 2, 1, 14, ...
Al posto n c'è il numero dei gruppi di ordine n non isomorfi.
Per apprezzare meglio ricordiamo alcune notazioni e alcuni teoremi:
Notazioni:
Zn denota il gruppo ciclico additivo degli interi modulo n.
Sn è il gruppo delle permutazioni su n simboli (viene chiamato gruppo simmetrico).
Dn è il gruppo delle simmetrie del poligono regolare con n lati (viene chiamato gruppo diedrale).
Teoremi:
1) Se p è primo esiste un solo gruppo di ordine p, isomorfo a Zp.
2) Se p è primo esistono due gruppi di ordine p2: Zp× Zp e Zq con q = p2.
3) Se p è un primo dispari esistono due gruppi di ordine 2p : Z2p e Dp.
4) Se p e q sono primi dispari tali che p < q e p non divide q-1,
allora esiste un solo gruppo di ordine pq, isomorfo a Zpq.
L'inizio della A000001 (1, 1, 1, 2, 1, 2) dice che esistono 1 gruppo di ordine 1, 1 gruppo di ordine 2, 1 gruppo di ordine 3, 2 gruppi di ordine 4, 1 gruppo di ordine 5, 2 gruppi di ordine 6. Fino a 5 tutti i gruppi sono abeliani (cioé commutativi). Quando n = 6 appare il primo gruppo non abeliano: D3 (che è isomorfo a S3).
Nella tavola n varia da 1 a 16, ed i teoremi citati spiegano l'elenco per tutti gli n tranne che per n = 8, 12 e 16. Nel caso di ordine 8 ci sono 5 gruppi, 3 abeliani e 2 non abeliani:
1 - Z2×Z2×Z2
2 - Z2×Z4
3 - Z8
4 - D4
5 - Il gruppo dei quaternioni Q
Rispetto ai gruppi incontrati prima, Q è una novità assoluta!
Denotiamo gli elementi di Q con ±1, ±i, ±j, ±k.
La moltiplicazione in Q è definita dalle seguenti regole:
1 è l'elemento neutro.
Il quadrato di ogni elemento è 1.
ij = k; jk = i; ki = j;
ji = -k; kj = -i; ik = -j;
Anche per n = 12 ci sono 5 gruppi, 2 abeliani e 3 non abeliani:
1 - Z2×Z6
2 - Z12
3 - D6
4 - A4, il sottogruppo delle permutazioni pari di S4
5 - T, prodotto semidiretto di Z3 e di Z4
Il gruppo T si può rappresentare con 12 matrici 2×2 complesse (si veda Math World). Utilizzando il fatto che il gruppo delle radici complesse 12-esime dell'unità è isomorfo al gruppo degli invertibili nell'anello Z13, è possibile descrivere T come gruppo generato dai prodotti modulo 13 di queste due matrici
| 0 8 | | 3 0 |
A = | | , B = | |
| 8 0 | | 0 9 |
La tavola del prodotto è nella figura sottostante, dove la prima riga e la prima colonna sono formate dalle 12 matrici
I, B, B2, A, AB, AB2, A2, A2B, A2B2,A3, A3B, A3B2
Si ricordi che le moltiplicazioni delle matrici contenute nella tavola sono tutte calcolate modulo 13.
Il caso n = 16 è parecchio più complesso, ci sono 14 gruppi, 5 abeliani e 9 non abeliani. Possiamo subito scrivere i 5 abeliani e 3 dei non abeliani:
1 - Z2×Z2×Z2×Z2
2 - Z2×Z2×Z4
3 - Z4×Z4
4 - Z2×Z8
5 - Z16
6 - D8
7 - Z2×D4
8 - Z2×Q
I rimanenti 6 sono più complicati da descrivere e il lettore interessato li può trovare su Math World.
Sono noti (almeno) i primi 2000 termini della successione A000001 (si veda The Small Group Library). Per n fino a 2000 si sa non solo quanti gruppi ci sono di ordine n, ma anche quali sono (cioè come costruirli), con l'unica eccezione di n = 1028. Per n = 1028 esistono ben 49487365422 gruppi diversi!
Il numero dei gruppi di ordine 2k appare singolarmente grande e sembra crescere in un suo modo particolare. I valori noti si trovano nella OEIS al numero A000679 (parte con k = 0):
A000679
1, 1, 2, 5, 14, 51, 267, 2328, 56092, 10494213, 49487365422
Si osservi che anche i (quasi) dieci milioni e mezzo di gruppi di ordine 512 sono noti! Essi sono contenuti, tra milioni di altri, nelle librerie di GAP. GAP (Groups, Algorithms, Programming - a System for Computational Discrete Algebra) è un meraviglioso programma assolutamente gratuito, che gira praticamente su tutte le piattaforme (incluso Windows).
Tra le keywords della A000679 si trova hard: nessuno attualmente conosce quanti gruppi esistano di ordine 211.
Il numero dei gruppi non abeliani di ordine n è difficile da calcolare. Per quanto riguarda i gruppi abeliani finiti, esiste invece una formula. E' molto interessante, perché mostra che i gruppi abeliani finiti si comportano in modo simile ai numeri interi! Per capirla occorre un concetto di grandissima importanza, quello di partizione di un intero (positivo) n.
Diciamo partizione di n una successione non decrescente di interi positivi
h1, h2, ..., ht
tale che la somma dei suoi elementi sia n.
Per esempio, ci sono 7 partizioni di 5:
1, 1, 1, 1, 1
1, 1, 1, 2
1, 1, 3
1, 2, 2
1, 4
2, 3
5
Denotiamo con part(n) il numero delle partizioni di n. Sembra che part(1), part(2), ..., part(n), ... sia una successione interessante. Infatti la troviamo subito nella OEIS, è il numero A000041 (inizio con n = 1)
A000041
1, 2, 3, 5, 7, 11, 15, 22, 30 ,42, 56, 77, 101, 135, 176, 231, 297, 385
Ricordiamo ora che sussiste un teorema:
Teorema 1
Supponiamo che G sia un gruppo abeliano di ordine n, e che n si fattorizzi così:
n = p1e1 · p2e2 · · · pkek, con i pj primi.
Allora G si spezza nel prodotto diretto di k gruppi abeliani Gj, dove Gj ha ordine pjej.
E' sufficiente allora classificare e contare i gruppi abeliani il cui ordine sia la potenza di un numero primo. A questo serve il Teorema 2:
Teorema 2
Un gruppo abeliano H di ordine pm con p primo è prodotto diretto di gruppi ciclici Ci
dove Ci ha ordine phi, con i che varia da 1 a t e
h1, h2, ..., ht è una partizione di m
Esistono dunque part(m) gruppi abeliani di ordine pm.
Mettendo insieme i risultati si ottiene subito il Teorema 3:
Teorema 3
Se l'intero positivo n si fattorizza come nel Teorema 1 allora esistono
part(e1) · part(e2) · · · part(ek) gruppi abeliani con n elementi.
Questi gruppi si possono costruire tutti con il metodo del Teorema 2.
Il bello di questi teoremi è che sono costruttivi, e si possono utilizzare direttamente, anche senza conoscere la loro dimostrazione.
Come esempio, vediamo quanti e quali sono i gruppi abeliani di ordine 324.
Esempio.
In primo luogo fattorizziamo n = 324.
324 = 22 · 34.
Per il Teorema 1, se G è abeliano con 324 elementi si ha che
G è isomorfo a G1 × G2, dove G1 ha 4 elenemti e G2 ha 81 elementi.
Applichiamo ora il Teorema 2.
Ci sono 2 partizioni di 2:
1, 1
2
e 5 partizioni di 4:
1, 1, 1, 1
1, 1, 2
1,3
2,2
4
Esistono pertanto 2 gruppi abeliani di ordine 4 che possono essere G1
Primo gruppo G1:
Z2 × Z2
Z4
Esistono inoltre 5 gruppi abeliani di ordine 81 che possono essere G2
Secondo gruppo G2:
Z3 × Z3 × Z3 × Z3
Z3 × Z3 × Z9
Z3 × Z27
Z9 × Z9
Z81
I 10 gruppi di ordine 324 si trovano facendo i prodotti, in tutti i modi,
di un gruppo tipo G1 con un gruppo tipo G2.
Per n non troppo grande sappiamo quindi calcolare il numero dei gruppi abeliani di ordine n. Questa successione è la A000688 della OEIS.
A000688
1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 1, 2, 1, 1, 1 , 5, 1, 2, 1, 2, 1, 1, 1,3 , 2, 1, 3, 2, 1, 1
Al contrario della A000679 questa successione è easy. Possiamo prevedere i suoi valori. Sappiamo, per esempio, che al posto 324 c'è 10.
Nel prossimo blog un'altra gita nella OEIS (che avrà, auguriamo, gioiosamente superato le 100k sequenze)!
Comunicate problemi, soluzioni, novità, url interessanti, critiche,
suggerimenti, domande, correzioni inviandomi una
lettera!. Nel soggetto inserite 'mathblog'.
18 Settembre 2004
Congettura di Riemann e sicurezza mondiale
Sul numero di settembre di Le Scienze c'è un interessante articolo di Graham P. Collins sulla dimostrazione, da parte del matematico russo Grigory Perelman, della famosa congettura di Poincaré. Si tratta - come viene spiegato sulla stessa rivista - di uno dei sette "problemi del millennio", pubblicati sul sito del Clay Mathematics Institute. Per ognuno di essi viene offerto al solutore un premio di un milione di dollari.
Tra i magnifici sette appare, e non poteva essere altrimenti, la congettura di Riemann, più frequentemente detta ipotesi di Riemann. Il matematico Louis de Branges de Bourcia, che lavora presso la Purdue University, sostiene di avere provato la verità dell'ipotesi di Riemann, ma la comunità degli esperti non è completamente convinta della validità della dimostrazione.
Sembra, dai commenti della stampa internazionale, che la possibilità dell'esistenza della dimostrazione, faccia paura. Qualche esempio:
Solution to arcane maths problem leads to doomsday projections
11 Settembre 2004, The Times of India. (Copia locale)
Math problem solved=No Net transaction safe
7 Settembre 2004, Hindustan Times (Copia locale)
Maths holy grail could bring disaster for internet
7 Settembre 2004, Guardian (Copia locale)
Vorrei cercare di spiegare, per quanto possibile brevemente e in modo semplice, da dove nascono questi timori e fino a che punto essi siano giustificati.
Dalla matematica salvezza e perdizione
Tutto il commercio elettronico ed i rapporti tra banche si fondano sulla crittografia. Quando, per esempio, acquistiamo qualcosa in rete, veniamo inseriti in un canale particolare, sicuro. Il male intenzionato che riuscisse ad intercettare il documento che inviamo al server non sarebbe in grado di decifrare il numero della nostra carta di credito, perché esso è stato crittato. Tutti i codici classici si basano su una chiave segreta. Il vostro computer ed il server ospite si scambiano una chiave, che viene creata sul momento, nuova ogni volta. Per passarsi la chiave occorre evidentemente un protocollo di trasmissione che metta in cifra il messaggio senza avere a sua volta bisogno di effettuare uno scambio di chiavi, altrimenti si entrerebbe in un circolo vizioso. I metodo usati in questa prima ed essenziale fase vengono detti cifrari a chiave pubblica. Nel caso di un cifrario a chiave pubblica, chiunque può conoscere la chiave: non riuscirà lo stesso a rompere il codice.
In sostanza, tralasciando diverse altre componenti troppo tecniche, in una transazione commerciale on-line vengono utilizzati due codici: uno standard (si dice simmetrico) che necessita di una chiave segreta ed è molto veloce, l'altro a chiave pubblica, in genere più lento perché esegue calcoli pesanti. Per esempio, come codice simmetrico si potrebbe usare l'AES (Advanced Encription Standard) e come codice a chiave pubblica l'RSA (acronimo dei nomi dei suoi inventori: Rivest, Shamir e Adleman). Il lettore che desideri chiarimenti in proposito può consultare, in questo stesso sito, le pagine su Crittografia e numeri primi.
E' chiaro che se si rompe il codice a chiave pubblica, il quale custodisce la chiave del codice simmetrico, tutto viene a cadere.
Uno degli algoritmi più usati è proprio lo RSA. La sua forza si basa sul fatto che
1) E' facile trovare numeri primi grandi
2) E' difficile fattorizzare un intero prodotto di due numeri primi grandi
Ovviamente il termini "facile", "difficile" e "grande" sono relativi alla conoscenza scientica e alla tecnologia disponibili. Attualmente sono grandi primi di alcune centinaia di cifre decimali. Facile rappresenta un tempo di secondi e difficile di secoli.
Concludendo: l'intero sistema di sicurezza mondiale entrerebbe in gravi difficoltà se qualcuno trovasse un algoritmo veloce per la fattorizzazione di interi.
Che cosa c'entra tutto questo con la congettura di Riemann? Sentiamo le parole del professor Marcus du Sautoy, autore di un bestseller pubblicato in Italia da Rizzoli, con il titolo "L'enigma dei numeri primi":
L'intero commercio elettronico dipende dai numeri primi. Io ho descritto i primi come atomi: ciò che manca ai matematici è uno spettrometro di primi. I chimici hanno una macchina che, se ci mettete una molecola, vi dice di quali atomi è composta. I matematici non hanno inventato una versione analoga di essa. Se l'ipotesi di Riemann è vera, essa non produrrà di per sé uno spettrometro. Ma la sua dimostrazione potrebbe farci capire meglio il funzionamento dei numeri primi, e quindi la dimostrazione potrebbe essere trasformata in qualcosa che potrebbe produrre questo spettrometro di primi. Se ciò accadrà, metterà in ginocchio l'intero commercio elettronico nello spazio di una notte.
Si tratta di affermazioni prudenti, piene di "se" e "potrebbe". Ma la stampa, con la sua solita sensibilità, si è lanciata con entusiasmo nell'impresa di spaventare gli utenti, prospettando un futuro prossimo in cui utilizzare bancomat e carte di credito sarà impossibile.
In uno degli articoli citati si legge:
Fino a che i numeri primi erano considerati casuali, poteveno essere utilizzati senza problemi nelle moderne applicazioni di cifratura dei dati, che vanno dalle transazioni bancarie e il commercio elettronico all'uso delle carte di credito e al trasferimento di denaro su Internet. Una volta che la casualità sia provata falsa, però, finirà la cuccagna, nessun codice sarà più sicuro e nessuna transazione sarà protetta da intrusioni fraudolente. Alcuni pensano che per l'economia questo potrebbe essere l'equivalente di un asteroide che colpisca la Terra.
Siamo all'apocalisse! La matematica ha creato il paradiso della sicurezza informatica, dei codici inviolabili, e ora vuole distruggerlo! Ma, alla fine, che cosa dice mai questa congettura di Riemann?
La congettura di Rieman e le sue gemelle
Nel seguito denoteremo la congettura di Riemeann con l'abbreviazione usuale RH, che sta per Riemann Hypothesis.
Per esprimere la RH occorre introdurre la funzione z, detta funzione zeta di Riemann (di z si è già parlato in un Blog precedente: Pi greco e i numeri primi). Essa è così definita:
z(s) = å n-s
dove nella sommatoria n varia da 1 all'infinito,
e s è un numero complesso con parte reale maggiore di 1.
Il legame di z con i numeri primi è dato dal prodotto di Eulero:
(D)
z(s) = Õ (1 - q-s)-1
dove q varia nell'insieme dei numeri primi
e s è un numero complesso con parte reale maggiore di 1.
La funzione z(s) è stata poi estesa da Riemann a tutto il piano complesso (tranne che in s=1, dove ha una singolarità).
Possiamo ora enunciare la RH (che riguarda la estensione di z):
Gli zeri complessi di z(s) hanno tutti parte reale = 1/2.
Gli zeri complessi di z formano un insieme numerabile e discreto. Per ragioni di simmetria è sufficiente esaminare quelli con parte immaginaria positiva, sopra l'asse delle ascisse. Si trovano un primo zero, un secondo, un terzo... La RH dice che essi sono tutti della forma
1/2 + b I
dove I è l'unità immaginaria, cioè I2 = -1
I primi sei zeri che si trovano hanno parte reale uguale a 1/2 e parte immaginaria (approssimata) b rispettivamente uguale a
14.134725, 21.022040, 25.010858, 30.424876, 32.935062, 37.586178
Sono stati calcolati più di 100 miliardi di zeri consecutivi e la RH è provata per b < 29538618432. Molti zeri sono vicinissimi, difficili da separare. Il calcolo degli zeri di z è assai delicato e richiede metodi matematici sofisticati.
Nel 1914 Hardy dimostrò che infiniti zeri stanno sulla "retta critica", x = 1/2.
Nel 1989 Conrey provò che almeno il 40% degli zeri sta sulla retta critica.
Malgrado questo la RH potrebbe benissimo essere falsa!
Esistono molte formulazioni della RH, ad essa logicamente equivalenti, ma in apparenza totalmente diverse!
Ne vedremo insieme quattro, che denoteremo con RH1, RH2, RH3, RH4.
Una qualunque di esse è vera (o falsa) se e solo se è vera (o falsa) la RH.
Iniziamo con quella che mi sembra la più comprensibile da parte dei non addetti ai lavori, dovuta a Lagarias (2000). La chiamo RH1.
RH1
Denotiamo con Hn la somma degli inversi dei primi n interi positivi:
Hn = 1 + 1/2 + 1/3 + ... + 1/n.
Denotiamo con s(n) la somma dei divisori di n.
La RH è equivalente al fatto che, per ogni n maggiore di 1
s(n) < Hn + eHn log(Hn)
dove log è il logaritmo naturale, in base e.
Per capire che cosa dice la RH1 vediamo un caso particolare. Poniamo n = 20.
Troviamo H20 = 3.59774, e3.59774 = 36.5156, log(3.59774) = 1.28031,
s(20) = 42.
Allora RH1 è confermata per n = 20 in quanto
42 < 3.59774 + 36.5156 ´ 1.28031 = 50.349
Nella figura sottostante vediamo segnate le differenze L(n) = (Hn + eHn log(Hn)) - s(n) per n che varia da 2 a 300
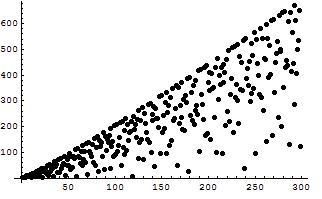
Figura 1
Come si vede, alcuni individui si staccano dalla massa e giungono pericolosamente vicino a 0. Tra 50 e 300 si raggiungono i valori più bassi di L(n) per n=60 e n=120
L(60) = 2.97668
L(120) = 6.06265
RH1 è equivalente a RH, una di esse è vera se e solo se è vera l'altra. Chiunque riuscisse a provare che L(n) è maggiore di 0 per ogni n, cioè che i puntini in figura non vanno mai sotto l'asse delle ascisse, per quanto si estenda il grafico, guadagnerebbe fama imperitura e un milione di dollari!
Si rimane stupiti dall'assenza in RH1 di qualsiasi riferimento esplicito ai numeri complessi o ai numeri primi. Ovviamente il legame esiste, ma è molto nascosto.
Al contrario la RH2, la sconda formulazione della RH che presenteremo, è immediatamente connessa ai primi.
Passeggiare a caso o con Moebius: che differenza c'è?
Cominciamo col definire la funzione m di Moebius
Diciamo che l'intero n è privo di quadrati se n si decompone
nel prodotto di primi distinti.
m è definita sugli interi positivi
m(1) = 1
m(n) = 0 se n non è privo di quadrati
m(n) = 1 se n è prodotto di un numero pari di primi distinti
m(n) = -1 se n è prodotto di un numero dispari di primi distinti
Facciamo un poco di pratica.
Chiamiamo F l'insieme formato dagli interi positivi che sono prodotto di primi distinti. In F troveremo 2, 3, 5, 6 ... , ma non 4, 8, 9, 12 ...
I primi 18 elementi di F
F = { 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30 ... }
Ad ogni intero k in F associamo ora la sua immagine mediante m, cioé m(k). Otteniamo così un nuovo insieme V, in corrispondenza biunivoca con F
I primi 18 elementi di V
V = { -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, 1, -1, -1 ... }
Se si calcolano alcune migliaia di elementi di V, si constata che gli 1 e -1 sembrano messi a caso, come se si trattasse dei risultati del lancio di una moneta.
Per visualizzare il fenomeno ci costruiamo una passeggiata su una retta verticale (l'asse delle ordinate). Chiamiamo questa passeggiata Passeggiata di Moebius. All'inizio (tempo t=0) siamo in 0. Ogni volta, al tempo t, ci muoviamo di m(t) lungo l'asse y: ovvero saliamo di 1 se m(t)=1, scendiamo di 1 se m(t)=-1, stiamo fermi se m(t)=0.
Nella figura sottostante si vede il risultato dei primi 50000 passi.

Figura 2
Sulle ascisse c'è il tempo t da 0 a 50000. In nero la passeggiata di Moebius, in rosso il grafico di ±½Öt, in blu il grafico di ±Öt.
Ricordando che per muoverci ad ogni passo aggiungiamo m(t) al valore della ordinata, deduciamo immediatamente che la linea nera della Figura 2 è il grafico della funzione di Mertens M(t) così definita
M(t) = åm(k)
dove k varia da 1 a t
Dalla Figura 2 sembra che la linea nera stia sempre dentro alla curva rossa. Nel 1897 Mertens congetturò
Mertens Hypothesis (MH)
Per ogni t maggiore di 1 il valore assoluto di M(t) è minore di Öt
Von Sterneck calcolò, tra il 1897 e il 1912 i valori di M(t) fino a t = 5000000, e giunse alla seguente congettura
Per ogni t maggiore di 200 il valore assoluto di M(t) è minore di ½Öt
Quando si tratta della distribuzione dei numeri primi, bisogna sempre essere cauti nelle affermazioni! Il fatto che una proposizione sia vera in milioni di casi non la rende per questo più credibile!
Il primo controesempio (Cohen e Dress, 1979) si ha per t più grande di sette miliardi, precisamente t=7725038629. Infatti
M(7725038629) = 43947
½Ö7725038629 = 43946.09
Anche la congettura di Mertens MH è risultata falsa. Nel 1985 Odlyzko e Riele hanno dimostrato che la linea nera della Figura 2 attraversa la curva blu infinite volte, sia in alto che in basso. Precisamente
il limite inferiore di |M(t)|/Öt è minore di -1.009
il limite superiore di |M(t)|/Öt è maggiore di 1.06
dove | | denota il valore assoluto
Non si conosce però nessun valore di t che fornisca un controesempio alla MH.
Qual è il vero rapporto tra la funzione di Mertens M(t) e la radice quadrata di t Öt ? E' uno dei grandi enigmi legati alla distribuzione dei numeri primi!
Esiste una versione "più moderata" della MH, una congettura che indichiamo con MH'
MH'
Esistono una costante C ed un intero n tali che per t > n si ha
|M(t)| < C Öt
MH implica MH', ma non viceversa. MH è falsa, ma MH' potrebbe essere vera. Al momento nessuno lo sa dimostarare, ma si pensa che anche MH' sia falsa.
Si ritiene vera una versione di MH ancora più debole, che è proprio la seconda formulazione della RH di cui si parlava, la RH2.
L'ipotesi di Riemann RH è vera se e solo se è vera la:
RH2
Dato un qualsiasi e > 0, esiste un intero n tale che per ogni t > n si ha
|M(t)| < te Öt
La RH2 evidenzia un rapporto profondo tra la passeggiata di Moebius e una passeggiata casuale!
Nella Figura 3 si vede una passeggiata casuale, costruita in modo analogo a quella di Moebius vista sopra. All'istante t, se t non è privo di quadrati si sta fermi, come nella passeggiata di Moebius, mentre, quando t è privo di quadrati, si lancia una moneta, invece di considerare il valore della m: si sale di un passo se viene testa, e si scende di un passo se viene croce.

Figura 3
Anche facendo moltissime prove è assai difficile trovare il pacato movimento ondulatorio della Figura 2. Però questo non prova proprio nulla. E' dai fondamenti della probabilità che possiamo avere informazioni sul futuro lontano di una passeggiata casuale. Se ci muoviamo su e giù lanciando una moneta, e denotiamo con D(t) la differenza tra il numero dei casi in cui è venuto testa e quello in cui è venuto croce, vale il teorema
Teorema della distanza
Dati comunque un e > 0 e una probabilità p < 1, esiste un intero n tale che per ogni t > n si ha
|D(t)| < te Öt con probabilità p
Si noti che |D(t)| è la distanza dall'origine, all'istante t, del punto che effettua la passeggiata casuale.
Se è vera la RH, è vera anche la RH2. Il teorema della distanza confrontato con la RH2 ci dice che, se prendiamo e piccolissimo e p molto vicina a 1, per grandi n il comportamento della passeggiata casuale è molto simile a quello della passeggiata di Moebius! Se si va abbastanza avanti, anche il grafico della Figura 3 si troverà confinato all'interno di una zona quasi parabolica, tranne rarissime uscite.
Questa connessione è stata evidenziata da Denjoy nel 1964.
Quanti sono i numeri primi minori di x?
E' una buona domanda, vero? La funzione che conta i primi viene denotata in genere con p:
p(x) = numero dei primi minori o uguali a x
Quindi, per esempio,
p(5) = 3
p(50) = 15
p(500) = 95
p(5000) = 669
p(50000) = 5133
p(500000) = 41538
p(5000000) = 348513
p(50000000) = 3001134
Nel 1896 Hadamard e, indipendentemente, de la Valleé Poussin, basandosi sul lavoro di Riemann provarono il
Teorema dei numeri primi
Il rapporto tra p(x) e x/log(x) tende a 1
quando x tende all'infinito.
Questo significa che, quando x è grande, x/log(x) è una buona approssimazione di p(x). Per esempio, per x=50000000 il valore esatto è 3001134, mentre x/log(x) vale circa 2820470, con una precisione del 93.9%.
Una approssimazione migliore, già suggerita da Gauss, è data dal logaritmo integrale Li(x), dove

Con il programma Mathematica, otteniamo che Li(50000000) vale circa 3001560; confrontando con il valore esatto 3001134 si ha una precisione del 99.9%. L'approssimazione è incredibilmente buona. Possiamo quantificare l'errore Li(x) - p(x)?
Nel 1901 von Koch dimostrò che RH è equivalente alla
RH3
Dato un qualsiasi e > 0, esiste un intero n tale che per ogni t > n si ha
|Li(t) - p(t)| < te Öt
Se proviamo a sommare i logaritmi dei numeri primi, osserviamo che
la somma dei logaritmi dei numeri primi minori o uguali a x è molto vicina a x stesso.
Poniamo q(x) = å log(p)
dove la sommatoria è estesa a tutti i primi minori o uguali a x.
Troviamo:
q(100) = 83.72
q(1000) = 956.24
q(10000) = 9895.99
q(100000) = 99685.4
q(1000000) = 998484
Anche in questo caso, per stimare l'errore commesso, cioé la differenza tra q(x) e x, ci viene in aiuto la RH, in un'altra equivalente formulazione:
RH4
Dato un qualsiasi e > 0, esiste un intero n tale che per ogni t > n si ha
|q(t) - t| < te Öt
A questo punto si può osservare che una dimostrazione della congettura di Riemann avvicinerebbe semplicemente la nostra conoscenza teorica, esatta, alla nostra conoscenza empirica, sperimantale. Empiricamente Li(x) è una approssimazione molto buona di p(x) (e altre funzionano ancora meglio), e nessuno ci impedisce di usarla. Una prova di RH (o equivalenti) fornirebbe semplicemente un dimensionamento certo (ma non necessariamente ottimale) del margine di errore.
La forza è nella verità o nella dimostrazione?
Si ricorderà che alcuni sostengono che l'impatto della dimostrazione di RH sarebbe terribile.
Un tema ricorrente a favore di questo è che "i numeri primi non sarebbero più a caso".
Su questo facciamo tre considerazioni.
La prima è di carattere, direi quasi, ontologico. La sequenza dei primi non può essere in nessun modo casuale, qualsiasi sia il significato che si voglia dare a questa frase, per il semplice fatto che è completamente determinata dalla struttura aritmetica dell'insieme dei numeri interi. Prendete i numeri naturali 1, 2, 3, 4, 5, ..., cominciate a giocare con l'addizione (il prodotto non serve in modo diretto) ed eccoli lì: preziosi, luminosi e belli come le stelle del cielo!
La seconda è che, paradossalmente, la RH sembra puntare in direzione completamente opposta. Abbiamo visto che, se RH è vera, la distribuzione degli interi che sono prodotto di un numero pari di primi o di un numero dispari di primi segue da vicino la distribuzione delle apparizioni di testa o croce in una sequenza abbastanza lunga di lanci di una moneta non truccata. Che cosa c'è di più casuale di questo?
La terza, come la prima, elimina la possibiltà che la successione dei primi sia casuale, perché presenta notevoli regolarità. Ne citiamo due:
(1) Per ogni n, tra n e 2n c'è almeno un numero primo.
(2) Tra n! + 2 e n! + n non ci sono numeri primi.
La affermazione (1) è detta Postulato di Bertrand, matematico che la verificò nel 1845 per n fino a 3000000. Venne dimostrata da Tchebychef nel 1850. Il grande Erdös ne diede una dimostrazione assai elegante e semplice nel 1932. La tecnica di Erdös può essere estesa per dimostrare che dato qualsiasi k esiste un N tale che, se n è maggiore di N, ci sono tra n e 2n almeno k primi.
La (2), sebbene interessante, è ovvia. Ricordiamo che n! è il prodotto degli interi tra 1 e n. Allora n! + 2 è divisibile per 2, n! + 3 è divisibile per 3, e così via fino a n! + n, che è divisibile per n.
Pur essendo poco più di una banalità la (2) dà un'argomentazione fortissima in sostegno della non-casualità della successione dei primi. In una successione casuale esisteranno spazi lunghi quanto si vuole privi di un certo simbolo, ma non sapremo mai dove si trovano.
Dunque, certamente la successione dei primi non è casuale. Però, a partire da essa si generano sequenze con un comportamento apparentemente casuale, e la RH fornisce informazioni asintotiche sulla oscillazione di queste quantità.
Per concludere dirò che ritengo assai improbabile che la dimostrazione della RH possa portare a grandi rivoluzioni nel mondo delle comunicazioni riservate. Questo avverrebbe se - per esempio - facilitasse la fattorizzazione degli interi. Occorre però ricordare che da anni e anni vengono studiate tutte le possibili implicazioni logiche della RH.
Per esempio, è noto che se la RH fosse vera allora un certo test probabilistico di primalità darebbe risultati certi e veloci, mentre ora sono sì veloci ma sicuri solo entro un certo limite, che possiamo fissare. Per esempio un numero di 500 cifre che abbiamo trovato è dichiarato primo con una probabilità di 1 su 10100 di non esserlo. Tutti i programmi di calcolo simbolico, come Maple o Mathematica, utilizzano combinazioni di test di questo genere. La differenza tra la certezza assoluta e la garanzia con probabilità 0.99999999... con cento 9 dopo il punto è, ad ogni effetto pratico, irrilevante.
Il problema della fattorizzazione è diverso. Essa avviene o non avviene, semplicemente. Che io sappia nessuno ha ricavato metodi di fattorizzazione dalla ipotesi che RH sia vera. Non esiste un teorema del tipo
Se vale RH allora, dato un intero N, faccio questo e questo e lo fattorizzo velocemente.
Se esistesse lo si potrebbe usare: se N non si fattorizza nel tempo previsto la RH è falsa; se N si fattorizza siamo felici e rompiamo il codice RSA, anche senza avere dimostrato la RH.
Un teorema può avere un enunciato elegante ed essere esteticamente bello; può avere una dimostrazione difficile e profonda, ed essere per questo di grande interesse matematico. Però la sua forza, la sua efficacia, non sta nella dimostrazione ma nelle sue possibilità di applicazione, nelle conseguenze che da lui si possono trarre, e queste dipendono solo dalla sua verità.
Comunicate problemi, soluzioni, novità, url interessanti, critiche, suggerimenti, domande, correzioni inviandomi una lettera!. Nel soggetto inserite 'mathblog'.
17 Luglio 2004
C'è un limite all'abbondanza?
Ricordiamo la definizione della funzione somma dei divisori di n, che si denota con s(n), già utilizzata nel blog sui numeri amicali del 31 maggio 2003:
s(n) = å d
dove la sommatoria è estesa a tutti i divisori d di n.
Esempi:
s(9) = 1 + 3 + 9 = 13
s(10) = 1 + 2 + 5 + 10 = 18
Dato un intero positivo n si definisce abbondanza di n ( abb(n) ) il rapporto tra s(n) ed n.
Formalmente:
abb(n) = s(n)/n
Esempi:
abb(6) = s(6)/6 = 12/6 = 2
abb(10) = s(10)/10 = 18/10 = 9/5 = 1,8
Se p è primo, i suoi divisori sono 1 e p, dunque s(p) = 1 + p.
Se n è la potenza d un primo, cioè n = pe, allora
s(n) = 1 + p + p2 + ... + pn = (pe+1 - 1)/(p-1)
Inoltre s è una funzione aritmetica moltiplicativa, ovvero
se due interi m ed n non hanno fattori maggiori di 1 in comune,
allora s(m n) = s(m) s(n).
Pertanto se si conosce la fattorizzazione di n, s(n) e - conseguentemente - abb(n) sono facili da calcolare.
Supponiamo che la fattorizzazione di n sia:
n = pm qk ·· rh
con p, q, .. ,r primi, allora
s(n) = ((pm+1 - 1) (qk+1 - 1) ·· (rh+1 - 1)) /((p-1) (q-1) ·· (r-1))
Esempio:
n = 1234567890 = 2 32 5 3607 3803
s(n) = 3 13 6 3608 3804 = 3211610688
abb(n) = 3211610688/1234567890 = 178422816/68587105 = 2,6014
L'unico numero che ha abbondanza 1 è 1 stesso. L'abbondanza di un numero primo p è 1 + 1/p. Quindi abb(p), con p primo, è di pochissimo superiore a 1, se p è grande.
Ricordiamo che n si dice perfetto se n è esattamente la metà della somma dei suoi divisori. In altri termini
n è perfetto se e solo se abb(n) = 2
I primi quattro numeri perfetti sono 6, 28, 496 e 8128.
Esiste un legame tra i numeri perfetti pari ed i numeri primi di Mersenne:
n è un numero perfetto pari se e solo se
n = (2p - 1) 2p-1
con 2p - 1 primo.
Si noti che la primalità di 2p - 1 implica la primalità di p.
Mp = 2p - 1, viene detto primo di Mersenne
Al momento sono noti 41 primi di Mesenne (si veda il blog precedente), e quindi sono noti 41 numeri perfetti pari.
Circa un mese fa (il 14 giugno 2004) Simon Davis ha pubblicato una ingegnosa dimostrazione del fatto che non esistono numeri perfetti dispari.
Si congettura (con molti indizi a favore) che ci siano infiniti numeri perfetti.
Ma, si sa, non tutti sono perfetti... e anche gli interi si dividono in perfetti, abbondanti e deficienti
n si dice abbondante se abb(n) > n
n si dice deficiente se abb(n) < n
Non è difficile provare che
Teorema 1
Se k > 1, allora abb(kn) > abb(n)
Il teorema 1 dimostra in particolare una asserzione che risale al XIII secolo: i multipli dei perfetti sono abbondanti, mentre i divisori dei perfetti sono deficienti.
Per il teorema 1 la successione abb(ph), con p primo e n = 1, 2, 3, ... è strettamente crescente. Questa sucessione però non tende all'infinito ma è limitata. Precisamente:
Teorema 2
abb(ph) = (ph+1 - 1)/(ph+1 - ph)
lim abb(ph) = p/(p-1)
h®¥
Poiché l'abbondanza è moltiplicativa si ottiene subito che, se n è un intero positivo qualsiasi:
Teorema 3
lim abb(nh) = (p/(p-1)) (q/(q-1)) ··· (r/(r-1))
h®¥
dove p, q, r, ... sono i divisori primi di n.
Esempio:
lim abb(10h) = (2/(2-1)) (5/(5-1)) = 2 5/4 = 5/2 = 2,5
h®¥
abb(10) = 1,8
abb(100) = 2,17
abb(10000) = 2,4211
abb(1000000) = 2,48044
abb(100000000) = 2,49512
abb(10^17) = 2,49999
In base al teorema 3, nessun numero da solo può produrre abbondanza illimitata, anche se utilizza tutte le sue infinite potenze. Però non c'è un limite all'abbondanza degli interi, presi nel loro insieme.
Teorema 4
L'abbondanza dei numeri interi non ha un limite superiore.
In particolare dimostriamo che la successione abb(k!) tende all'infinito,
al crescere di k.
Dimostrazione
Se n è divisibile per 1, 2, 3, ..., k ovviamente
s(n) ³ n + n/2 + n/3 + ··· + n/k
Dalla definizione di abbondanza si ha allora che
abb(n) = s(n)/n ³ 1 +1/2 + 1/3 + ··· + 1/k
Al crescere di k la somma 1 +1/2 + 1/3 + ··· + 1/k tende all'infinito
(risultato noto come divergenza della serie armonica),
e ne consegue la tesi.
In base al risultato del Teorema 4, dato un numero positivo M grande a piacere, percorrendo la successione degli interi incontreremo, ad un certo punto, un individuo il quale ha un'abbondanza maggiore di M, ed è il più piccolo che la possiede. Questo signore ha tutta l'aria di essere un campione: la sua abbondanza è più grande di quella di tutti gli interi che lo precedono.
Diciamo che n è superabbondante se
per ogni k minore di n abb(n) > abb(k)
Ecco i primi 24 superabbondanti:
1, 2, 4, 6, 12, 24, 36, 48,
60, 120, 180, 240, 360, 720, 840, 1260,
1680, 2520, 5040, 10080, 15120, 25200, 27720, 55440
con le loro rispettive abbondanze:
1, 1.5, 1.75, 2, 2.33333, 2.5, 2.52778, 2.58333,
2.8, 3, 3.03333, 3.1, 3.25, 3.35833, 3.42857, 3.46667,
3.54286, 3.71429, 3.8381, 3.9, 3.93651, 3.96603, 4.05195, 4.18701
Vi sono numeri - tra i quali i perfetti - la cui abbondanza è un numero intero, essi sono detti multipefetti.
Diciamo che n è multiperfetto se
s(n) = kn, con k intero
k viene detto indice di n
I numeri perfetti sono quelli con indice 2.
Non è facile trovare numeri multiperfetti, e fino a qualche anno fa se ne conoscevano ben pochi.
Il più piccolo multiperfetto non perfetto è 120, che ha indice 3. Si ritiene che per ogni indice k maggiore di 2 esista solo un numero finito di interi multiperfetti con indice k. Si ritiene anche che tutti i multiperfetti di indice minore di 7 siano stati trovati; ce ne sono
6 di indice 3
36 di indice 4
65 di indice 5
245 di indice 6
Sono noti 4676 multiperfetti con indici compresi tra 7 e 10, mentre la teoria ne prevede più di 9000. E' noto un solo intero di indice 11 (ha circa 1900 cifre), e dovrebbero esisterne una decina di migliaia.
Nessun intero multiperfetto con indice maggiore di 11 è noto, se ne trovate uno fatemelo sapere!
Comunicate problemi, soluzioni, novità, url interessanti, critiche, suggerimenti, domande, correzioni inviandomi una lettera!. Nel soggetto inserite 'mathblog'.