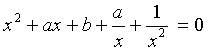
ค่าต่ำสุด (solution by me)
จากสมการ x4 + ax3 + bx2 + ax + 1 = 0
จะเห็นได้ชัดว่า x ไม่เท่ากับ 0 ดังนั้นสามารถนำ x2 หารตลอดได้
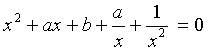
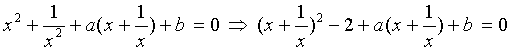
ให้ x + 1/x = m จะได้สมการใหม่คือ
m2 + am + (b-2) = 0
ซึ่งเมื่อแก้สมการกำลังสองนี้จะได้ผลเฉลยคือ

แต่เนื่องจากต้องการให้มี x เป็นจำนวนจริง และความจริงที่ว่าถ้า x เป็นจำนวนจริง
abs(x+1/x) >=2 เสมอ จึงได้ว่า
 ซึ่งก็คือ
ซึ่งก็คือ
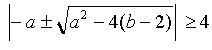
เนื่องจากความจริงที่ว่า |p| + |q| >= | p(+/-)q |
จะได้ว่า
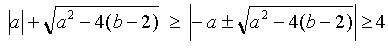
![]()
ยกกำลังสองทั้งสองข้าง
a2 -4(b-2) >= 16 -8|a| +a2
ิb-2 <= 2|a| -4
b+2 <= 2|a| จะได้ว่า |a| >= (b+2)/2
โจทย์ให้หาค่าต่ำสุดของ a2 + b2
a2 + b2 >= [(b+2)/2]2 + b2 = 5b2 /4 + b +1
a2 + b2 >= 5b2 /4 + b +1= (5/4)*[b2 +(4/5)b +4/5)
= (5/4)*[ ( b +(2/5) )2 +4/5-4/25 ]
= (5/4)*[ ( b+(2/5) )2 +16/25 ]
>= (5/4)*[ 0 +16/25 ] = 4/5