เรขาคณิต
(solution
by me)
จะแบ่งการสร้างออกเป็น
2 ขั้นตอนคือ
การสร้างเศษส่วน a/b
และการทำให้เกิด square root
1.
การสร้างส่วนของเส้นตรงยาว
a/b
จะใช้สมบัติของสามเหลี่ยมคล้าย
|
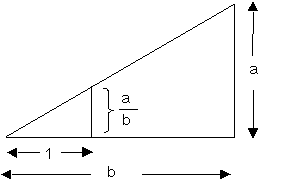
(ใช้สำหรับกรณีที่
b > 1 ซม.) สร้างสามเหลี่ยมมุมฉากรูปใหญ่ที่มีด้านประกอบมุมฉากยาว
a ซม. และ b
ซม.
จากนั้นวัดความยาวจากปลายของด้าน
b ซม. ให้ยาว 1 ซม. โดยใช้ไม้บรรทัด
แล้วลากเส้นตั้งฉากจากจุดนั้นไปยังด้านประกอบมุมฉาก
ด้านดังกล่าวจะยาว a/b ซม. ดังรูป
|
|
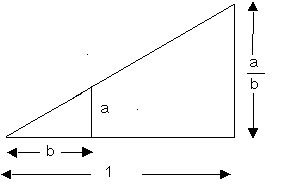
(ใช้สำหรับกรณีที่
b < 1 ซม.) สร้างสามเหลี่ยมมุมฉากรูปใหญ่ที่มีด้านประกอบมุมฉากยาว
a ซม. และ b
ซม.
จากนั้นวัดความยาวจากปลายของด้าน
b ซม. ให้ยาว 1 ซม. โดยใช้ไม้บรรทัดต่อความยาวเส้นออกไปแล้วลากเส้นตั้งฉากจากปลายของเส้น
1 ซม.
ให้ตัดกับเส้นที่ลากต่อจากด้านประกอบมุมฉาก
ด้านดังกล่าวจะยาว a/b ซม. ดังรูป
|
2.
การสร้างส่วนของเส้นตรงความยาว
sqrt(a/b)
จะใช้ทฤษฎีของปีทาโกรัสมาแก้ปัญหา
ซึ่งการสร้างในข้อนี้สามารถสร้างได้หลายรูปแบบ
รูปแบบหนึ่งที่คิดได้คือ
สมมุติว่าให้ด้านตรงข้ามมุมฉากยาว
m+1 และด้านประกอบมุมฉากด้านหนึ่งยาว
abs(m-1)
ด้วยปีทาโกรัสเราสามารถหาความยาวด้านประกอบมุมฉากอีกด้านหนึ่งได้คือ
2*sqrt(m)
ซึ่งหากเราต้องการความยาว
sqrt(m) ก็เพียงใช้วงเวียนแบ่งครึ่งส่วนของเส้นตรงนี้ได้
ดังนั้นหากเราแทนที่
m ด้วยความยาว a/b
ตามที่ได้จากข้อ 1
เราสามารถสร้างความยาว a/b
+1 ได้โดยการลากเส้นต่อจาก
a/b
ให้ได้ความยาว 1
ซม. , สว่น abs(a/b-1)
ก็สร้างในทางกลับกัน
เราก็จะสามารถสร้างส่วนของเส้นตรงความยาว
sqrt(a/b) ได้ในที่สุด
...##

