Actualizada: septiembre, 2005

---

1.- Las funciones serán UNO lógico para:

a) f(A, B, C) = ABC + AB'C'

b) f(A, B, C, D) = AB' + A C' D

2.-El complemento de las funciones dadas es:

a) X'(Y' + Z) + X ( W + V')

b) A' + [B' ( C + D'E)]

c) A' [B' + C (D' + E)]

3.- Mediante manipulaciones algebráicas, empleando teoremas del álgebra booleana, verificar las ecuaciones siguientes:

a) (A + B' + AB) (A + B') A'B = 0
se tiene: (x+y)x = x (absorción); si x = A + B' ; y = AB, entonces:
= (A + B' ) A' B , etc. la intersección de AA' es cero y lo mismo con BB'.
También se puede comprobar por absorción, en el primer paréntesis, que este es igual al segundo.

b) (A + B' + AB') (AB + A'C + BC) = AB + A'B'C

El primer paréntesis por absorción: (A + B')
El segundo por consenso: (AB + A'C)
Por álgebra: AB + AA'C + ABB' + A'B'C , etc

c) (AB + C + D) (C + D') (C + D' + E) = ABD' + C

El segundo y tercer paréntesis se reducen a (C + D') por absorción, igual que en a)
"factorizando" la C
=C + (AB + D) D' , etc.

d) A'B (D' + DC') + (A + DA'C) B = B

= A'B (D' + C' ) + (A + DC) B (absorción), luego B es común a ambos sumandos:
= B (A' D' + A' C' + A + DC)
= B (A' + D'C' + A + DC) ; (A + A) vale uno, entonces todo lo del paréntesis es uno.

4.- COMPLEMENTE las expresiones siguientes:

a) (A + B) (A' + C) + (A' + B + A'BC) (A + A'B) (A' + B)

Simplificando primero,observar que el tercer y quinto paréntesis se reducen a (A' + B) , y el cuarto a (A + B) ; entonces se tiene:
= (A + B) (A' + C) + (A' + B) (A + B) ; Los dos últimos se reducen a B, y los dos primeros mediante la propiedad 12 de los apuntes se modifican:
= AC + A'B + B ; aplicando absorción:
= AC + B
El complemento es (A' + C') B'

b) A'B'C' + A'D + CD + ACD' + A'B + BD' + A'D' + AB

Simplificando, el segundo y séptimo términos se resuelven a: A' ; el quinto y el octavo a B ;se tiene entonces:
= A'B'C' + CD + ACD' + BD' + A' + B ; el primero con el quinto: A' ; el cuarto con el sexto: B, entonces:
= CD + ACD' + A' + B =
= CD + AC + A' + B = ; (segundo con tercero:)
= CD + C + A' + B =
= C + A' + B
El complemento es: A B' C'

5.- Simplifique las expresiones siguientes:

a) A + A'B + (A + B)' C + (A + B + C)' D ... El resultado es A+B+C+D

b) AB' + AC + BCD + D' .....resultado = AB' + BC + D (absorción y consenso)

c) A' + A'B' + BCD' + BD' .. Resultado = A' + BD'

d) AB'C + (B' + C') (B' + D') + (A + C + D)' ... Resultado = B' + C' D'

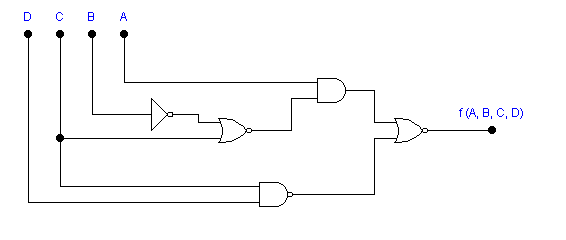
6.- Para el circuito de la figura, escribir la función lógica y simplificar. Resultado: f = CD



7.- La cabina de un aeroplano tiene dos pilotos y un ingeniero. Diseñe un circuito que genere un aviso cuando el ingeniero deje su asiento o cuando ambos pilotos dejen sus puestos.
Resultado: Si se tienen las variables I, Pa y Pb, las cuales serán verdad cuando Ingeniero, Piloto a y Piloto b dejen sus asientos, entonces la función será: f = I + PaPb . Esto se logra con una puerta Y y una O.

8.- Se tienen cuatro variables A0, A1, A2 y A3. Sus valores en un instante cualquiera pueden ser cero o uno lógico. Diseñar un circuito que permita determinar si el número de variables en uno lógico es par o impar. Explicar cómo se pueden usar puertas O-EXClusiva (XOR)
Escribimos la tabla de verdad para una función que sea UNO cuando el número de unos sea impar, se observará que esto se cumple para los números 1, 2, 4, 7, 8, 11, 13 y 14.
Entonces f = A'B'C'D + A'B'CD' + A'BC'D' + A'BCD + AB'C'D' + AB'CD + ABC'D + ABCD' .. y esta función ya no se puede simplificar, requiriéndose 8 puertas AND de 4 entradas y una OR de 8 entradas.
Una solución en este caso es emplear puertas O-EXC (XOR), ya que, para dos variables la función será UNO cuando las entradas sean diferentes (esto implica número de unos impar).
La función anterior es igual a f = A (XOR) B (XOR) C (XOR) D (Una puerta XOR de cuatro entradas).
Como esta función es asociativa, se pueden emplear 3 puertas XOR de dos entradas cada una, es decir:
f = [ [ A (XOR) B ] (XOR) C ] (XOR) D

9.- Para el caso de tres entradas, A, B y C encuentre una expresión lógica para la variable Z, que la haga Z = 1 cuando la mayoría de las entradas sean uno. Simplifique la expresión y dibuje el circuito empleando compuertas Y y O.
Resultado: Z = AB + AC + BC ... (Implica "Uno si dos o más entradas son UNO" )
También: Z = (B + C)(A + C)(A + B) ... ("CERO si dos o más entradas son CERO"). Dibujar ambos circuitos.

10.- Hay tres conmutadores de pared a, b y c. A =1 representa la condición de que el conmutador a está en la posición ARRIBA, y A = 0 representa la posición ABAJO. Análogamente las variables B y C se asocian con los otros dos conmutadores. Suponiendo que los conmutadores puedan emplearse para suministrar entradas a puertas lógicas, diseñe un circuito para que la variable de salida Z pueda ser Z = 1 o Z = 0 manipulando individualmente cada conmutador, independientemente de la posición de los otros.
Resolución: Suponer que inicialmente se tienen los tres conmutadores abajo (000) y que para esta condición la salida es CERO. A partir de esto llenar la tabla de verdad; del enunciado se tiene que cualquier cambio en cualquier conmutador, cambiará la salida.
La función resultante es Z = A'B'C + A'BC' + A B'C' + ABC
Debes encontrar algo familiar en esta expresión. Puedes usar solo dos puertas de dos entradas cada una para realizar la misma función.

11.- Un técnico de laboratorio tiene cuatro productos A, B, C y D , cada uno de los cuales puede encontrarlos en uno cualquiera de dos recipientes de almacenamiento. De vez en cuando es conveniente cambiar uno o más productos de un recipiente al otro. La naturaleza de los productos es tal que es peligroso guardar B y C juntos, a menos que A esté en el mismo recipiente. También es peligroso almacenar C y D juntos a menos que A esté presente. Escribir una expresión lógica para una variable Z, la cual tendrá valor de Z = 1 para cada situación peligrosa de almacenamiento.
La función es: Z = A'B'CD + A'BCD' + A'BCD ; simplificando: Z = A'BC + A'CD

---

UNITEC*-Ing. Jorge Álvarez.


La información vertida en esta página puede y DEBE ser difundida por todo medio posible incluyendo fotocopiado o en archivo electrónico, aunque no le sea dado crédito a la fuente.

URL de esta página: http://members.fortunecity.es/unitec/dd/ddres1.htm
*El nombre UNITEC es propiedad de Universidad Tecnológica de México, S.C.