Gut so. Im Winkelbereich zwischen 0° und 90° entspricht jedem Wert eines Seitenverhältnisses genau ein Winkel.

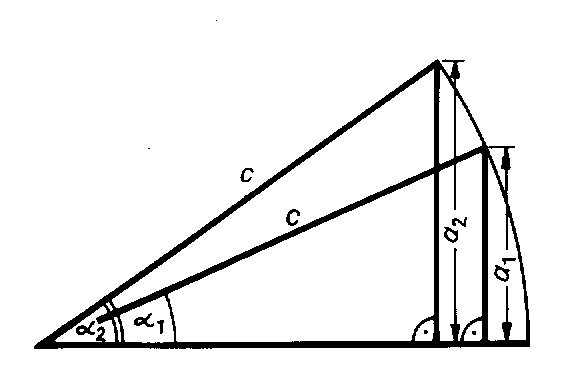
Sehen Sie  sich diese Figur einmal an. Sie enthält zwei rechtwinklige Dreiecke mit der gleichen Hypotenuse c, aber verschiedenen Gegenkatheten  a₁ und a₂. Wie sie sehen, hat das Dreieck mit der größeren Gegenkathete  a₂ auch den größeren Winkel ₂. Es ist also sin ₂ = a₂/c größer als sin ₁ = a₁/c, und umgekehrt gehört zum größeren Wert des Seitenverhältnisses auch der größere Winkel.

Sie können daher Ihren Taschenrechner auch umgekehrt benutzen. Sind zwei Seiten eines rechtwinkligen Dreiecks bekannt, so bilden Sie das Seitenverhältnis und suchen dann mit dem Taschenrechner den Winkel heraus, der zu diesem Seitenverhältnis gehört. Das werden Sie gleich üben. Vorher müssen Sie aber noch eine wichtige Beziehung kennenlernen.

Eine Beziehung zwischen Sinus und Kosinus

Sie erinnern sich, dass die Winkelsumme im Dreieck 180° beträgt; die Summe der spitzen Winkel im rechtwinkligen Dreieck ist daher 90°, sie bilden ein Paar von Komplementwinkeln: + = 90° oder = 90° - .

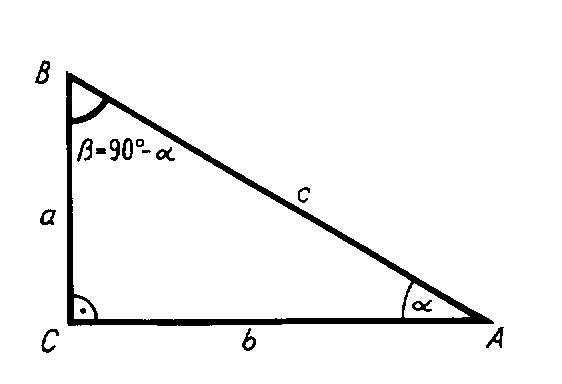
Nun ist sin = a/c. Sehen Sie  sich die Figur einmal aufmerksam an. Mit Hilfe des Winkels = 90° - kann man das Verhältnis noch auf eine andere Weise als Winkelfunktion schrieben.

weiter hier