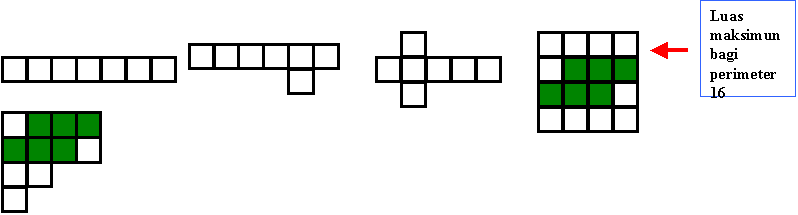
TUGASAN  MATEMATIK BERNAS

Tajuk : Menambah Ubin

Topik Berkaitan : Perkaitan Antara Perimeter Dan Luas 

Tujuan : 

Masalah ini dibentuk untuk menolong pelajar melihat perkaitan di antara luas dan perubahan perimeter.

Rasional :

Dengan mengunakan tugasan matematik yang relevan berdasarkan kaedah inkuiri guru  dan pelajar  boleh menjumpai perhubungan /perkaitan dalam matematik.

Objektif Eksplisit :

1. Pelajar boleh menyatakan perkaitan antara Perimeter dan Luas  sesuatu bentuk objek tertentu.

Aras berkaitan: Tingkatan 1 atau 2 .

Masa : 80 minit

Pengetahuan sedia ada                                       

1. Pelajar tahu mengira dan mengukur perimeter dan luas sesuatu bentuk objek.

2. Pelajar mengetahui konsep poligon.

Pendekatan Pembelajaran : 

Penyiasatan dan Penerokaan Secara Koperatif

Struktur Tugasan :

1.  Pada mulanya aktiviti dijalankan secara individu dan seterusnya secara kumpulan koperatif.

2. Pelajar menyiasat dan meneroka masalah dengan menggunakan kad-kad manila berbentuk segiempat sama(ubin).

3. Pelajar bertanding menjawab soalan-soalan yang diajukan oleh guru dalam kumpulan diskusi.

Bahan-bahan Bantu P&P :

1. Kad-kad manila (Squre 1 cm²)/ubin plastik pelbagai warna.

2. OHP

3. Plastik transparensi

4. Pen transparensi

5. Kertas-kertas "spotty"

Panduan Guru :

Pengenalan

Dalam tugasan ini pelajar-pelajar diberi satu permainan menambah 'ubin'. Ini adalah untuk mengwujudkan satu persekitaran P&P yang menyeronokkan  di kalangan guru dan pelajar-pelajar. Pada mulanya tugasan dijalankan secara individu untuk melihat sejauh mana tahap pemikran yang dipunyai oleh setiap orang pelajar. Mengikut kajian van Hiele terdapat 5 level bagaimana pelajar fikir dan belajar geometri.

• Level 0 : Concrete , pelajar dapat mengenali, menamakan, membanding dan mengoperasi rajah-rajah geometri.

• Level 1 : Analysis, pelajar dapat menganalisa rajah-rajah dan membuat perkaitan antara rajah-rajah melalui pemerhatian.

• Level 2 : Informal Deduction, pelajar menjumpai dan mengeneralisasi formula berdasarkan ciri-ciri awal yang dipelajari dan membangunkan hujah informal  untuk menunjukkkan generalisasi itu benar.

• Level 3 : deduction, pelajar dapat buktikan teorem deduktif  dan faham struktur sistem geometri.

• Level 4 : Rigor, pelajar mengukuhkan teorem mengikut sistem postulasi yang berbeza dan membanding serta menganalisa sistem itu.

Bagaimana guru boleh menolong membangunkan pemikiran pemikiran pelajar:

• membantu pelajar kumpul maklumat dan membuat tugasan dengan melihat contoh-contoh.

• menggalakkan pelajar menyempurnakan tugasan ini ('Tambah Ubin") kepada rajah sebagai satu cabaran. Minta pelajar buat ringkasan atau refleksi tentaang apa yang dipelajari.

• Bahasa Komunikasi yang bermotivasi dan menarik oleh guru dapat memajukan pelajar dari pemikiran secara konkrit---> visual---->abstrak.

• mengadakan kumpulan diskusi supaya pelajar-pelajar dapat berkongsi  bersama idea-idea yang bernas.

Oleh sebab itu, objektif pembelajaran ini tidak akan tercapai melainkan :

• guru benar-benar memahami kajian van Hiele dalam meningkatkan kefahaman geometri.

• guru menyediakan tugasan-tugasan yang kaya dan bernas kepada pelajar bukan hanya setakat mengukur perimeter dan luas sahaja.

• menggalakan interaksi sosial antara pelajar-pelajar agar mereka dapat menggunakan bahasa sebagai alat untuk memajukan diri masing-masing.

1.  Pelajar-pelajar di dalam kelas dibahagikan kepada kumpulan mengikut pelbagai kebolehan.(Disyorkan 4 orang sekumpulan supaya semua pelajar boleh berinteraksi secara aktif).

2. Kertas-kertas "spotty" diedarkan sebagai Set Induksi guru. Soalan dari guru- Adakah kaitan bentuk-bentuk yang dilukis oleh pelajar  dengan poligon? Guru meminta pelajar memberi takrifan poligon.

3. Kad-kad manila 'Squares' dan lembaran kerja diedarkan kepada pelajar.

4. Semasa pelajar-pelajar menjalankan tugasan mereka, pemantauan dan bimbingan dari guru diberikan. Masalah yang mungkin wujud "Lupa Apa Itu Poligon". Contoh-contoh soalan yang dapat mencetus minda pelajar dan seterusnya mengukuhkan konsep poligon yang sedia ada ialah:  - Apakah yang dimaksudkan dengan poligon? Bagaimanakah untuk mengira perimeter poligon yang dibentuk itu?

5. Guru hendaklah membimbing dan memberi pengukuhan positif kepada pelajar sekiranya mereka memberi jawapan yang salah.

6. Selepas proses pembinaan konsep mengenalpasti perimeter poligon dijalankan oleh pelajar, guru akan menerangkan dengan jelas konsep tersebut dengan bantuan transparensi OHP

7. Untuk mengetahui sejauh mana objektif pelajaran tercapai guru akan menjalankan pentaksiran di akhir pengajaran.(Oral/Bertulis)

Guru boleh merujuk kepada lampiran ini untuk sesi penerangan dan perbincangan 

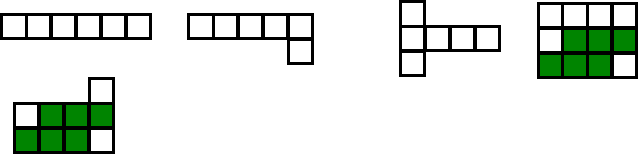
Perimeter	Bentuk-bentuk rajah selepas penambahan ubin yang mungkin dilukis oleh pelajar
12
13
14
15
16

Tugasan Pelajar:

1. Aktiviti secara individu: -bertujuan menyiasat pelajar faham tentang bentuk-bentuk dan dapat mengaitkannya dengan poligon.

- (Set Induksi)Pelajar diminta menyambung titik-titik  dengan lengkap secara bebas di kertas "spotty".

-Pelajar diminta menyatakan takrifan poligon.

-Pelajar diminta melukis sendiri rajah-rajah yang mempunyai perimeter 8 hingga 12.(Peruntukkan masa 20 minit)

2. Aktiviti secara kumpulan:

-Pelajar diminta membentuk rajah-rajah yang mempunyai perimeter yang telah ditetapkan dan melukisnya di dalam jadual berikut : 

Guiding Questions for Group Discussion

1.Where would you place a tile to increase the perimeter by 1? By 2? By 3?

2. How could you increase the area by 3 and not increase the perimeter?

3. What is the fewest number of tiles that can be added to increase the perimeter to 16 units? Describe this new shape. What is its area?

4.  What is the greatest number of tiles that can be added to increase the perimeter to 16 units? Describe this new shape. What is its area?

5.  Use the tiles to find all the noncongruent rectangles that have a fixed integral perimeter. Perimeters could vary from 12 to 24 units. 

     (Note: Could a perimeter be an odd number?)

[Balik Ke Menu Tugasan Bernas Matematik]