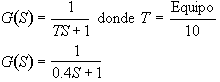
Desarrollo
La práctica consiste de las siguientes partes:
a.1) Obtener a partir de la función de transferencia de un sistema de primer orden la respuesta en tiempo a: Impulso, Escalón y Rampa.
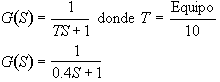
+ Graficar la posición de las raíces.
![]()
Dividiendo entre t para normalizar:
![]()
Como es una funcion de 1er Orden solo tiene un polo y un cero , el cero se encuentra en ¥ , obteniendo el polo tendriamos:
![]()
![]()
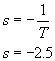
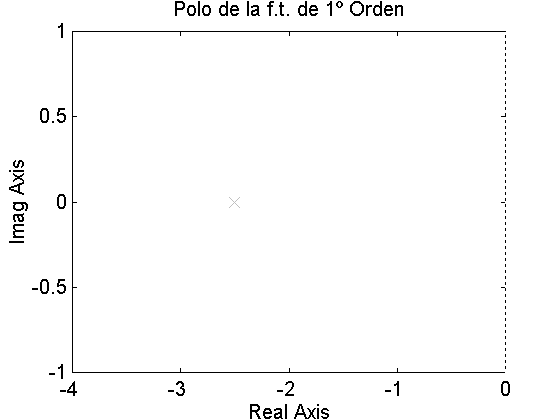
Usando el comando pzmap de MatLab encontramos su único polo en -2.5 (1/T), este polo nos indica el tiempo de estabilización del sistema (Tsc=5T=2 segundos).
Impulso
d(t).+ Obtener matemáticamente la ecuación de la respuesta.
![]()
Excitando la funcion impulso en la Funcion de Transferencia quedaria:![]()
![]()
Dividiendo entre T:
![]()
Antitransformando quedaria:
![]()
esto implica que:
![]()
Como:
![]()
Por lo tanto:![]()
![]()
Substituyendo:
![]()
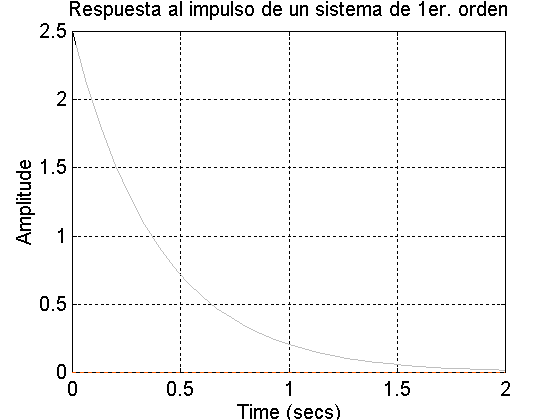
Respuesta al impulso de un sistema de primer orden.
+ Escribir las instrucciones para obtener la respuesta en MATLAB.
Las instrucciones para obtener la respuesta en MatLab son:
num=[1];
den=[0.4 1];
impulse(num,den);
title(‘Respuesta al impulso de un sistema de 1er. orden’);
grid;
Escalón unitario u(t).
+ Obtener matemáticamente la ecuación de la respuesta.
Como primer punto hay que transformar a el plano de Laplace la funcion escalon m (t).
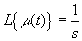
excitando el sistema con un escalon quedaria:
![]()
Normalizando:
![]()
Dividiendo entre T y substituyendo T.
![]()
Aplicando fracciones parciales:
![]()
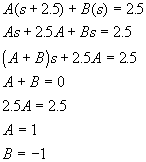
La ecuacion quedaria como sigue:
![]()
Haciendo la tranformada inversa quedaria:
![]()
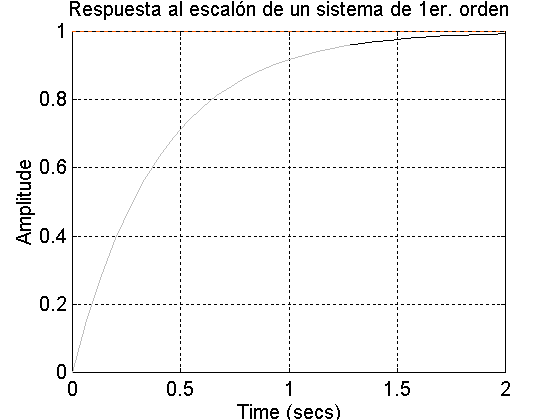
+ Escribir las instrucciones para obtener la respuesta en MATLAB.
num=[1]
den=[0.4 1]
step(num,den);
title(‘Respuesta al escalón de un sistema de 1er. orden’);
grid;
Rampa unitaria r(t).
+ Obtener matemáticamente la ecuación de la respuesta.
La transformada de Laplace de una funcion F(t)=t es:
![]()
Excitando el sistema de 1er Orden con una funcion rampa quedaria:
![]()
Dividiendo entre T y sustituyendo quedaria:
![]()
Aplicando fracciones parciales quedaria:
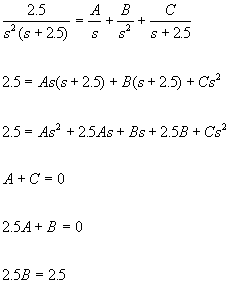
Por lo tanto A=-.4, B=1, C=.4
La funcion quedaria:
![]()
Antitransformando:
![]()
+ Escribir las instrucciones para obtener la respuesta en MATLAB.
num=[1]
den=[0.4 1]
t=linspace(0,2,100);
u=t;
lsim=(num,den,u,t);
title(‘Respuesta a la rampa de un sistema de 1er. orden’);
grid;
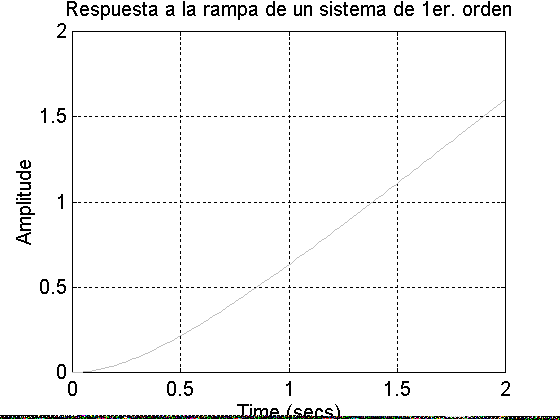
+Concluir sobre la relación entre la posición de los polos y la respuesta obtenida:
El polo se encuentra en -2.5, y el tiempo de estabilización de la respuesta esde 2 segundos. Estos dos datos se relacionan de la siguiente forma:
1/T=1/0.4=2.5
5T=5*0.4=2 seg
Es decir, la distancia del polo al origen es inversamente proporcional al tiempo de establecimiento del sistema.