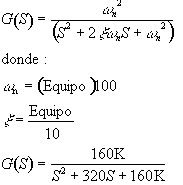
a.2) Obtener la respuesta a escalón unitario u(t) a partir de la función de transferencia de un sistema de segundo orden, caso subamortiguado

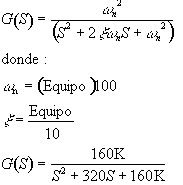
+ Graficar la posición de las raíces.

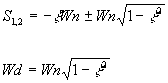
Substituyendo para encontrar los polos de la ecuacion:

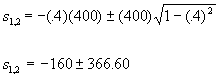
El sistema tiene 2 raices en ¥ . Usando pzmap de MatLab encontramos los polos de esta f.t. en -160± 366.6j, la parte real es xWn y es inversamente proporcional al tiempo de duración del transitorio, la parte imaginaria es Wd y es igual a la frecuencia del transitorio.

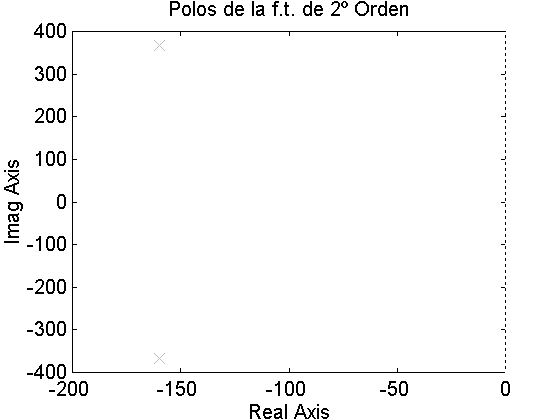
+ Obtener matemáticamente la ecuación de la respuesta.

Substituyendo en la ecuacion

Aplicando Fracciones parciales quedaria:

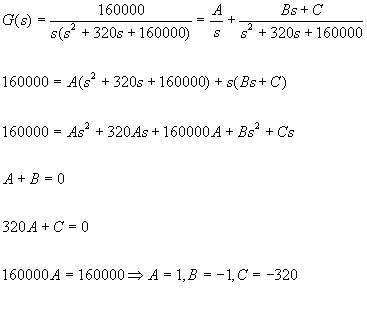
Substituyendo las constantes quedaria:

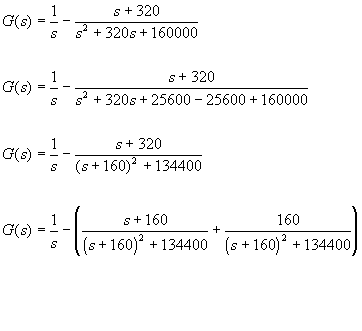
Antitransformando:

Asi nos quedaria que:

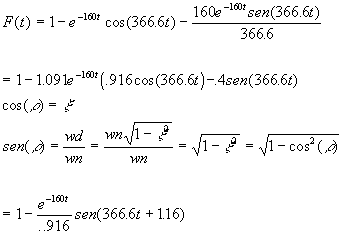
+ Escribir las instrucciones para obtener la respuesta en MATLAB.

num=[160e3];

den=[1 320 160e3];

step(num,den);

title(‘Respuesta al escalón de un sistema de 2o. orden’);

grid;

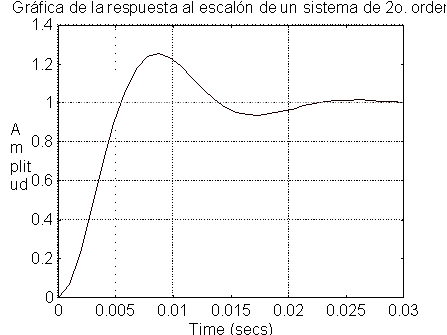
+Concluir sobre la relación entre la posición de los polos y la respuesta obtenida.

Vemos claramente que el par de polos complejos graficados, producen una frecuencia natural de valor Wd que se ve en la parte cosenoidal de la función en el tiempo, la parte real del polo se aprecia como el tiempo de establecimiento exponencial de dicha función.