Respuesta en tiempo de sistemas Físicos

1.- Introducir el concepto de CACSD(Computer Aided Control Systems Design).

2.- Introducir el concepto de Función de Transferencia.

3.- Analizar la respuesta en tiempo de sistemas de:

+ Primer Orden

+ Segundo Orden

- Caso Subamortiguado

- Caso Críticamente amortiguado

- Caso Sobreamortiguado

- Caso oscilatorio

+ Orden Superior

- Polos Dominantes

- Efecto de los Ceros

4.- Analizar la relación entre los polos del sistema y la respuesta transitoria del mismo.

1.- Respuesta dinámica de sistemas físicos.

Existen dos tipos de sistemas físicos: los sistemas estáticos y los sistemas dinámicos. Los sistemas estáticos son aquellos cuyos elementos no almacenan energía, su respuesta se caracteriza por no tener transitorio. En contraposición los sistemas dinámicos son aquellos cuyo elementos almacenan energía (o al menos uno de ellos), por lo que su respuesta contiene un transitorio; todos los sistemas reales son dinámicos.

1.1.- Respuesta transitoria y respuesta en estado estable.

La respuesta dinámica de los sistemas físicos está formada por dos componentes: respuesta transitoria y respuesta en estado estable. La respuesta transitoria es la forma en la que responde un sistema al pasar de un estado inicial a uno final. La respuesta en estado estable es la forma como responde un sistema cuando el tiempo tiende a infinito.

1.2.- Error en estado estable.

Cuando la salida de un sistema no iguala a la entrada (en t=¥ ), se dice que tiene un error en estado estable.

2.- Función de transferencia

2.1.- Definición

Se define como función de transferencia de un sistema lineal invariante en el tiempo a la razón entre la transformada de Laplace de la salida y la transformada de Laplace de la entrada tomadas con condiciones iniciales cero.

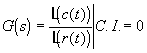
Características de la f.t. :

1) Es la forma típica de modelos en control clásico.

2) Es un modelo que relaciona la salida de un sistema SISO con la entrada en términos de los parámetros del mismo.

3) Es una característica propia del sistema y no depende de la entrada, ni de ninguna otra variable intermedia.

4) Muy comúnmente la f.t. es válida en un rango de operación.

5) La f.t. no proporciona información sobre la naturaleza del sistema, así existen los llamados sistemas análogos cuya f.t. es idéntica.

3.- Respuesta en tiempo en función de la posición de los polos del sistema

Polos: Son aquellos valores de s que hacen que la f.t. tienda a ¥ .

Ceros: Son aquellos valores de s que hacen que la f.t. tienda a 0-

Cualquier f.t. siempre tiene el mismo número de polos que de ceros.

La respuesta transitoria de un sistema dinámico es función del tipo de polos de su f.t.. Los ceros de la f.t. afectan la amplitud relativa de las diferentes componentes de transitorio; sin embargo no afectan el tipo de transitorio.

3.1.- Sistemas de Primer Orden

Un sistema de primer orden generalizado tiene como f.t.:

donde T es la constante de tiempo del sistema.

Si a un sistema como este (de primer orden) se le excita con un impulso se obtendría la respuesta:

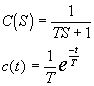
La respuesta a un escalón sería:

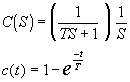
La respuesta a una rampa sería:

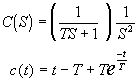
En las tres respuestas anteriores se define como tiempo de establecimiento Tsc a la duración del transitorio de la respuesta dinámica del sistema, este Tsc es cinco veces T. Por otra parte al graficar el polo de la f.t. de un sistema como este lo encontraremos en -1/T sobre el eje real. Por todo esto se puede decir que: El tiempo de establecimiento Tsc es inversamente proporcional a la distancia entre el origen y la magnitud del polo del sistema.

3.2.- Sistemas de Segundo Orden

Un sistema generalizado de segundo orden tiene la siguiente f.t.:

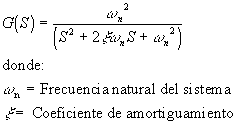
La respuesta transitoria del sistema depende del tipo de raíces del denominador de esta f.t. (polos):

Con lo que se pueden dar cuatro tipos de sistemas:

1) Subamortiguado 0<x <1 genera raíces complejas conjugadas

2) Críticamente amortiguado x =1 genera raíces reales iguales y negativas

3) Sobreamortiguado x >1 genera raíces reales dif. y negativas

4) Oscilatorio x =1 genera raices imaginarias

+ Rectas de x=cte, círculos de Wn=cte.

Al graficar estas raíces (polos de la f.t. de 2° orden) en el plano complejo podemos definir rectas de x=cte y círculos de Wn=cte. Las rectas de x nos definen el ángulo de elevación del polo: cos(f)= -x. Mientras que Wn nos da la distancia del origen al polo.

3.3.- Efectos de los ceros en la respuesta dinámica.

Los ceros afecta la forma de la respuesta de la f.t. minimizando a los polos que se encuentran en su vecindad.

3.4.- Sistemas de orden Superior

Los sistemas de orden superior son aquellos en donde el orden del denominador de su f.t. es mayor que dos. El tipo de respuesta transitoria depende del tipo de raíces del denominador, mientras que la forma relativa del transitorio se ve afectada por los ceros de la f.t.

La respuesta transitoria de un sistema de orden superior es una suma de los transitorios asociados a cada uno de los residuos de las funciones parciales; Es decir a cada una de las respuestas de las raíces del sistema, las cuales pueden ser de 1° o 2° orden.

+ Polos dominantes

Se dice que la respuesta de un sistema de orden superior está dominada por un par de polos complejos conjugados cuando:

1) Todos los demás polos están lejos a la izquierda (al menos seis veces más lejos del origen).

2) Aquellos polos que no estén lejos a la izquierda deben tener un cero cercano.

Si un sistema de orden superior tiene polos dominantes es correcto hacer un análisis exclusivo de la f.t. que genera dichos polos y omitir los otros términos.