Universidad Iberoamericana

Práctica 2:

Simulación de Sistemas Dinámicos por CACSD

Profesor Sergio Montúfar.

Carral Robles-León, Sandra.

Iniestra , Víctor.

Morrill Valiente, Fernando.

Práctica 2.

Simulación de Sistemas Dinámicos por CACSD.

Objetivos:

-Introducir el concepto de simulación de sistemas dinámicos asistida por computadora.

-Obtener modelos matemáticos de sistemas físicos utilizando redes de impedancias y analizar su respuesta dinámica usando CACSD.

-Introducir el concepto de Diagramas de Bloques.

-Obtener diagramas a bloques de sistemas físicos y representarlos en un simulador basado en computadora.

-Obtener la respuesta dinámica de un sistema a partir de su Diagrama a Bloques utilizando CACSD.

-Conocer las herramientas de simulación disponibles en MATLAB a través del modulo SIMULINK: Dinamic System Simulation Software.

Conceptos Teóricos:

1. Diagramas de Bloques:

a) Definición. Son una representación gráfica de un conjunto de ecuaciones algebraicas simultáneas que normalmente corresponden a un conjunto de ecuaciones diferenciales transformadas a Laplace.

Se utilizan para simplificar el análisis de los sistemas lineales invariantes en el tiempo.

También permiten Identificar la función de cada uno de los elementos del sistema, así como la interpelación entre cada uno de ellos.

b) Construcción a partir de las ecuaciones dinámicas. En términos generales el diagrama a Bloques de un sistema lineal invariante en el tiempo se puede obtener siguiendo estos pasos:

1) Obtener las ecuaciones dinámicas del sistema y transformarlas a Laplace con condiciones iniciales 0.

2) Despejar cada variable del sistema en términos de las entradas de las demás variables y de los parámetros del sistema.

3) Representar a cada ecuación del inciso anterior mediante un conjunto de Bloques.

4) Ensamblar todos los subconjuntos en un solo diagrama a bloques total utilizando puntos suma y puntos de bifurcación.

c) Características.

1) Cualquier sistema lineal invariante en el tiempo puede ser representado mediante un diagrama a bloques.

2) Puede haber distintos diagramas a bloques para un mismo sistema dependiendo de el punto de análisis deseado.

3) Nos da información sobre el comportamiento dinámico del sistema pero no sobre su naturaleza.

4) Es posible tener diagramas a bloques iguales para sistemas de distinta naturaleza (Sistemas Análogos).

2. Funciones de Álgebra de bloques en Control systems toolbox de MATLAB (series, parallel, Feedback).

SERIES Conexión en serie de dos sistemas.

u --->[Sistema1]--->[Sistema2]----> y

[NUM,DEN] = SERIES(NUM1,DEN1,NUM2,DEN2) produce el SISO (system input, system output) de la función de transferencia de 2 sistemas, al conectarlos en serie.

PARALLEL Conexión en paralelo de dos sistemas.

+-->[Sistema1]--+

u-->+ O--->y

+-->[Sistema2]--+

[NUM,DEN] = PARALLEL(NUM1,DEN1,NUM2,DEN2) produce una conexión en paralelo de las funciones de transferencia de dos sistemas.

FEEDBACK Conexión de retroalimentación de dos sistemas.

u-->O-->[Sistema1]---+--->y

| |

+---[Sistema2]<--+

[NUM,DEN] = FEEDBACK(NUM1,DEN1,NUM2,DEN2,SIGN) produce la respuesta de la conexión en retroalimentación de dos funciones de transferencia, con el signo SIGN.

3.- Construcción de modelos ( Diagramas a Bloques ) en Simulink: ‘sources, sinks & conections libraries’.

Entramos a SIMULINK desde MATLAB. Una vez en SIMULINK, creamos un archivo nuevo con extensión m. Para poner el step input, nos vamos al cuadro que dice Sources en la ventana de SIMULINK, y le damos doble click. Arrastramos el cuadro de Step Input a la ventana del archivo nuevo.

Para la función de transferencia, nos vamos a Linear, y repetimos el procedimiento anterior.

El graficador auto-escala se encuentra en el bloque de Sinks.

Se conectan los bloques entre sí.

Para editar los valores del Step input y de la(s) Función(es) de Transferencia, se da doble click sobre el ícono correspondiente.

Posteriormente, se editan los parámetros de la simulación en el menú Simulation, Parameters..., poniendo el tiempo inicial y final, y los tiempos de paso deseados.

Para comenzar la simulación, se activa en el menú Simulation, Start.

4.- Simulación de modelos de Simulink desde Matlab: Algoritmos de integración numérica y variables de regreso.

Para poder ejecutar simulaciones de diagramas de bloques de SIMULINK desde MATLAB, se necesita que el diagrama del SIMULINK tenga un inport a la entrada, y un outport a la salida, los cuales se encuentran en Conections. Desde MATLAB ejecutamos el comando linsim, cuyos parámetros son los siguientes:

Nombre del archivo donde se encuentra el sistema de SIMULINK.

Tiempo final de la simulación.

Condiciones iniciales en forma de matriz.

Una matriz en las que se puede definir:

El error relativo de linsim.

Los tiempos de paso mínimos y máximos deseados.

Activar el despliegue de advertencias al término de la ejecución.

El parámetro de plot.

NOTA: Si esta matriz queda vacía, entran las condiciones de default.

La entrada del sistema en forma matricial de dos columnas, o en forma de función predefinida.

Desarrollo:

La practica consta de las siguientes partes :

1) Para el siguiente sistema mecánico traslacional :

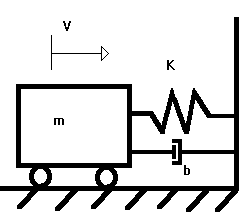
Los valores de m1, K1, b1, m2, K2, b2 son diferentes para cada equipo:

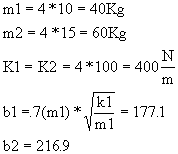
Encontrar:

a) Red de Impedancias del sistema.

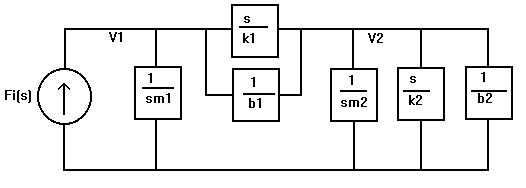
b) Ecuaciones Dinámicas.

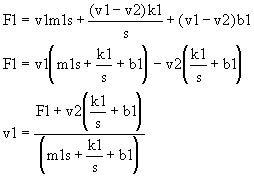
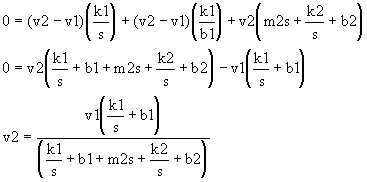
c) Diagramas a Bloques.

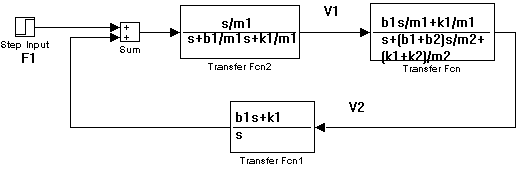
d) Construir el diagrama a bloques en Simulink.

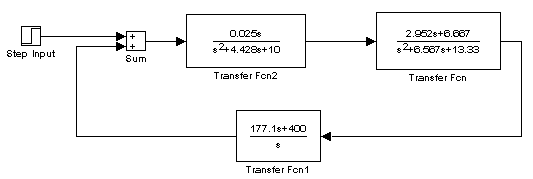
e) Funciones de transferencia ( utilizar MATLAB ).

y

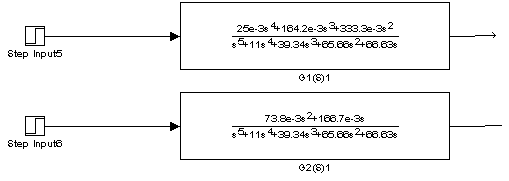
f) Graficar la respuesta a escalón de las 2 salidas (V1 y V2) a partir de las funciones de transferencia obtenidas utilizando funciones de Matlab.

Gráfica de la respuesta de V₁ usando comandos MATLAB

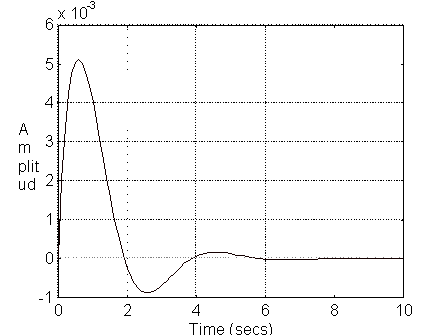
Gráfica de la respuesta V₂ usando comandos de MATLAB

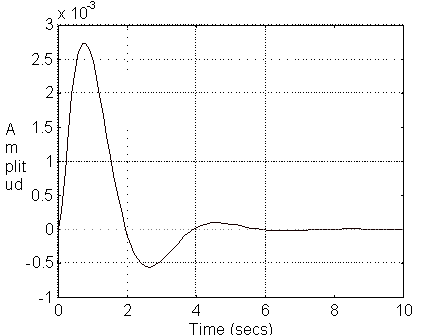
Los comandos que se utilizaron para obtener las gráficas anteriores fueron:

den1=[1 4.428 10];

num2=[2.952 6.667];

den2=[1 6.567 13.33];

num3=[177.1 400];

den3=[1 0];

t=linspace(0,10);

[num4,den4]=series(num1,den1,num2,den2);

[num5,den5]=feedback(num4,den4,num3,den3,1);

step(num5,den5,t);

g) A partir del diagrama a bloques de Simulink, simular las 2 salidas del sistema (V1 y V2) para un escalón de magnitud unitaria en la fuerza Fi utilizando Simulink de Matlab. Utilizar dos osciloscopios o graficadores uno para cada salida, cada uno con 2 trazos, uno para la entrada y otro para la salida correspondiente.

Gráfica de las respuestas de V₁ y de V₂ usando SIMULINK

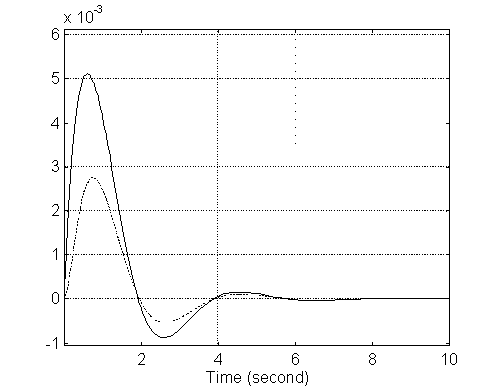
NOTA: No se graficó cada respuesta contra su respectiva entrada, puesto que, como la entrada es un escalón de magnitud unitaria, no se apreciaría totalmente la salida, pues la escala de ésta es muy pequeña.

h) Comparar los resultados de los 2 incisos anteriores y concluir sobre las diferencias si existen.

No hay ninguna diferencia entre las gráficas anteriores, por lo cual podemos concluir que por cualquiera de los dos métodos, se llega a un mismo resultado.

2) Para el siguiente sistema Hidráulico:

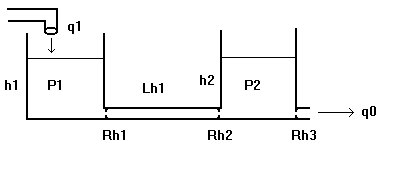
Los valores de Ch1, Rh1, Lh1, Ch2, Rh2 y Rh3 son :

a) Red de impedancias del sistema.

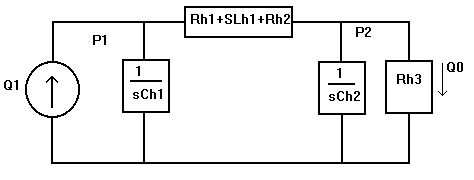
b) Ecuaciones Dinámicas del sistema.

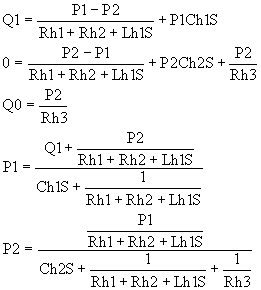
c) Diagrama a bloques.

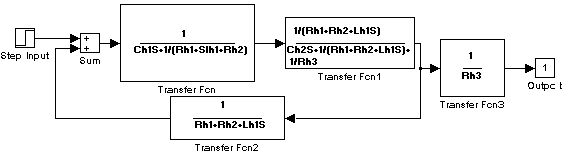
d) Construir subsistemas en SIMULINK formados por 2 o más bloques para simplificar el diagrama obtenido.

p2hid:

p2hid1:

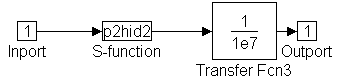
p2hid2:

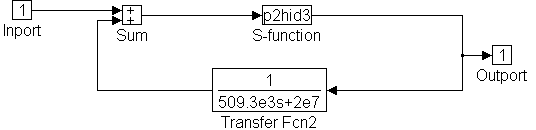
p2hid3:

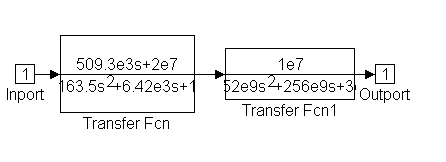
e) Construir el diagrama a bloques total simplificado en SIMULINK utilizando estos subsistemas así como variables de regreso a MATLAB.

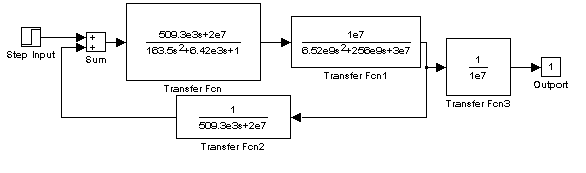
f) Simular el sistema desde MATLAB y capturar las variables de regreso. Graficar la entrada y la salida del sistema mediante las funciones de graficación tradicionales de MATLAB (Plot). Utilizar una sola gráfica con Titulo y ejes coordenados con nombre.

Gráfica de la respuesta del sistema hidráulico al escalón utilizando comandos de MATLAB

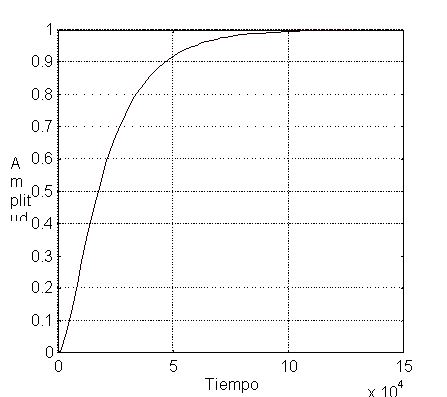
Los comandos que se utilizaron para obtener las gráficas anteriores fueron:

» t=linspace(0,13000);

» t=t';

» for i=1:1.3e3:130000

u=[u,1];

end

» u=u';

» ut=[t,u];

»[x,y]=linsim('p2hid',130000,[],[],ut);

»plot(x,y);

» grid

» title('');

» ylabel('Amplitud');

» xlabel('Tiempo');

Conclusiones Finales:

La simulación por computadora constituye una herramienta muy útil para el diseño y fabricación de sistemas de control, pues no es necesario armar y probar un sistema para saber que funciona, lo cual requeriría de un costo elevado.

Fue bueno hacer simulaciones de sistemas de SIMULINK desde MATLAB, ya que de esta forma, podemos definir funciones de entrada de cualquier tipo.

Es importante que utilicemos las herramientas de trabajo de SIMULINK, pues es una herramienta poderosa dentro de MATLAB; y al conocerlo, podemos aprovechar al máximo el software para la simulación.

Por otro lado, la utilización de diagramas a bloques para obtener la función de transferencia, y con la ayuda de MATLAB, hace más simple y directo el manejo del sistema, así como su respuesta a distintas entradas.

Índice.

Simulación de Sistemas Dinámicos por CACSD.

Presentación.

Índice.

Objetivos.

Conceptos teóricos.

Diagramas a bloques:

a) Definición.

b) Construcción a partir de ecuaciones dinámicas.

c) Características.

Desarrollo.

Sistema 1:

a) Red de impedancias.

d) Diagrama en SIMULINK.

e) Funciones de transferencia en MATLAB.

f) Gráficas.

g) Simulación en SIMULINK.

h) Conclusiones.

Sistema 2:

a) Red de impedancias.

b) Ecuaciones dinámicas.

c) Diagrama a bloques.

d) Subsistemas en SIMULINK.

e) Diagrama en SIMULINK.

f) Simulación en MATLAB.

Conclusiones finales.