Objetivos Generales:
1. Diseñar y construir un servoposicionador formado por tres partes:
C Sistema mecánico (motor de D.C. + masa-resorte-amortiguador).
C Actuador de potencia basado en transistores.
C Sistema de control electrónico basado en OPAMPíS.
2. Obtener el modelo matemático del servoposicionador utilizando redes de impedancias y diagramas de bloques.
3. Obtener los parámetros del modelo matemátio del sistema a partir de datos experimentales.
4. Introducir el concepto de control proporcional y analizar la respuesta del sistema para distintos valores de ganancia de lazo abierto (Kol, utilizando como herramienta el método de root locus.
5. Simular la respuesta dinámica del servoposicionador a partir de su diagrama a bloques utilizando MATLAB y SIMULINK (CACSD).
6. Comparar la resuesta dinámica real con la del simulador (CACSD), y concluir sobre las diferencias y sus posibles causas.
7. Analizar los cambios en la respuesta dinámica del sistema ante variaciones en los parámetros, utilizando el método de root locus en MATLAB (CACSD).
Objetivos Específicos:
8. Practicar el uso de OPAMPíS para la implementación de sistemas de control analógicos.
9. Practicar el uso de transistores para la implementación de actuadores de potencia.
10. Identificar los problemas existentes en la construcción de un sistema mecánico elemental.
11. Identificar los problemas y limitaciones existentes en un sistema electrónico para controlar una planta mecánica.
Desarrollo:
1. Sistemas retroalimentados: Aplicación de conceptos teóricos a sistemas de control reales:
C Error en estado estable y constantes de error.
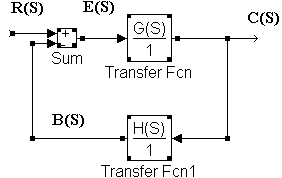
Constantes de Error à Sea el siguiente sistema generalizado:

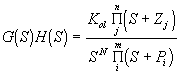
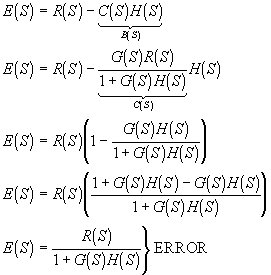
Así, el error en un sistema de control depende tanto de la naturaleza del mismo (función de transferenia ), como de la entrada a la que se ha sometido.
El error en estado estable puede obtenerse a partir de la ecuación anterior, utilizando el teorema del valor final:
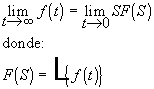
y así, el error en estado estable es:
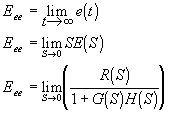
Error en Estado Estable para Entrada Escalón à
![]()
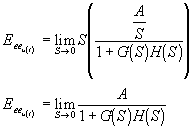
Se define K0=constante de error a escalón (posición), como:
![]()
Para sistemas de tipo N=0,
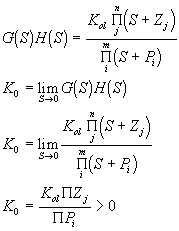
y así:
![]()
Para sistemas de tipo N³ 1,
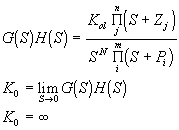
Así:
![]()
Error en Estado Estable para Entrada Rampa à
![]()
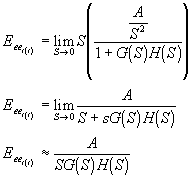
Se define K1=constante de error a rampa (velocidad), como:
![]()
Para sistemas de tipo N=0,
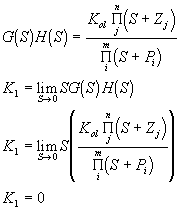
y así:
![]()
Para sistemas de tipo N=1,

Así:
![]()
Para sistemas de tipo N³ 2,
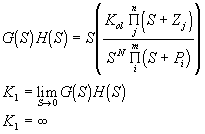
Así:
![]()
C Método del lugar de las raíces (root locus).
Las características de la respuesta transitoria de un sistema, dependen del tipo de raíces del denominador de la función de transferencia de lazo cerrado del sistema.
Para un sistema retroalimentado generalizado:
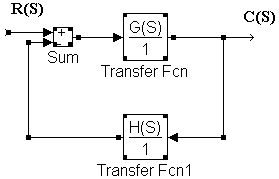
la función de transferencia de lazo cerrado será:

Al denominador se la función de transferencia de lazo cerrado se le llama "ecuación característica" del sistema.
Así, la ecuación característica de un sistema general tendrá la forma:
![]()
Si el sistema es de orden "n", esta ecuación será de orden "n", y sus raíces serán los polos del sistema.
En los años 50ís, W.R. Evans desarrolló un método matemático mediante el cual es posible graficar el valor de las raíces de lazo cerrado (polos del sistema) al variar un parámetro del sistema desde cero hasta ¥ .
Actualmente, este parámetro variable es la ganancia de lazo abierto (Kol) del sistema de control.
C Análisis del efecto de la ganancia de lazo abierto (Kol) sobre la respuesta dinámica de un sistema de control.
La respuesta transitoria de un sistema depende de las raíces de su ecuación característica (polos del sistema), la cual se modifica al variar Kol.
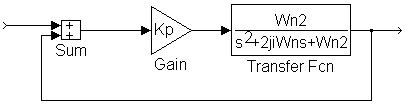
2. Sistema de control proporcional.
C Definición.
Este controlador amplifica la señal de error Kp veces para generar la señal de mando como
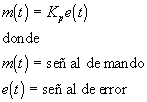
En Laplace,
![]()
La función de transferencia de lazo abierto es:
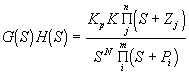
y entonces, Kol=KKp.
C Análisis del efecto de la ganancia proporcional (Kp) sobre la respuesta dinámica de un sistema de control.
El análisis de la respuesta dinámica de un sistema con control proporcional es análogo a analizar el root locus de dicho sistema.
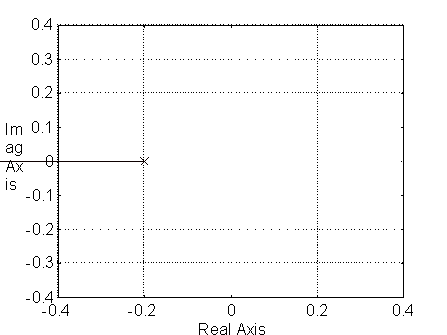
C Análisis de sistemas de primer orden con control proporcional.
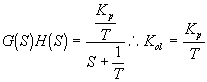
El root locus para T=5 queda:
C Análisis de sistemas de segundo orden con control proporcional.
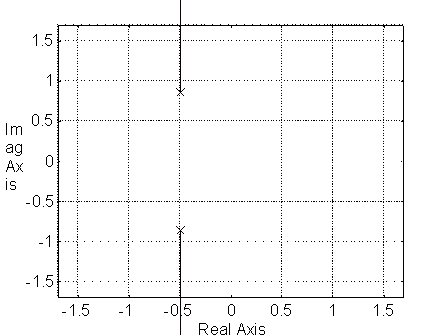
C Caso subamortiguado.
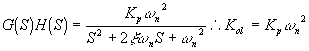
El root locus para w n=x =1 queda:
C Caso críticamente amortiguado.

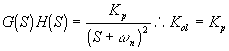
El root locus para w n=2 y x =Ĺ queda:
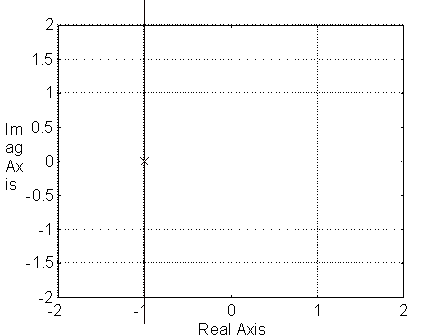
C Caso sobreamortiguado.

![]()
El root locus para w n=1.414 y x =1.061 queda:
3. Sistema de control electrónico.
C Ventajas y desventajas.
Es más económico un sistema mecánico, pero también es más difícil de calibrar. Sin embargo, un sistema electrónico es más confiable, ya que los componentes duran más, hay menos desgaste, y es más fácil de monitorear a grandes distancias.
C Implementación por medio de OPAMPíS.
Se utilizan OPAMPíS en el detector de error, en la amplificación Kp, en el integrador y en el derivador.
C Actuador de potencia basado en transistores.
La parte de potencia se controla mediante transistores, que a su vez son controlados mediante un OPAMP en configuración de buffer. El voltaje máximo que puede salir de este arreglo está limitado por la polarización del OPAMP. Sin embargo, la corriente que se demanda sale de la polarización de los transistores.
Desarrollo:
La práctica consta de las siguientes partes:
1. Construcción de la planta mecánica.
Construir el siguiente sistema mecánico:
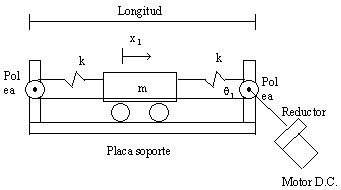
Los valores de m1, k1 y b1 dependen de la implementación mecánica del servoposicionador, sin embargo, deben estar dentro de los siguinetes rangos:
C m=300-600 g.
C k=1/10 Kg/cm.
C Long.= 70-100 cm.
2. Obtención del modelo matemático:
Para el sistema mecánico construido, encontrar:
a) Red de impedancias de la planta.
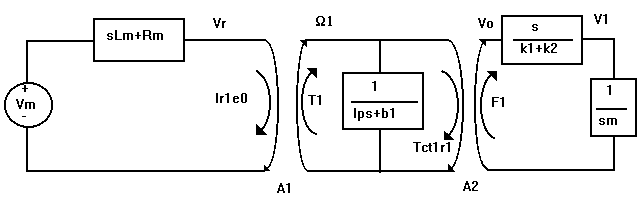
b) Ecuaciones dinámicas.
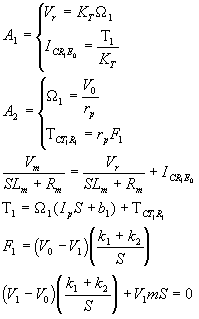
c) Diagrama a bloques.
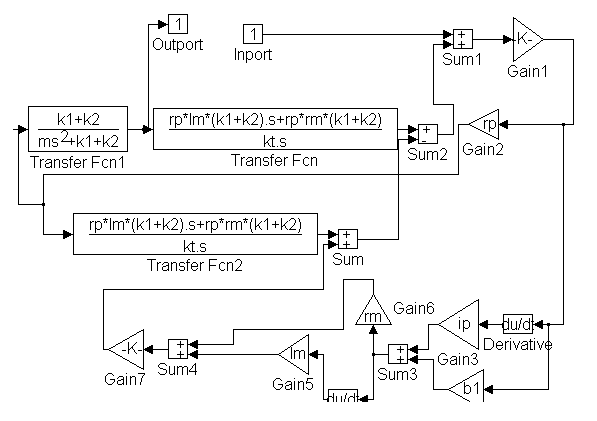
d) Funciones de transferencia:
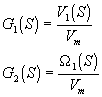
![]()

gan=kt * (k1 + k2) * rp /(ip * lm * m)
ters4=ip * lm * m
ters3=(b1 * lm * m + ip * m * rm) / ters4
ters2=(ip * k1 * lm + ip * k2 * lm + kt^2 * m + b1 * m * rm + k1 * lm * m * rp^2 + k2 * lm * rm * rp^2)/ters4
ters1=(b1 * k1 * lm + b1 * k2 * lm + ip * k1 * rm + ip * k2 * rm + k1 * m * rm * rp^2 + k2 * m * rm * rp^2 )/ters4
ters0=(kt^2 * k1 + kt^2 * k2 + b1 * k1 * rm + b1 * k2 * rm)/ters4
a = b1 + ip s
2
kt
b = ---------
rm + lm s
2
kt
a+b = b1 + ip s + ---------
rm + lm s
1 1
--- = ---------------------
a+b 2
kt
b1 + ip s + ---------
rm + lm s
2 2
rp rp
--- = ---------------------
a+b 2
kt
b1 + ip s + ---------
rm + lm s
s
d = -------
k1 + k2
2
s rp
e = c+d = ------- + ---------------------
k1 + k2 2
kt
b1 + ip s + ---------
rm + lm s
2 2 2
e = (k1 rm rp + k2 rm rp + kt s + b1 rm s +
2 2 2 2
k1 lm rp s + k2 lm rp s + b1 lm s + ip rm s +
3
ip lm s ) /
2
((k1 + k2) (kt + b1 rm + b1 lm s + ip rm s +
2
ip lm s ))
2 2
e = (k1 rm rp + k2 rm rp +
2 2 2
(kt + b1 rm + k1 lm rp + k2 lm rp ) s +
2 3
(b1 lm + ip rm) s + ip lm s ) /
2 2
(kt k1 + kt k2 + b1 k1 rm + b1 k2 rm +
(b1 k1 lm + b1 k2 lm + ip k1 rm + ip k2 rm) s +
2
(ip k1 lm + ip k2 lm) s )
rp vm
fuente = --------------------------------------
1 rm + lm s
kt (b1 + ip s) (--------- + ---------)
b1 + ip s 2
kt
kt rp vm
fuente = ------------------------------------------
2 2
kt + b1 rm + b1 lm s + ip rm s + ip lm s
v1 = (kt rp vm) /
2 2
(m1 s (kt + b1 rm + b1 lm s + ip rm s + ip lm s )
1 2 2
(---- + (k1 rm rp + k2 rm rp +
m1 s
2 2 2
(kt + b1 rm + k1 lm rp + k2 lm rp ) s +
2 3
(b1 lm + ip rm) s + ip lm s ) /
2 2
(kt k1 + kt k2 + b1 k1 rm + b1 k2 rm +
(b1 k1 lm + b1 k2 lm + ip k1 rm + ip k2 rm)
2
s + (ip k1 lm + ip k2 lm) s )))
v1 = (kt (k1 + k2) rp vm) /
2 2
(kt k1 + kt k2 + b1 k1 rm + b1 k2 rm +
b1 k1 lm s + b1 k2 lm s + ip k1 rm s +
2 2
ip k2 rm s + k1 m1 rm rp s + k2 m1 rm rp s +
2 2 2 2
ip k1 lm s + ip k2 lm s + kt m1 s +
2 2 2 2 2
b1 m1 rm s + k1 lm m1 rp s + k2 lm m1 rp s +
3 3 4
b1 lm m1 s + ip m1 rm s + ip lm m1 s )
v1 = (kt (k1 + k2) rp vm) /
2 2
(kt k1 + kt k2 + b1 k1 rm + b1 k2 rm +
(b1 k1 lm + b1 k2 lm + ip k1 rm + ip k2 rm +
2 2
k1 m1 rm rp + k2 m1 rm rp ) s +
2
(ip k1 lm + ip k2 lm + kt m1 + b1 m1 rm +
2 2 2
k1 lm m1 rp + k2 lm m1 rp ) s +
3 4
(b1 lm m1 + ip m1 rm) s + ip lm m1 s )
![]()

terw4=ip*lm*m
terw3=b1*lm*m+ip*m*rm
terw2=ip*k1*lm+ip*k2*lm+kt^2*m+b1*m*rm+k1*lm*m*rp^2+k2*lm*m*rp^2
terw1=b1*k1*lm+b1*k2*lm+ip*k1*rm+ip*k2*rm+k1*m*rm*rp^2+k2*m*rm*rp^2
terw0=kt^2*k1+kt^2*k2+b1*k1*rm+b1*k2*rm
1
a = ---------
b1 + ip s
rm + lm s
b = ---------
2
kt
1 s
c = --- + -------
m s k1 + k2
-------------
2
rp
2
k1 + k2 + m s
c = -----------------
2
(k1 + k2) m rp s
vm
fuente = --
kt
1
d = -----------------------------
2
(k1 + k2) m rp s
b1 + ip s + -----------------
2
k1 + k2 + m s
2
d = k1 + k2 + m s ) /
2
(b1 k1 + b1 k2 + ip k1 s + ip k2 s + k1 m rp s +
2 2 3
k2 m rp s + b1 m s + ip m s )
2
w1 = (k1 + k2 + m s ) vm) /
(kt (b1 k1 + b1 k2 + ip k1 s + ip k2 s +
2 2 2 3
k1 m rp s + k2 m rp s + b1 m s + ip m s )
rm + lm s 2
(--------- + (k1 + k2 + m s ) /
2
kt
(b1 k1 + b1 k2 + ip k1 s + ip k2 s +
2 2 2 3
k1 m rp s + k2 m rp s + b1 m s + ip m s ))
)
2
w1 =(kt (k1 + k2 + m s ) vm) /
2 2
(kt k1 + kt k2 + b1 k1 rm + b1 k2 rm + b1 k1 lm s +
b1 k2 lm s + ip k1 rm s + ip k2 rm s +
2 2 2
k1 m rm rp s + k2 m rm rp s + ip k1 lm s +
2 2 2 2
ip k2 lm s + kt m s + b1 m rm s +
2 2 2 2 3
k1 lm m rp s + k2 lm m rp s + b1 lm m s +
3 4
ip m rm s + ip lm m s )
2
w1 =(kt (k1 + k2 + m s ) vm) /
2 2
(kt k1 + kt k2 + b1 k1 rm + b1 k2 rm +
(b1 k1 lm + b1 k2 lm + ip k1 rm + ip k2 rm +
2 2
k1 m rm rp + k2 m rm rp ) s +
2
(ip k1 lm + ip k2 lm + kt m + b1 m rm +
2 2 2
k1 lm m rp + k2 lm m rp ) s +
3 4
(b1 lm m + ip m rm) s + ip lm m s )
e) Encontrar los parámetros del modelo matemático a partir de experimentos realizados con la planta mecánica.
m=.6;
kt=1/6.591;
k1=374.14;
k2=329.42;
rp=18.5e-3;
ip=12.49e-6;
rm=200;
lm=7.916e-3;
Tss=163.5e-3;
b1=(Tss*(k1+k2)*(rm*rp^2)-10*kt^2)/(10*rm) = 0.0038
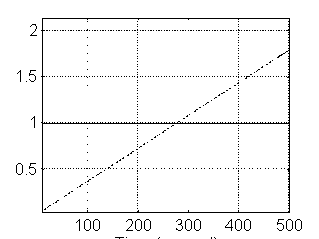
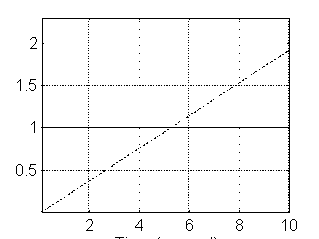
f) A partir del diagrama a bloques de SIMULINK, simular las dos salidas del sistema (posición angular q (t) y posición traslacional X(t) para una entrada escalón unitario (Vm) utilizando SIMULINK de MATLAB. Utilizar dos graficadores, uno para cada salida, cada uno con dos trazos, uno para la entrada y el otro para la salida correspondiente.
La siguiente figura es una gráfica de X1(t):
La siguiente figura es una gráfica de W 1(t):
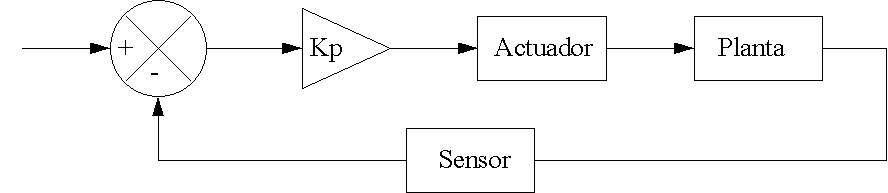
3. Implementación del sistema de control electrónico:
Para la planta construida, implementar un sistema de control electrónico retroalimentado con las siguientes características:
a) Utilizar amplificadores operacionales (OPAMPíS).
b) Como elemento de retroalimentación, utilizar alguna de las siguientes opciones:
C Alambre de nycromel a lo largo de la trayectoria y una escobilla en el carro.
C Un potenciómetro rotacional en el carro y una polea con un hilo de extremo a extremo de la placa soporte.
C Un potenciómetro rotacional en el carro y una polea contrada con una banda dentada en el piso de extremo a extremo de la placa soporte.
c) Como procesador, utilizar un control proporcional simple implementado con un amplificador inversor (para poder dar ganancias menores a 1).
d) Como actuador, implementar un arreglo PUSH-PULL clase AB con transistores bipolares y un amplificador operacional con la siguiente configuración:
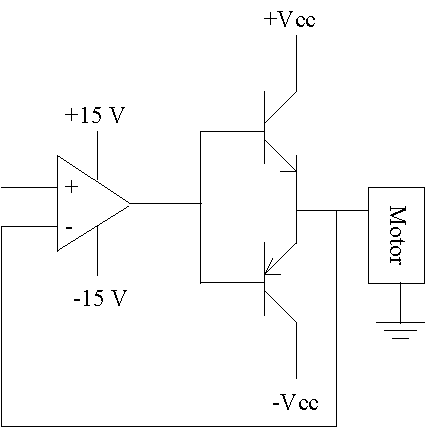
4. Análisis teórico del sistema:
El sistema tiene los siguientes polos:
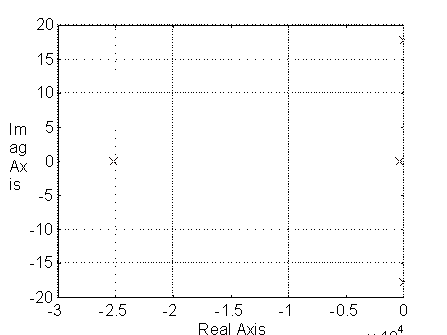
Y son:
1.0e+004 *
-2.5135
-0.0385
-0.0025 + 0.0018i
-0.0025 - 0.0018i
Para el sistema retroalimentado completo (controlador-planta):
a) Obtener la función de transferencia de lazo abierto del sistema (considerando un controlador porporcional) utilizando CACSD.
num=33.29 M
den= 1.0e+009 * (0.0000 S6 0.0000 S5 0.0110 S3 0.5171 S2 9.3384 S -0.0333)
Las raíces de den son:
1.0e+004 *
-2.5135
-0.0385
-0.0025 + 0.0018i
-0.0025 - 0.0018i
0.0000
b) Trazar el root locus del sistema utilizando CACSD.
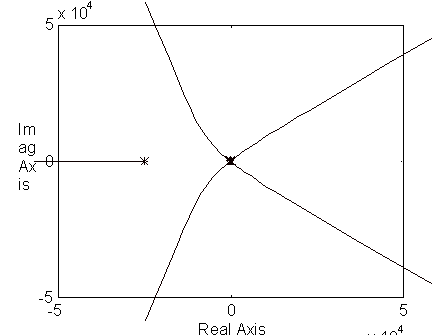
c) Concluir sobre el comportamiento de sistema al variar Kol desde 0 hasta infinito.
Para valores muy altos de Kol el sistema se hace inestable. El polo que se encuentra a la izquierda, por ser muy rápido, no tiene ninguna aportación al sistema.
Por otro lado, los polos complejos se alejan más rápido del cero que los reales, por lo que se puede concluir que aquéllos no dominan.
d) Encontrar los valores de Kol y de Kp (ganancia del controlador proporcional) para los cuales el sistema cambia de tipo de respuesta transitoria, o bien, para el cual el sistema se vuelve inestable (si existe).
e) Construir el diagrama a bloques en SIMULINK, utilizando variables para los parámetros, y bloques "subsistema" para el controlador y la planta. Utilizar un escalón unitario como entrada y definir "variables de regreso" hacia MATLAB para X1(t).
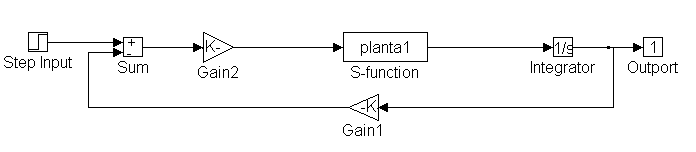
Planta 1 es:
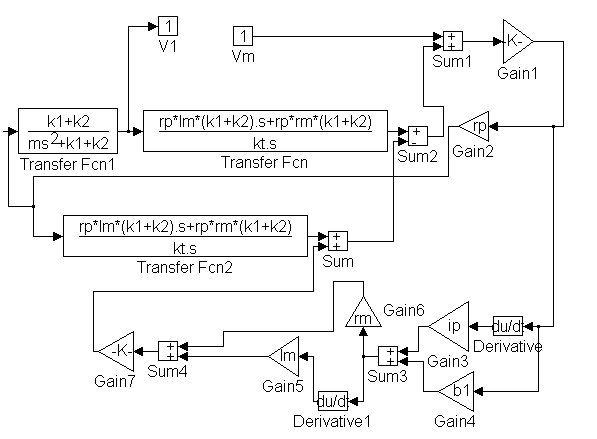
f) Simular el sistema desde MATLAB (utilizando la función "linsim"). Para Kol, asignar los valores que generan distintos tipos de respuestas según el root locus obtenido (asignar mínimo cuatro ganancias diferentes).
Cuando la ganancia es 140 la respuesta es:
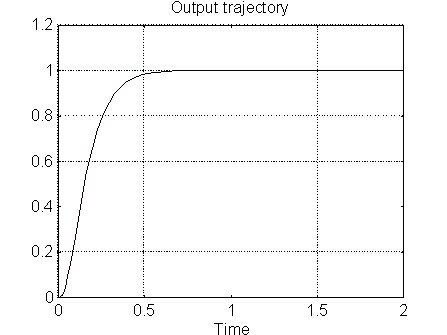
Cuando la ganancia es 200 la respuesta es:
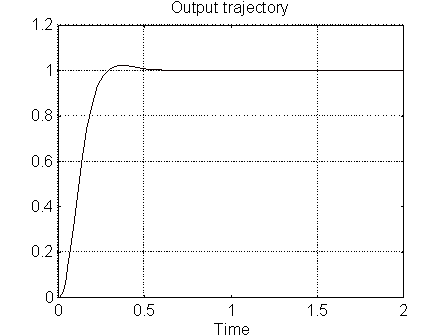
Cuando la ganancia es 1100 la respuesta es:
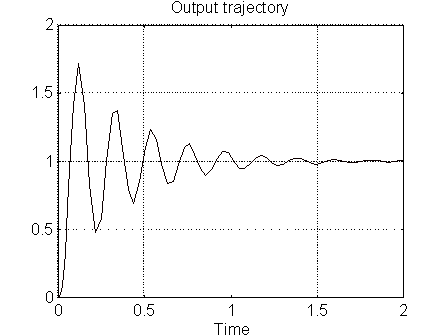
Cuando la ganancia es 1600 la respuesta es:
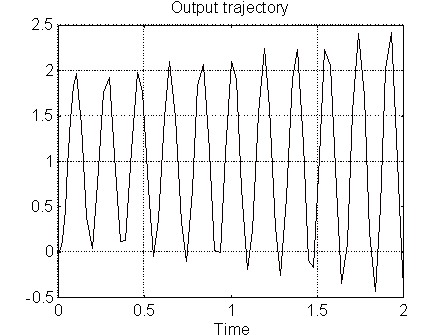
g) Utilizando una ganancia que genere una respuesta estable, alterar la masa del sistema al doble y a la mitad, y graficar la respuesta generada en cada caso por el simulador.
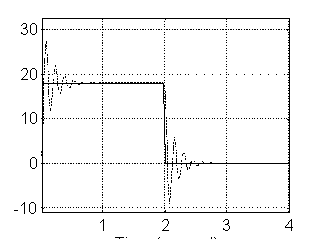
Con una Kol=1000 y m=0.6 Kg.:
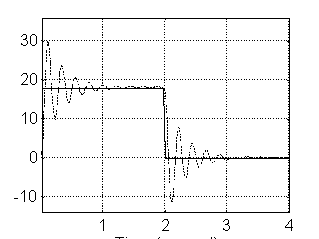
Con una Kol=1000 y m=1.2 Kg.:
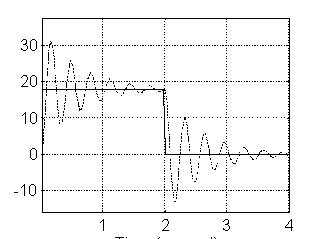
Con una Kol=1000 y m=0.3 Kg.:
5. Análisis experimental del sistema:
Para el sistema mecánico-electrónico construido (controlador-planta):
a) Concluir sobre las diferencias entre el comportamiento del sistema en el simulador de MATLAB y el comportamiento real, y enunciar las posibles causas y soluciones.
La resistencia en serie que vemos del motor, es diferente de la reflejada por el reductor, y como todas las mediciones fueron hechas sin tomar éste en cuenta, entonces la que debemos tomar es diferente.
En SIMULINK las ganancias son ideales, es decir no se saturan los componentes; por lo que el comportamiento que vemos al utilizarlo no es el real en cuanto a respuesta en tiempo, pero sí respecto a la amplitud y forma relativa. Al componer este problema usando bloques de saturación, obtenemos los tiempos reales, pero perdemos las formas y amplitudes.