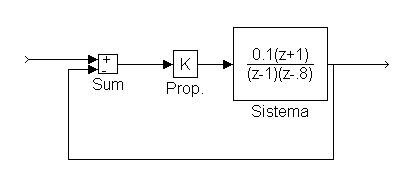
1.-Para el siguiente sistema:

a) Dibujar el Root-Locus:

           0.1 (1 + z)
G(Z) = -------------------
       (-1 + z) (-0.8 + z)

           0.1 + 0.1 z
G(Z) = ----------------
                      2
       0.8 - 1.8 z + z

numz=[.1 .1]

denz=[1 -1.8 .8]

rlocus(numz,denz)

zgrid

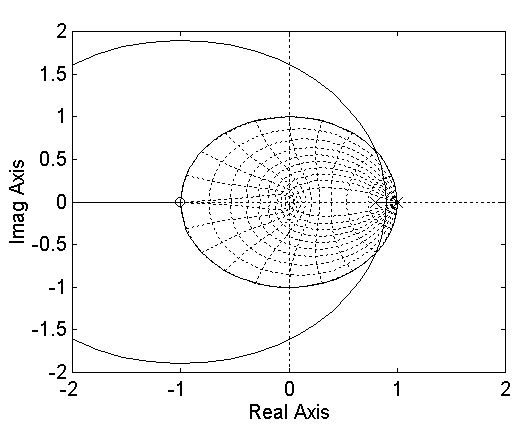
b) Encontrar el valor de k que coloque los polos de lazo cerrado sobre el eje real de tal forma que la respuesta a una entrada escalón alcance el estado estable en menos de 5T segundos. Escoger el valor de T.

Con un periodo de muestreo de un segundo:

T=1;

g=Together[ExpandAll[Together[.1 k(z+1)/((z-1)(z-.8))]]];

La funcion de transferencia en "S" queda:

z=(-2 -T s)/(T s-2);

Together[ExpandAll[Together[g]]]

       0.222222 - 0.111111 s
H(S) = ---------------------
                         2
        0.222222 s + 1. s

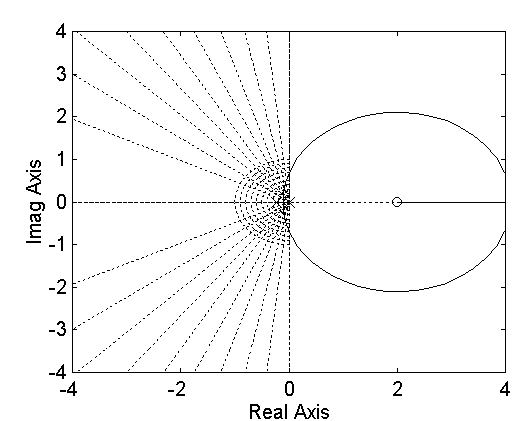
Root locus en "S":

nums=[-1/9 2/9]

dens=[1 2/9 0]

rlocus(nums,dens)

sgrid

       0.222222 k - 0.111111 k s
H(S) = -------------------------
                             2
            0.222222 s + 1. S

       0.111111 (2. k - 1. k s)
H(S) = ------------------------
                             2
            0.222222 s + 1. s

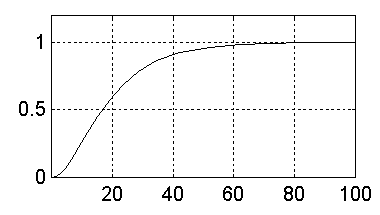
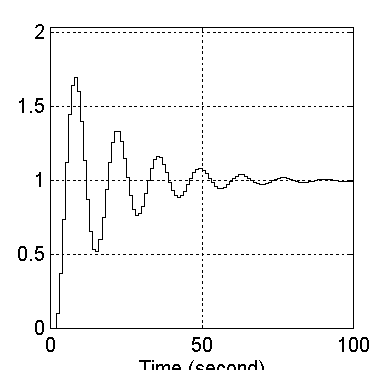
Respuesta del sistema digital con T=1seg y K=1 al escalón:

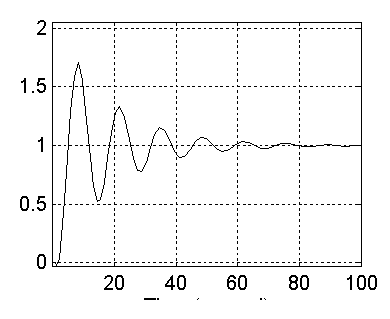
Respuesta del sistema analógico con K=1 al escalón:

Z = s +Wd J; s = x Wn; Wd = WnÖ (1-x ^2) = 0 (Sobre el eje)

Z = x Wn

Por otra parte, ts = 4.6 / x Wn = 5 T = 5 segundos; despejando: Z = x Wn = 4.6/5 = 0.92.

Z = 0.92
     |    0.1 (1 + z)    |
1 = k|-------------------|		k=0.05

     |(-1 + z) (-0.8 + z)|

Respuesta del sistema digital con T=1seg y K=0.05 al escalón:

Respuesta del sistema analógico con K=0.05 al escalón: