UNIVERSIDAD IBEROAMERICANA
Lab. de Electrónica Digital
Comparador 2-bits
Víctor Iniestra
Sergio López
13 Junio 1995
Comparador de 2 Bits:
Para el diseño del comparador se tomaron tres salidas importantes: Mayor que, Menor que e Igual a. Para la entrada X se tomó a A como la más significativa y a D como la menos significativa de Y. Con estas consideraciones llegamos a la siguiente tabla:
Entradas: Salidas:
X: Y: X<Y X=Y X>Y
A B C D
0 0 0 0 0 1 0
0 0 0 1 1 0 0
0 0 1 0 1 0 0
0 0 1 1 1 0 0
0 1 0 0 0 0 1
0 1 0 1 0 1 0
0 1 1 0 1 0 0
0 1 1 1 1 0 0
1 0 0 0 0 0 1
1 0 0 1 0 0 1
1 0 1 0 0 1 0
1 0 1 1 1 0 0
1 1 0 0 0 0 1
1 1 0 1 0 0 1
1 1 1 0 0 0 1
1 1 1 1 0 1 0
Estos datos se representan así en mapas de Karnaugh:
X<Y: A X>Y: A X=Y: A
0 0 0 0 0 1 1 1 1 0 0 0
1 0 0 0 D 0 0 1 1 D 0 1 0 0 D
C 1 1 0 1 C 0 0 0 0 C 0 0 1 0
1 1 0 0 0 0 1 0 0 0 0 1
B B B
Y las funciones lógicas que representan son:
X<Y: (¬A)(C)+(¬A)(¬B)(D)+(¬B)(C)(D)
X>Y: (A)(¬C)+(A)(B)(¬D)+(B)(¬C)(¬D)
X=Y: ¬((X<Y)+(X>Y))
Esta última función se puede escribir así ya que el no ser ni mayor ni menor implica ser igual.
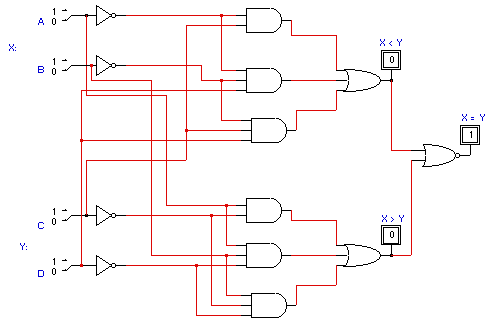
Así sería la realización lógica del comparador:

Sin embargo esta forma no es conveniente para la implementación física por el uso excesivo de inversores que requiere. Se opta entonces por una forma alterna y mayor simplicidad en la implementación (no así en la escritura):
X<Y: ¬( ((¬A)(C)) ((¬A)(¬B)(D)) ((¬B)(C)(D)) )
X>Y: ¬( ((A)(¬C)) ((A)(B)(¬D)) ((B)(¬C)(¬D)) )
X=Y: ¬((X<Y)+(X>Y))
Esto se consigue ya que ¬((¬”X)(¬Y))=(X+Y). Es decir los AND se cambian por NAND (AND normales pero cuya salida esta negada) y los OR se cambian también por NAND. El NOR de la función X=Y no se modifica.
Con esto tenemos funciones equivalentes pero más fáciles de armar:
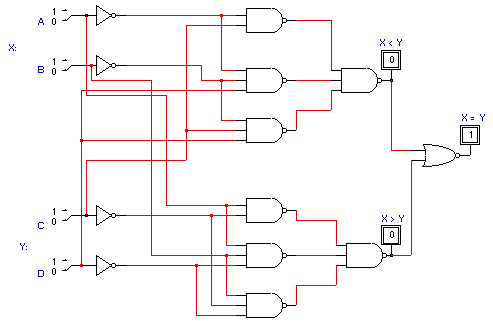
Comparador de 2 Bits:
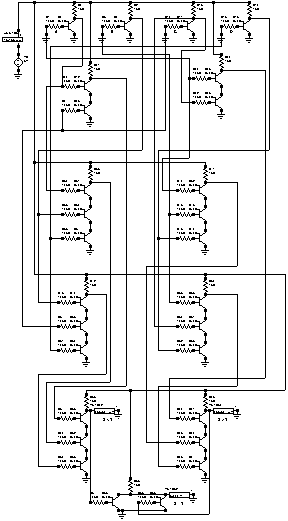
En la página anterior se vió el circuito eléctrico completo funcionando. Ahora veremos como a distintas entradas se obtienen las salidas esperadas y de paso veremos el consumo de energía.
Cuando X=00 y Y=00:
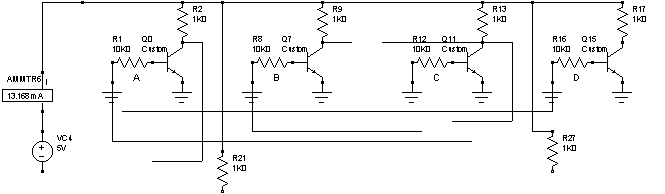
El voltaje de entrada de 0V se asegura con las tierras sobrepuestas en los alambres de entrada. Aqui como la corriente que sale del circuito es de 13.16mA el consumo de energía equivale a 65.8 mW.

Los voltajes de salida son los esperados: X<Y: 0
X=Y: 1
X>Y: 0
Cuando X=11 y Y=11:
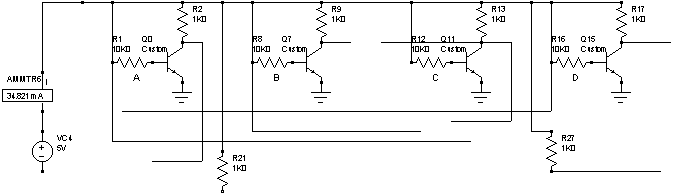
Los unos lógicos se aseguran mediante alambres a Vcc. Aqui la salida será la misma que en el caso anterior, pero el consumo de potencia es diferente debido a que las compuertas (todas) estan funcionando de distinta manera que en el caso anterior. El consumo de potencia es de 174 mA.
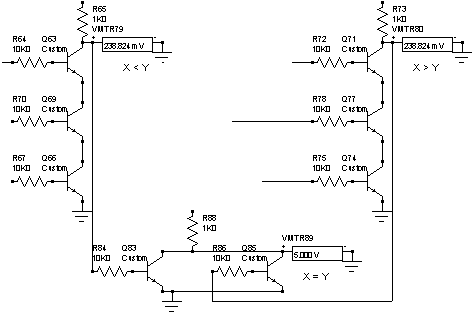
Para finalizar dos casos más:
X=11 Y=10
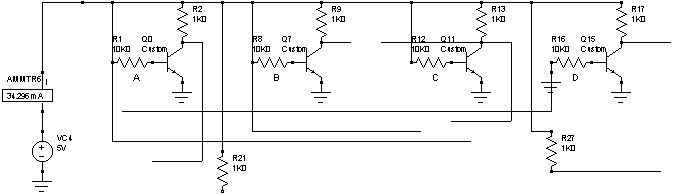
Potencia: 171mW
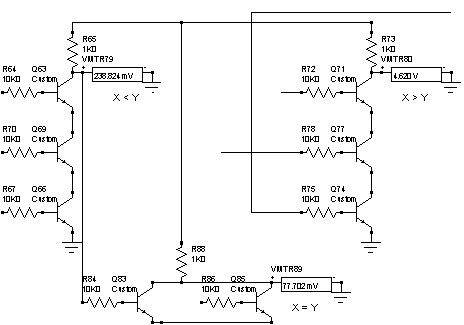
X=01 Y=10:

Potencia:146.mW
