Prof. Julio Cesar García Piña

Muchas importantes aplicaciones industriales de la probabilidad y de la estadística comprenden el control de calidad y la ingeniería de confiabilidad. El campo del control estadístico de calidad consiste en dos tipos generales de técnicas: tablas de control, para vigilar la actuación de un proceso de producción y muestreo de aceptación. En éste trabajo se analizarán estas técnicas. También se analizará la utilización de modelos probabilísticos para el análisis de confiabilidad, así como algunos aspectos de pruebas de duración.

1 Control estadístico de calidad

Todos los procesos de manufactura, por buenos que sean, están caracterizados por cierta cantidad de variación aleatoria que no puede eliminarse por completo. Cuando esta variabilidad está limitada solamente a variación aleatoria, se dice que el proceso se encuentra en un estado de control estadístico. Sin embargo, puede existir alguna otra situación en la cual la variabilidad del proceso se vea afectada también por alguna causa determinable, tal como un ajuste defectuoso de la máquina, error del operador, materia prima inadecuada, componentes desgastados en las máquinas y así sucesivamente. Por lo general, estas causas determinables de variación tienen un efecto adverso en la calidad del producto, de manera que resulta importante disponer de alguna técnica sistemática para detectar desviaciones importantes del estado de control estadístico, tan pronto como sea posible después de que ocurren. Con esta finalidad se utilizan principalmente las tablas de control.

Se distingue entre tablas de control para mediciones y tablas de control para atributos, dependiendo de que las observaciones acerca de la característica de calidad sea mediciones o enumeraciones de datos. Por ejemplo, puede elegirse medir el diámetro de un eje, mediante un micrómetro, y utilizar estos datos junto con una tabla de control para mediciones. Por otra parte, puede considerarse a cada unidad del producto como defectuosa o no defectuosa, y utilizar el recuento total de defectuosos junto con una tabla de control para atributos. Obviamente, ciertos productos y ciertas características de calidad se prestan al análisis mediante algunos de estos métodos, y puede resultar dificil la selección tajante entre los dos métodos.

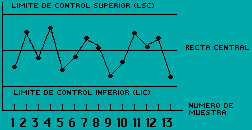
Una tabla de control, ya sea para mediciones o atributos, consiste en una línea central correspondiente a la calidad promedio a la cual debería funcionar el proceso cuando se encuentra presente el control estadístico, y dos límites de control, denominados límites de control superior e inferior. En la figura 1 se muestra una tabla común de control. Los límites de control se seleccionan de manera que los valores que queden entre ellos puedan atribuirse a variación aleatoria, en tanto que los valores que queden fuera de ellos puedan considerarse como indicadores de falta de control estadístico. El enfoque general consiste en obtener periódicamente una muestra aleatoria del proceso, calculando alguna cantidad adecuada, y graficando esa cantidad en la tabla de control, se investiga cuál pudiera ser la causa determinable de variación. Sin embargo, aun si un valor muestral queda entre los límites de control, alguna tendencia u otro patrón sistemático podrían indicar que resulta necesaria alguna acción, generalmente para evitar problemas más serios. Las muestras deberán seleccionarse de manera tal que cada una sea tan homogénea como sea posible, y maximizando al mismo tiempo la oportunidad para que se presenten variaciones debidas a una causa determinable. A esto generalmente se le denomina concepto de subgrupo racional. Son bases comúnmente empleadas para obtener subgrupos racionales, el orden de producción y la fuente (si existe más de una fuente).

Generalmente la capacidad para interpretar con precisión las tablas de control se adquiere con la experiencia. Resulta necesario que el usuario esté por completo familiarizado tanto con la base estadística de las tablas de control como con la naturaleza del proceso mismo de producción.

2 Tablas de control para mediciones

Al trabajar con una caaracterística de calidad que pueda expresarse como una medición, se acostumbra controlar tanto el valor promedio de la característica como su variabilidad. El control sobre la calidad promedio se ejerce mediante la tabla de control para medias, generalmente denominada tabla X. La variabilidad del proceso puede controlarse mediante una tabla R o una tabla σ, dependiendo de cσmo se estime la desviación típica de la población. Solo se analizará la tabla R.

Supóngase que la media y la desviación típica del proceso, denotadas μ y σ se conocen, y, ademαs, puede considerarse que la característica de calidad sigue la distribución normal. Sea X la media muestral basada en una muestra aleatoria de tamaño n proveniente de este proceso. Entonces se tiene una probabilidad de 1 - α de que la media de tales muestras aleatorias quede entre μ + Z_α/2(σ/Ö n) y μ - Z_α/2(σ/Ö n). Por tanto, podrían utilizarse estos dos valores como límites de control superior e inferior respectivamente. Sin embargo, por lo general no se conocen μ y σ y deben estimarse. Ademαs, tal vez no sea posible la consideración de normalidad. Por estas razones rara vez se utiliza en la práctica el límite de probabilidad 1 - α. Generalmente Z_α/2 se remplaza por 3, y se emplean límites de control de "tres sigma".

Cuando se desconocen σ y μ, por lo general se estiman en base a las muestras preliminares, tomadas cuando se considerσ el proceso bajo control. En ocasiones se utilzan de 20 a 25 o más, muestras preliminares. Suponga que se dispone de k muestras preliminares, cada una de tamaño n. Lo común es que n sea 4, 5 o 6; estos tamaños de muestra relativamente pequeños se utilizan ampliamente y aveces surgen a partir de la elaboración de subgrupos racionales. Sea X_i el tamaño de muestra para la i^ésima muestra. Después se estima la media de la población, μ, mediante la media total X = ΣX_i/k (1) Entonces, puede tomarse a X como línea central de la tabla de control X.

Es posible estimar a σ a partir de las desviaciones tνpicas o de los rangos de las muestras k. Ya que el método del rango es el que más se utiliza en la práctica, el análisis se limitará a este método. El tamaño de muestra es relativamente pequeño, de manera que hay poca pérdida de eficiencia al estimar a σ a partir de los rangos muestrales. La relación entre el rango, R, de una muestra proveniente de una población normal con parámetros conocidos y la desviación típica de esta población es necesaria. Puesto que R es una variable aleatoria, la cantidad W = R / σ, denominada rango relativo, tambiιn es una variable aleatoria. Los parámetros de la distribución de W se han determinado para cualquier tamaño de muestra n. a la media de la distribución W se le denota d₂, y una tabla de d₂ para distintos valores de n se proporcionan en la tabla I anexa. Sea R_i el rango de la i^ésima muestra, y sea R = ΣR_i/k (2) el rango promedio. Entonces, un estimador de σ serνa σ = R/d₂ (3). Por tanto, pueden utilizarse como límites de control superior e inferior para la tabla X

LSC = X + 3R/(d_2Ö n) LIC = X - 3R/(d_2Ö n) (4)

Se observa que la cantidad A₂ = 3R/(d_2Ö n) es una constante que depende del tamaño de la muestra, de manera que es posible escribir nuevamente la Ec. 4 como

LSC = X + A₂ LIC = X - A₂ (5)

La constante A₂ está tabulada para distintos tamaños de muestra en la tabla I anexa.

Los parámetros de la tabls R también pueden determinarse fácilmente. Es obvio que la línea central estará en R. Para determinar los límites de control, se necesita una estimación de σ_R, desviación típica de R. Nuevamente, considerando que el proceso está bajo control, la distribución del rango relativo W, será útil. La desviación típica de W, denotada σ_W, es una función n, la cual ya se ha determinado. Por tanto, puesto que R = Wσ es posible obtener la desviación típica de R como σ_R = σ_Wσ como σ es desconocida, puede estimarse a σ_R como σ_R = σ_WR/d₂ y podrían utilizarse como límites de control superior e inferior en la tabla R

LSC = R + 3σ_WR/d₂ LIC = R - 3σ_WR/d₂ (6)

Colocando D₃=1 - 3σ_W/d₂ D₄=1 + 3σ_W/d₂ puede volverse a escribir la ec. 6 como

LSC = D₄R LIC = D₃R (7)

en donde D₃ y D₄ están tabuladas en la tabla I.

Cuando se emplean muestras preliminares para elaborar los límites para tablas de control, se acostumbra tratar a estos límites como valores de prueba. Por tanto, los k medias y rangos muestrales deberian graficarse en las tablas adecuadas, y deberían investigarse aquellos puntos que excedan a los límites de control. Si se descubren causas determinables para estos puntos, deberán eliminarse y fijarse nuevos límites para las tablas de control. De esta forma, a la larga el proceso puede llegar a estar en control estadístico y con sus capacidades inherentes evaluadas. Entonces podrán considerarse otros cambios en la tendencia central y la dispersión del proceso.

3 Tablas de control para atributos

En ocasiones se desea clasificar un producto como defectuoso o no defectuoso en base a la comparación con una norma o estándar. Generalmente esto se hace para lograr economía y simplicidad en la operación de inspección. Por ejemplo, puede verificarse el diametro de un balero determinado si pasa a través de un calibrador consistente en perforaciones circulares cortadas en una plantilla. Esto sería mucho más sencillo que medir el diámetro mediante un micrómetro. En estos casos se utilizan tablas de control para atributos. Sin embargo, las tablas de control para atributos requieren de una tamaño de muestra considerablemente mayor que las tablas de control para mediciones. Se analizarán la tabla de fracción de defectos, o tabla p, y la tabla de defectos por unidad o tabla c. Obsérvese que es posible que una unidad tenga muchos defectos, y a la vez no sea ni defectuosa ni no defectuosa. En muchas aplicaciones una unidad podrá tener muchos defectos, y aun así clasificarse como no defectuosa.

Supóngase que D es el número de unidades defectuosas en una muestra aleatoria de tamaño n. Se considera que D es una variable aleatoria binomial con parámetro desconocido p. Ahora la fracción de defectos en la muestra en un estimador de p, esto es p = D / n (8). Además, la varianza del estadístico p es σ_p²=p(1-p)/n de manera que es posible determinar a σ_p² como σ_p² = p(1-p)/n (9).

La línea central y los límites de control para la tabla de control de fracción de defectos puede ahora determinarse fácilmente. Supóngase que se dispone de k muestras preliminares, cada una de tamaño n, y que D_i es el número de defectos en la i^ésima muestra. Entonces puede tomarse a p = ΣD_i/(kn) (10) como la línea central y a

LSC = p + 3 Ö ((p(1-p))/n) LIC = p - 3 Ö ((p(1-p))/n) (11)

como límites de control superior e inferior, respectivamente. Estos límites de control están basados en la aproximación normal a la distribución binomial. Cuando p es pequeña, la aproximación normal puede no siempre ser adecuada. En tales casos, es mejor emplear límites de control obtenidos directamente a partir de una tabla de probabilidades binomiales o, tal vez, a partir de la aproximación de Poisson a la distribución binomial. Si p es pequeña, el límite inferior de control puede ser un número negativo. Cuando esto ocurre, se acostumbra considerar a cero como el límite inferior de control.

En algunas situaciones puede resultar necesario controlar el número de defectos en una unidad de producto, en vez de la fracción defectuosa. En estas situaciones puede utilizarse la tabla de control de defectos por unidad. Supóngase que en la producción de tela resulta necesario controlar el número de defectos por yarda, o que al ensamblar un ala de avión deberá controlarse el número de remaches faltantes. Muchas situaciones de defectos por unidad pueden plantearse empleando como modelo la distribución de Poisson.

Sea c el número de defectos por unidad, en donde c es una variable aleatoria de Poisson con parámetro α. Ahora la media y la varianza de esta distribución son ambas α. Por tanto, si se disponen de k unidades y c_i es el número de defectos en la unidad i, la línea central de la tabla de control es c = Σc_i/k (12). Y

LSC = c + 3Ö c LIC = c - 3 Ö c (13)

son los límites de control superior e inferior, respectivamente.

4 Muestreo de aceptación

La inspección de un producto es una parte integral de todo proceso de producción. La situación general en la cual los productos, agrupados por lotes, se muestrean y los resultados de la muestra se utilizan para obtener inferencias referentes a la calidad del producto (o lote) se denomina muestreo de aceptación.

Es posible aplicar planes de muestreo de aceptación tanto a los bienes suministrados por los proveedores, antes de su utilización en otro proceso de producción, o a los resultados de uno de los propios procesos de producción de la compañía. La finalidad del muestreo de aceptación es estimar la característica pertinente de calidad de cada lote del producto e indicar si el lote deberá aceptarse o rechazarse.

Aun cuando el muestreo de aceptación generalmente se clasifica como una técnica de control de calidad, deberá señalarse que a veces no se ejerce ningún control directo sobre la calidad del proceso. Esto resulta especialmente verdadero cuando se está muestreando el suministro de algún proveedor y los lotes rechazados no se devuelven. Resulta obvio que siempre se logrará algún control indirecto a través de la comunicación con el fabricante.

Primero se considerará un procedimiento conocido como plan de muestreo único. El procedimiento consiste en obtener una muestra aleatoria de tamaño n proveniente de un lote compuesto de N elementos. Sea d el número de elementos defectuosos en esta muestra aleatoria. Entonces, si d<Q igual a un cierto número de aceptación, c, el lote se acepta. Puesto que N es fija el plan de muestreo está totalmente especificado por los parámetros n y c. Al procedimiento se le denomina plan de muestreo único debido a que se toma una desición en base a los resultados de una muestra. Si d>c, se rechaza el lote y existen varias posibilidades. Puede devolverse un lote rechazado al fabricante, en cuyo caso el plan de muestreo se denomina no rectificante. La calidad promedio que entra al proceso de producción es la misma que la calidad promedio que entrega el fabricante.

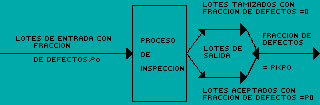
Por otra parte, pueden inspeccionarse el 100% de los lotes rechazados, ya sea reemplazando todos los elementos defectuosos con elementos correctos, o simplemente quitándolos. A esta alternativa se le denomina inspección de rectificación. La calidad promedio que entra al proceso de producción es superior a la calidad promedio que entrega el fabricante. Por lo tanto para una inspección de rectificación se considera la calidad promedio de salida proveniente del proceso de inspección. La calidad promedio de salida será alta cuando la calidad de entrada sea alta (pocos lotes de alta calidad se rechazan) como cuando la calidad de entrada es baja (muchos lotes de baja calidad se rechazan e inspeccionan). Puede mostrarse que la calidad promedio de salida tiene un límite inferior, denominado límite de calidad promedio de salida (LCPS).

Sin importar que tan mala sea la calidad de entrada, la calidad promedio de salida nunca será peor que el LCPS. Este proceso se ilustra en las figuras 2 y 3.

Cualquier plan de muestreo de aceptación puede describirse en términos de su curva característica de operación. En la figura 4 se ilustra una típica curva característica de operación para un plan de muestreo único. Esta curva relaciona la verdadera fracción de defectuosos para el lote con la probabilidad de aceptación. Se ha adoptado cierta terminología estándar para algunas características de un plan de muestreo, las que se presentan en la figura 4. El nivel de calidad que se considera "bueno" y que se desea aceptar la mayor parte de las veces se denomina nivel aceptable de calidad (NAC). El nivel que se considera "malo" y que debería rechazarse, la mayoría de las veces se denomina porcentaje de defectos de tolerancia de lote (PDTL). La probabilidad de que un plan de muestreo rechace lotes dentro del NAC se denomina riesgo del productor (α) y la probalidad de que un plan acepte lotes dentro del PDTL se denomina riesgo del consumidor (ί). Cualquier curva característica de operación puede definirse seleccionando los puntos (NAC, 1-α) y (PDTL/100, ß). La curva caracteristica de operación proporciona fundamentalmente las probabilidades de errores de tipo I y tipo II asociadas con el plan de muestreo.

El efecto de n y c en la curva característica de operación de un plan de muestreo único se presenta en la figura 5. Para N y n constantes se ve que aumentar c recorre a la curva característica de operación hacia a derecha; esto es, el plan se vuelve menos selectivo. Para N y c constantes, el aumentar a n hace que la curva característica de operación se vuelva más empinada. Si el tamaño de lote N es grande en relación con el tamaño de muestra n, la curva característica de operación en realidad independiente del tamaño del lote.

Pueden elaborarse planes de muestreo único ya sea para características de calidad de medición o de atributo. Puesto que cualquier plan de muestreo está definido por su curva característica de operación puede diseñarse un plan especificando dos puntos sobre la curva, por ejemplo (NAC, 1-α) y (PDTL/100, ß) y obtener los parámetros correspondientes del plan utilizando el modelo probabilístico adecuado. Para datos de atributos, el modelo probabilístico es la distribución binomial, aun cuando a veces se calculan probabilidades utilizando las aproximaciones de Poisson o la normal. Los planes de muestreo único para mediciones requieren que se especifiquen un tamaño de muestra y un límite único, o doble, para la media muestral. Generalmente el modelo probabilístico seleccionado es la distribución muestral.

Algunas veces, pueden lograrse tamaños promedio de muestra más pequeños (y, por lo tanto, reducciones en los costos de muestreo) sin pérdida de protección, utilizando planes de muestreo doble o múltiple. Se considerará brevemente el caso de atributos. Un plan de muestreo doble requiere que una muestra aleatoria de tamaño n₁ se tome del lote, y el número de defectos, denotado d₁, se anote. Si d₁<=c₁, el lote se acepta sin muestreo posterior. Si c₁<d₁<=c₂, se toma una segunda muestra aleatoria de tamaño n₂, y se anota el número de defectos d₂. Ahora bien, si d₁+d₂<=c₂, el lote se acepta; de otra forma se rechaza. La naturaleza de un plan de muestreo múltiple es semejante a la de un plan de muestreo doble, pero incluye más bien dos etapas. La ventaja de estos planes es que lotes de muy alta calidad serán aceptados en la primera muestra con una alta probabilidad, y lotes de muy baja calidad serán rechazados rapidamente, reduciendose así la cantidad promedio necesaria de inspección. Por otra parte, lotes de calidad "intermedia" pueden en realidad requerir de mayor inspección de la que se necesitaría con un plan de muestreo único. Además, el diseño y la administración de estos planes son más complicados que para planes de muestreo único.

El concepto de muestreo múltiple puede generalizarse a muestreo secuencial, en el cual se toma una decisión de aceptar, rechazar o continuar muestreando después de cada observación (esto es, todos los tamaños de muestra son uno). La elaboración de planes de muestreo secuencial requiere que se generen dos números de secuencias, denotados a_n y r_n, en donde n es el número de observaciones. Después el procedimiento sería rechazar el lote en cuanto el número de defectos exceda a r_n para alguna n. El muestreo continúa siempre y cuando el número de defectuosos obtenidos en n observaciones quede entre a_n y r_n.

5 Límites de tolerancia

En la mayoría de los procesos de producción se desea comparar un producto con un conjunto de especificaciones. Estas especificaciones denominadas generalmente límites de tolerancia, están determinadas por el diseñador o por el cliente. Algunas veces un producto se fabrica sin especificaciones previas, entonces se habla de límites de tolerancia "naturales" para el proceso. En cualquier caso los límites de tolerancia son sencillamente un conjunto de límites entre los cuales puede esperarse encontrar cualquier proporción dada, por ejemplo, P, de la población.

Si la distribución que sirve de base a la característica de calidad en cuestión y sus parámetros son conocidos, por ejemplo, debido a la experiencia prolongada, entonces resulta fácil establecer los límites de tolerancia. Por ejemplo si se sabe que una dimensión se distribuye normalmente con media μ y varianza σ², entonces pueden construirse lνmites de tolerancia para cualquier P. Si P=0.95, se ve que los límites de tolerancia son μ±1.96σ utilizando las tablas de la distribuciσn normal acumulativa.

Si se desconocen μ y σ², deberαn estimarse a partir de una muestra aleatoria denotándose X y S². Entonces resulta posible determinar una constante K tal que pueda afirmarse con un grado de confianza 1-α que la proporción de la población contenida entre X-KS y X+KS es al menos P. En la tabla II se proporciona una breve tabla de K para muestras aleatorias provenientes de poblaciones normales.