TeX : The Telephone Exchange Simulator

By

Vinay Jethava & Aneesh Dasgupta

Download Here

TeX is a multiple exchange simulator that calculates the number of lines required to be allocated per exchange based on the blocking probability desired and the inter-exchange traffic. The computation is based on Poisson's traffic statistics. It has been shown that poisson statistics accurately models the traffic at the exchanges in the absence of data ( i.e. only telephonic conversations and no internet connections.)

The telephone network allows a maximum of five exchanges currently. For planning involving more exchanges, we can assume that calls from exchange A₁ to A₆ are being routed from one of A₂, A₃, A₄ or A₅. Though a simplistic assumption, this nevertheless provides a reasonable guess towards the optimum solution. Further, telephone exchanges these days adapt their line allocation based on far superior estimation methods. This code just provides a reasonable guess into the numbers that come up during such a planning exercise. For a student of telecommunication at the undergraduate level, tweaking with the code and the resulting values can provide some interesting insights into the subject of telephony. A small amount of modification to the algorithm implementing the parotti distribution, and thereby incorporating data traffic, is something I plan to do soon.We (me & matka) enjoyed ourselves while writing this code, hope you do too.

The following cases can been simulated

Fixed line allocation

This model simulates a telephone exchange where the number of inter-exchange lines have been specified by the user. Thus, it calculates the blocking probability for a given fixed line allocation scheme. This was developed during initial algorithm testing and can be used to generate the M/M/N poisson statistics.

Dedicated inter-exchange incoming and outgoing line allocations

This model gives the optimum line allocation for the user defined parameters assuming dedicated incoming and outgoing lines from every exchange to the others. This means, say we require 1% blocking probability for calls from exchange A to exchange B and say 0.1% blocking probablility from B to A; the algorithm will calculate the number of lines required from A to B, say 10 and the number of lines from B to A, say 27.

Inter Exchange line pool

This model does not assumes dedicated incoming and outgoing lines. Lines allocated between two exchanges can be used by either exchange. Say we need a blocking probability of 1% from A to B and 0.1% from B to A, then it will allocate say 33 lines between A and B to achieve this. The older exchanges, in the good old days before fibre-optic cables, when the cost of cable overweighed the cost of exchange switches, this was indeed the way exchanges worked.

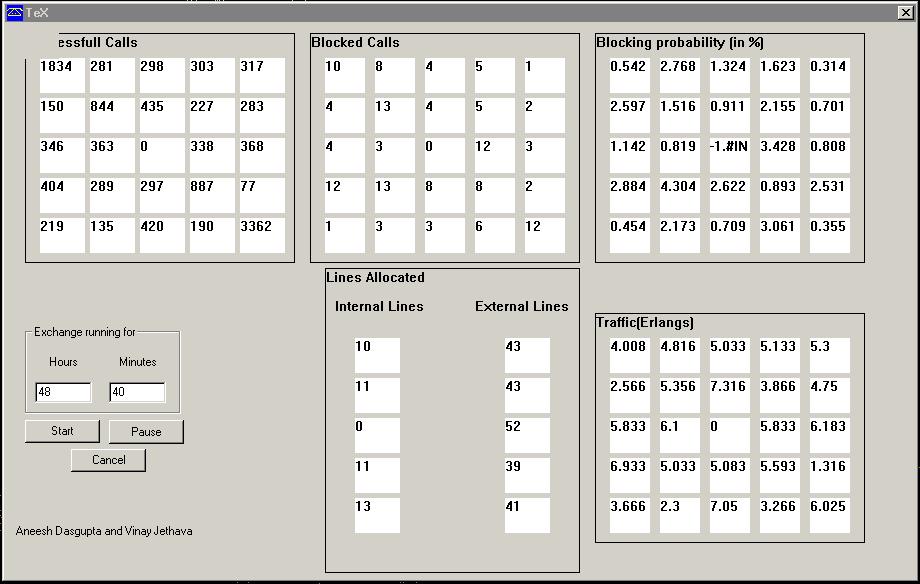
Line Pool

This model assumes two sets of lines: internal lines and external lines . any external line from the pool of external lines allocated to the exchange can be used to establish/recieve calls to/from any other exchange. This simulates the way modern exchanges work, when the cost of the exchange switch is the dominant factor.

TeX has been coded in Visual C++ 6.0 using MFC. The application alongwith the source code and the help files can be found at Download Here.