When an
objects positions changed with respect to time.VINAY"S PHYSICS REVISION NOTES IGCSE 2004 CHEMISTRY
BACK TO MAIN PAGE BACK TO CHAPTER INDEX CONTACT ME: vinz@india.com
Physics IGCSE Notes
o Measuring cylinders: use the bottom of the meniscus to determine the volume of water. Take note of intervals and units of measure
o Rules: use the point of the rule where mark is 0cm/m or if using another point, subtract final length from that point.
o Clocks: subtract final time from previous time. Take note of intervals
o Stopwatch: the double dots ( : ) separate the minutes from seconds. The third smaller number is the hundredth of a second.
Time: the interval between two events
Oscillation: complete to and fro movement e.g. oscillation of a pendulum or loaded spring
Period/Periodic Time: the time taken to complete one oscillation
Frequency: the number of complete oscillations made in one second. (This # is rounded to the nearest whole #) – Hz
Using the Pendulum (lead bob)
o Oscillation is the complete to and fro
o Calculate time taken for oscillations
o Period: time taken to move from one side, to the other side and BACK to the original side
o Oscillations have to be small
o Time taken to complete about 20 is recorded and then divided by 20 to obtain 1.
o The periodic time is proportional to the mass on the pendulum
1.2 Speed, Velocity and Acceleration
When an
objects positions changed with respect to time.
Types of motion:
o Linear
o Circular
o Rotational
o Random
o Wave
o Oscillatory/Vibrational
Distance: length of path traveled by an object
Speed x
Time
S.I.
UNIT = metre (m)
SCALAR
QTY
Speed:
The distance traveled per unit time
Distance/Time
S.I. UNIT =
m/sec
SCALAR
QTY
Average
Speed = Total Distance
Total Time Taken
Uniform/Constant Speed: When an objects rate of distance moved with time is
always the same.
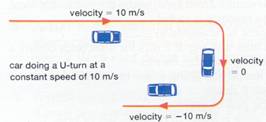
Velocity = the rate of change of distance moved with time in a
specified direction (rate of change of displacement)
Rate of
Change of Displacement = change in displacement
time taken
S.I.
UNIT = m/s
VECTOR
QTY
Average
Velocity = Total displacement
Total time taken
Uniform/Constant Velocity: When an object’s rate of change of displacement with
time is always the same.
Acceleration: the rate of change of velocity with time
Change in velocity (Final velo – Initial Velo)
Time Taken
S.I.
UNIT = m/s2
SCALAR
QTY
When an
object is slowing down, there is negative acceleration or retardation or
deceleration.
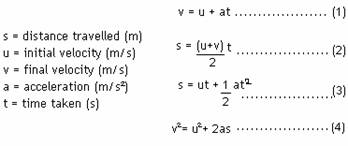Equations
of Uniformly Accelerated Motion (SUVAT)
When question is not complex, use:
Velocity-Time or Speed-Time Graphs
Show
Velocity of an object over time: used to obtain velocity of body and distance
traveled
POINTS:
1. Acceleration is any line moving vertical on graph – calculated with gradient of line.
2. Distance traveled is the total distance between x axis and boundary of lines.
3. Constant speed is a straight line (horizontal) through the graph.
4. Uniform acceleration is a straight line at an angle apart from 180˚. Steepness of slope determines magnitude of acceleration.
From the diagram:
(a) A car started from rest and accelerated uniformly to a velocity of 10m/s in 4s.
(b) It then traveled at a maximum velocity of 10m/s for ten seconds.
(c) The brakes were then applied and the car was uniformly retarded to rest 5s later.
Acceleration = Gradient of AB
Distance Traveled = (Area Triangle ABE) + (Area BCEF) + (Area Triangle FCD)
Average
Velocity = Total Displacement/Time Taken
An
object’s reluctance to move when at rest or to stop when in motion.
The
reluctance of an object to change its state of rest or state of motion.
Can be
overcome by force
Bigger
the mass, bigger the inertia (inertia depends on mass)
The
Force required to accelerate or decelerate and object
The
inertia of an object keeps it moving at constant speed in a straight line unless
an external force acts upon it. E.g. a thin piece of paper between a coin and a
bottle could be flicked off the bottle without the coin moving. Because the
force of friction between the paper and the coin acts for too short a time to
cause any appreciable damage.
Newton’s First
Law: everybody continues in its state of rest or of uniform motion in a straight
line unless compelled by some external force to act otherwise. .
Weight
a
planet’s gravitational pull on an object
S.I. UNIT =
Newtons (N)
1
Newton is the force required to give a mass of one kilogram an acceleration of
one metre per second2.
INSTRUMENTS : spring balance, compressive balance
VECTOR QTY
May
vary from one place to another on earth’s surface.
Gravity
on Moon = 1/6th the gravity on earth.
Weight
on earth in
Newtons = mass
x 10 (ad2g)
Newtons
= Mass in Kg x 10 (W = mg)
Mass
Qty
of matter in an object
S.I.
UNIT= kilogram (kg)
INSTRUMENTS = top-pan, beam, Buchart’s, lever arm } balance
SCALAR
QTY
Is
constant everywhere, the mass contained in an object cannot change.
Mass Weight
Constant everywhere may vary from place to place on earth’s surface
S.I. UNIT = kg S.I. UNIT = (N)
SCALAR QTY VECTOR QTY
Fundamental Base Qty Derived Base Qty
Measured: top-pan/beam/Buchart’s Measured: spring/compressive
The Amt of matter in object force due to pull of gravity (ie. Is a force)
Reasons why Weight differs from place to place:
The
earth’s geoid shape means certain places on earth’s surface are close to the
core (central point of gravity) e.g. north/South Poles than others e.g. Equator.
The closer bodies of mass are to the core, the more the attraction.
The
earth’s rotation on its axis means that some gravitational attraction will be
used to provide centripetal force to keep us in motion. At places e.g. North
Pole where there is no motion, weight of a body is greater.
A push or
pull that can be used to overcome the inertia of an object.
S.I. UNIT =
Newton (N)
INSTRUMENTS
= Spring Balance/Spring Dynamometer, (Newton-meter/Force meter)
Spring
Balance à
a spring whose extension is proportional to the force applied to it. Spring
calibrated by known forces (weights)
VECTOR QTY
(has direction)
Some effects
of forces:
o Cause a stationary object to move
o Cause a change in the direction of a moving object
o Can accelerate or decelerate a moving object
o Cause deformation of object
o Causes work to be done
o Produces a turning effect of a force
Types of
Forces:
o Friction: the force which opposes/restricts relative movement between two surfaces in contact.
o Gravitational Force: the force between two objects by reason of their masses.
o Electrostatic Force: the force between two charged objects at rest of the force between charged objects and uncharged objects.
o Centripetal Force: a centre-seeking force which causes an object to move in a circular path with a constant speed.
o Nuclear Force: a strong attractive force between nucleons in the atomic nucleus that holds the nucleus together.
o Electromagnetic Force: the force experienced by a current-carrying conductor or a moving charged particle in a magnetic field.
o Normal Reaction: an upward force exerted by a surface on an object placed on the surface and is at right angles to the surfaces in contact.
o Drag: The force which opposes the movement of an object in a fluid (gas/liquid)
o Centrifugal Force: a fictitious force (non-existent) exerted, as a reaction by the rotating object on whatever is providing its centripetal force.
o Cohesive Force: The intermolecular force of attraction between the molecules of the same material.
o Upthrust: an upward force exerted by a fluid on an object placed in it.
o Adhesive Force: intermolecular force between molecules of different materials.
o Weight: A planet’s gravitational pull on an object.
o Tension: the force experience by an object when it is subject to pulls at its ends.
o Compressive Force: An object is said to experience a compressive force when it is subject to pushes at its ends.
o Contact Force: the intermolecular force of repulsion between the molecules of two objects when they touch.
o Aerodynamic Force: Force exerted by a fluid on a curved object moving through that fluid as a result of the fluid flowing at different speeds on the surface of the curved object.
Elasticity
Deformation:
change in shape or size of object
Deforming
Agent:
physical property that can bring about deformation
Extension:
increase in length
Elastic:
if an object regains its original size after removal of an applied force. E.g.
rubber band, steel spiral spring.
To Demonstrate Extension
THE STRETCHING FORCE EXPERIMENT
Aim: to
determine extension of spring when known masses are hung.
Materials:
clamp and stand, boss, steel spiral spring, centimeter scale, scale pan,
standard weights, blue-tac and an optical pin (pointer)
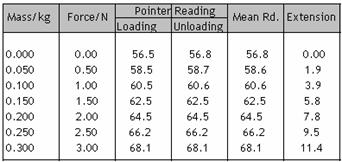Diagram (See above)
Table of
Values:
Graph:
eg. When
stated “A against B” then A is y axis and B is x axis.
Title, Label
Axis with S.I. Unit, Scale should cover 75% of graph, points plotted correctly,
best line through all points.
Table of
results on graph
Any key if
necessary
COMMON TITLE: Results of Stretching Spring Experiment. Graph showing extension (mm) against Load (N)
Calculate
Gradient : take two clear points and use: y2
– y1
X2 – x1
Some points
may be incorrect, prepare to mark them.
Use graph to
find certain Loads/Extensions
Hooke’s Law
States that:
providing the elastic limit is not exceeded, expansion of material is directly
proportional to the stretching force.
Elastic
Limit:-
the furthest point a string can be stretched to after which if it is stretched
any further, it will be permanently deformed.
Because
there was a straight line through the origin (see right) extension of spring is
directly proportional to the stretching force. (Hooke’s Law)
Using Hooke’s Law:
Example 1: The Extension of a spring when a load of 10N is hung is 4cm. What will be the extension when a load of 15 N is hung?
Hooke’s Law: F1 = F2
e1 e2
10N = 15N 10e = 60 e = 60/10 e2 = 6cm
4cm e2
Example 2: A spring is 20cm long when 10N is hanging and 30cm long when 20N is hanging. Draw diagrams to work out length of spring when a) No Load, b)5N load on it.
From Diagram:
F1 = F2 [Hooke’s Law]
e1 e2
10N = 20N
(20-x)cm (30-x)cm
(i) x = 10cm
(ii) 10N = 5N
10 e3
e3 = 5
Extension = 5cm, Length = 5 + 10 = 15cm
Physical Significance of Gradient of Spring
Gradient
represents the force constant or spring constant or stiffness of spring.
SYMBOL: K
Physical
Significance of Gradient of Spring for Expt = for every/to produce every cm on
the spring, a force of 0.25N is required.
F/e = k
(where k is proportionality constant, force constant, stiffness, spring
constant)
When two
forces act on a body with different magnitude in opposite direction along the
same line they constitute and unbalanced pair.
Motion is
always in the direction of the bigger force:
Net Force: the resultant force
after all deductions of imbalance has been made.
40.2 – 20.2
= 20N, 090° (40 + 80) – 100 = 20N, 090°
32.5 + 2.3 = 34.8N, 090° 45 – 5.1 = 39.9N, 180°
A diagram
showing all the force acting ON an object.
NOTE* does
not show forces of object on other things.
Examples:
F1 Ξ Force of String exerted on Bob
F2 Ξ Force of String 2 exerted on Bob
W Ξ Earth’s gravitational pull on Bob
F1 Ξ Frictional force exerted on the box
F Ξ Horizontal pulls of string on the box
W Ξ Earth’s gravitational pull on box
P Ξ normal reaction force of table on box
FD
Ξ
drag force exerted on ball
W Ξ Earth’s gravitational pull on ball
P Ξ normal reaction force of
knife edge on ruler
W Ξ Earth’s gravitational pull
on ruler.
FL Ξ Force exerted by load L1
on ruler.
Turning Forces & Moments
The moment
of a force refers to the turning effect of the force about a point.
Moment of
Force (Nm) = Force (N) x Perpendicular distance from pivot (m)
The turning
effect is the sensation that is felt or observed when a force acts at a certain
distance from the pivot. (Size and distance determine turning effect)
The further
away the perpendicular distance, the less force required to produce a certain
turning effect.
VECTOR QTY
Equilibrium
When an
object is balanced and total anti-clockwise moment = total anticlockwise moment
When there
is no resultant force and no resultant turning effect
Principle of Moments
In
equilibrium, total clockwise moments equals total anti-clockwise moments about
the same point.
PRINCIPLE OF MOMENTS EXPERIMENT – TO VERIFY
The ruler is balanced at its c.g
and unequal masses are hung from cotton loops on either side of the rule and
their distances from the pivot are adjusted until the rule becomes balanced
again. It is then repeated with various lengths and weights and results
tabulated.
Allowing for
experimental error, it is seen that in every case the product of force x
perpendicular distance on left is equal to force x perpendicular distance on
right.
CONC: when a
body is in equilibrium, the sum of the anticlockwise moments about any point is
equal to the sum of the clockwise moments.
Applying Principle of Moments:
M kg x 20.5cm = 45cm x 0.1 kg
M kg = 4.5 kg cm
20.5 cm
=0.22
kg
Applying the principle of moments:
WN x 25cm = (15cm x 4N) + (40cm x 1N)
WN = 60 + 40
25
W = 4N
Centre of Gravity (c.g)
The point on
that object where its total weight seems to act.
It is
usually near its middle/centre of an object. (coincides with centre of mass)
A plumbline
(a small bob supported by a thin inextensible string), always hangs vertically
below the point of suspension because the string sets in a vertical direction
indicating the force of gravity acting on it.
Used for
testing uprightness of walls, pillars and structures in construction.
PLUMBLINE EXPERIMENT
To determine
centre of gravity of an irregular lamina using a plumbline
Irregular
lamina with three pin holes, plumbline, Clamp and stand, inextensible thread,
piece of cork with pin stuck in cork, ruler, and pencil.
The lamina
was hung freely on all holes in turns on the pin with a plumbline directly in
front. A pencil was used to draw the lines on the card that the plumbline
created. The card was removed and three holds and lines were observed.
Three straight lines through the
holes intersected at a common point.
The point of
intersection of the three straight lines through A,B and C is the centre of
gravity of the irregular lamina.
To verify
that it is the centre of gravity, the point is balanced on the sharp tip of an
object e.g. Pencil, and the entire lamina balances.
Used to show
that the centre of gravity of triangular lamina lies at the point of
intersection of its medians.
Stability
o Stable equilibrium: plumbline is pushed to one side, its centre of gravity rises and gravity tries to pull it back to its lowest position
o Unstable equilibrium: ruler balanced on finger, if it moves slight, c. of g. falls and continues falling.
o Neutral equilibrium: ball on pool table: if it moves left or right, centre of gravity does not rise or fall.
To make an object more stable, it must have:
A low centre of gravity and a wide base
The capacity
or the ability to do work
S.I. UNIT =
Joules (J)
SCALAR QTY
Forms of
Energy :
o Electrical
o Heat/Thermal Energy
o Sound Energy
o Chemical Potential Energy (stored in food/fuels, petrol, bread, batteries)
o Nuclear (stored in the nucleons in an atom)
o Mechanical Energy
o Light Energy
o Electro-magnetic
o Geothermal
o Wave
o Tidal
o Wind
Mechanical
Energy :
o Kinetic Energy (moving object)
o Gravitational Potential Energy (stored in water in dam)
o Elastic Potential (Strain Energy) – stored in the elastic of a stretched material
Principle of
Conservation of Energy: Energy can be transformed from one form to another but
it cannot be created or destroyed. (amount stays the same)
Energy Processes:
a) A boy uses a catapult to shoot a bird:
b)
Dry cells are used to power a
torchlight:
Newton’s Second Law
The greater
the force on an object, the greater the acceleration
The greater
the mass the lower the acceleration
Thus N.S.L =
F = ma
Resultant
Force (N) = mass (kg) x acceleration (m/s2)
THERFORE, 1N
is defined as the force which gives to a mass of 1kg, an acceleration of 1m/s2.
Note: weight
= mass x 10m/s2 (acceleration due to gravity)
When F = ma,
then F = m (v – u)
T
So, F x t = mv – mu (IMPULSE)
Kinetic Energy: energy possessed by an object by reason
of its motion.
1 mv2 Joules
2
Potential Energy:
o GRAV: energy stored in an object by reason of its rest position in a field of force (gravitational)
§ P.E. grav = mgh (where h – height above reference point)
o ELASTIC: energy stored in an object by reason of its molecules (elastic)
§ P.E. elast = 1 ke2 (where k = force constant and e = extension)
2
§ Is also average force (N) x distance metres (= Energy Transferred (work done)
Work
movement
against an opposing force
energy
transferred
S.I. UNIT =
Joules (J) or Newton-Meter (Nm)
SCALAR QTY =
Force (N) x Distance Moved In direction of Force (metres)
Kilojoules =
Joules / 1000
Mega joules
= Kilojoules / 1000
1 joule is
the work done when a force of 1newton moves through 1 metre (in the direction of
the force.
Example 1: A man lifts a brick of mass 5kg from the floor to shelf 2 metres high.
Work done = force x distance
Work = (5kg x 10) N x 2 metres
= 100J
Example 2: A girl weighing 500N climbs 40m vertically when walking up the stairs in an office block. How much work done against gravity?
Work = force x distance
Work = 500 x 40
= 20,000 J = 20KJ
Example 3: A man uses 20J to lift a pencil from the desk. How much work is done? 20J
Example 4: A car of mass 800kg is traveling at 10m/s. It comes to rest 8m later when the brakes are applied. What is the average force exerted by the brakes?
Since energy is conserved, K.E. of car is transferred to braking energy.
Work Done = Energy Transferred
Work = K.E.
Force x Distance = ½ mv2
Force = ½ 800 x 1000/8
= 5000N
Power
the rate of
working (rate of transferring energy)
SCALAR QTY
S.I. UNIT =
Watt (W) or Joules per sec (J/s)
Power (W) =
work done/energy transferred (J)
Time taken (s)
I kW = 1000
watts
1 MW = 1 000
000 watts
Example 1: A crane lifts a load weighing 3000N through a height of 5m in 10 seconds. What is the power of the crane?
(Work done = force x distance moved)
Time taken
3000N x 5m
10
=1500W
=1.5kW
1 watt is a
rate of working 1 joule per second.
In 1 second,
a light bulb transfers 3 joules to light energy and 57J to heat.
a) Energy input per second = 57 + 3 = 60J
b) Efficiency = 3/60 = 0.05%
Total Energy input
Pressure =
magnitude of force
Area on which force acts
S.I. UNIT =
N/m2 or Pascal (Pa)
SCALAR QTY
A force
acting over a small area gives a large pressure
An
elephant’s foot exerts a high force but a girl’s heel exerts a larger PRESSURE
because of its smaller area. (Her heel would sink further into the ground)
The smaller
the area, the larger the pressure:
Evidence:
Case 1: An elephant weighing 40 000N stands on one foot of area 1000 cm2
Pressure = force / area
= 40 000N/ (0.1) m2
= 400 000 N/m2
Case 2: A girl weighing 400 N standing on one stiletto heel of area 1cm2
Pressure = force/area
= 400N/0.00001
= 4 000 000 N/m2
Example 1: Calculate the lowest and the highest pressure of the below object if it weighs 100g
a)
Highest pressure = smallest side =
light gray side
Pressure = force/area
= 1N/(1.0 x 0.5)
= 2.0 N/m2
b) Lowest Pressure = largest side = white side
Pressure = force/area
= 1N/(1.0 x 2.0)
= 0.50 N/m2
Pressure in Liquids
Transmitted
throughout liquid
Acts in all
directions
o EXPT (Evidence): Several holes poked in a polythene bag. Bag squeezed top bottom sides; water squirts out in all directions.
Pressure
increases as depth of liquid increases
o EXPT (Evidence): Tall water container w/ 3 holes of equal size 1 at tope, 1 middle, 1 at bottom. The bottom hole squirts out water at the greatest horizontal distance from the container followed by the centre and then the top hole.
Pressure in
liquid (in terms of depth) = hóg.
Where h º
depth (m), ó
(row) = density (kg/m), g
º
acceleration due to gravity (10m/s)
\
Factors affecting pressure of liquid at a given place:
o depth
o density
E.g. a dam
built with thicker walls as goes down so walls can withstand greater pressure at
bottom of lake.
Density of
Water = 1g/cm or 1000kg/m
Liquids
stand at the same levels in each tube whether slanted “it find it’s own level”
In order for
an object to sink in a fluid, the density of the object must be greater than the
density of the fluid.
Upthrust is
the resultant force acting upward on a body when pressure acting on the body is
higher at the bottom than at the top when displaced in a fluid.
Atmospheric Pressure
The
atmosphere around us exerts this pressure
It is
roughly ( »)
100 000 Pa (Pascals or N/m)
It is
measured by the barometer.
Standard
Atmospheric Pressure = 760 mmHg or 76 cmHg or 0.76mHg
E.g. when
you suck on straw, atmospheric pressure pushes the liquid up into your mouth.
Shape of
meniscus is “Ç”
because mercury does not wet.
Column of
mercury held or supported by atmospheric pressure (height varies with A.P)
To show how
mercury can tell pressure:
o Standard a.t.p = 0.76mHg
o Depth = 0.76m
o Pressure in Liquids = hóg
= (0.76m x 136000kg/m x 10m/s) = 103,360 Pa
» 100, 000 Pa
*Density of Mercury = 136 000 kg/m
THE COLLAPSING/CRUSHING CAN EXPERIMENT
Boiling
Water poured into container, water evaporates taking all molecules of air out.
Atmospheric Pressure (outside) Atmospheric pressure is greater than pressure
equals pressure on inside walls of can. on inside walls of can, thus, can crush.
Pressure
Gauges:
o Bourdon Gauge
o
Manometer
(lung pressure, gas pressure)
o Aneroid Barometer
Water Manometer
Used to
measure pressure of gas supply by using relative difference in levels of water
in two arms.
When both
arms exposed to atmosphere, same pressure applied
à
to left and right (water surface) – same horizontal level.
h
= difference in levels.
ó
= density of liquid in tube, g = 10m/s
When gas tap
turned on, gas exerts pressure on water such that gas pressure is greater than
atmospheric pressure
The level of
water dropped on the right side equal an increase the level on the other side.
\
the height is double what the water level on the right has dropped.
*AT ANY
PARTICULAR TIME, H REPRESENT THE DIFFERENCE IN PRESSURE BETWEEN ATMOSPHERIC
PRESSURE AND GAS PRESSUR CALCULATED BY hóg.
\Gas Pressure = AP – Diff. in Pressure]
\ Gas Pressure = AP + Diff in Pressure
PASCAL’S PRINCIPLE
When
pressure applied to surface of fluid, it is transmitted equally throughout the
fluid.
HYRDRAULIC MACHINES
Small force
applied to small piston to produce pressure.
Pressure it
transmitted equally through the liquid (that is in contact with pistons)
Same
pressure reaches larger piston to create larger force
Pressure
at small piston = pressure through liquid = pressure at large piston
Small
ForceA
= Large ForceB
AreaA AreaB
To calculate
pressure through liquid force/area at piston.
A hydraulic
machine e.g. hydraulic car jack, moving arms on a mechanical digger.
Hydraulic Disc Brakes
When driver’s foot steps on brake, small piston exerts pressure through the entire body of liquid. Pressure transmitted to pistons on each side of large disc on axle. Pressure makes pistons squeeze the disc to slow down car. Since pistons are large, force applied to large discs are also large. (Driver’s pressure is ‘magnified’ by increased area of pistons).