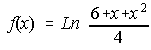
-- APLICACIONES DE LA DERIVADA --

1. Sea la función f(x), se pide: a) Dominio de f(x). b) Máximos y mínimos relativos. (Junio 89)

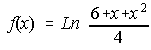
2. Calcula los máximos y mínimos de la función f(x). Estudia su crecimiento.

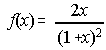
(Junio 89)

3. Calcula los extremos relativos y absolutos de f(x)=|3+2x-x²| en el intervalo [-2,4].

(Septiembre 91)

4. Estudia el crecimiento y decrecimiento de la función f(x). Calcula los máximos y mínimos relativos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( Junio 92 )

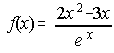
5. Estudia el crecimiento y decrecimiento de f(x)= x²Lnx. Obtén sus máximos y mínimos relativos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( Junio 93 )

6. Halla los intervalos de crecimiento y decrecimiento, máximos y mínimos de la función y= x.e^x.

7. Estudia el crecimiento y decrecimiento de la función siguiente, según los valores de m:

8. Halla los máximos y mínimos relativos de las siguientes funciones:

a) y=(x²+1)/(x-1) ; . . . . . b) y= (x³-4x²+7x-6).e^x ; . . . . . c) y= x.e^-x ; . . . . . d) y=e^x/x²

e) y= x³-9x ; . . . . . . . . . . f) y= x⁴.e^x ; . . . . . . . . . . . . . . . . g) y= sen⁴x

9. Determina el máximo y el mínimo de la función f(x)= x⁵ + x + 1 en el intervalo [0,2].

10. Dada la función f(x)= ax³+bx²+cx+d, halla el valor de "a, b, c y d" para que tenga un máximo en el punto M(-2,21) y un mínimo en el punto M'(-1,6).

11. Se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 800 pts/m y la de los otros 100 pts/m, halla el área del mayor campo que pueda cercarse con 288.000 pts.

12. Halla las dimensiones del rectángulo de área máxima inscrito en una circunferencia de radio 5.

(Junio 89)

13. Un jardinero ha de construir un parterre en forma de sector circular de perímetro 20 m. ¿Cuál será el radio del parterre de área máxima? ¿Cuál será la amplitud en radianes del sector?

14. Los barriles que se utilizan para almacenar petróleo tienen forma cilíndrica y una capacidad de 160 litros. Halla las dimensiones del barril para el que la chapa empleada en su construcción sea mínima.

15. Una hoja de papel debe contener 18 cm² de texto impreso. Los márgenes superior e inferior deben tener 2 cm y los laterales 1 cm. Calcula las dimensiones de la hoja para que el gasto de papel sea mínimo.

16. Dos antenas de televisión separadas 10 m. son fijadas al suelo mediante un único cable tensor. Si el cable se ata a 4 m de altura en una antena y a 7 m en la otra, se desea conocer el punto de fijación del cable en el suelo de forma que la longitud del cable sea mínima.

17. Halla los puntos de la curva y² = 6x cuya distancia al punto (4,0) sea mínima.

18. De todas las rectas que pasan por (2,3), ¿cuál determina con los ejes un triángulo de área mínima?.

19. Se considera una ventana rectangular en la que lado superior ha sido sustituido por una semicircunferencia. Sabiendo que el perímetro de la ventana es 6 metros, halla las dimensiones de la base y la altura del rectángulo para que la superficie de la ventana sea máxima. . . . (Prop. 2.001)

20. Estudia el crecimiento y la concavidad de la función f(x). . . . . . . . . . . . . . . . . . . . . . (Junio 91)

21. Calcular los intervalos de concavidad, convexidad y los puntos de inflexión de la función f(x):

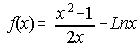
22. Calcula los puntos de inflexión de f(x)= x⁴ -4x³ +12x -12. Escribe la tangente a f(x) en uno des sus puntos de inflexión. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 92)

23. Halla los intervalos de concavidad y convexidad así como los puntos de inflexión de la función f(x)= (x-1)e^x.

24. Determina los intervalos de concavidad y convexidad y los puntos de inflexión de las siguientes funciones:

; . . . . . . . . . . . . . ; . . . . . . . .

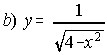; . . . . . . e) y= x³.(x-1)⁴ ; . . . . . . . . . . . . . f) y= x².Lnx

25. Dada la función se pide: a) Campo de existencia. b) Asíntotas

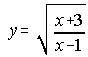
(Septiembre 89)

26. Dada la función siguiente estudia: a) Asíntotas ; b) Simetrías ; c) Crecimiento y decrecimiento d)Máximos y mínimos ; e) Puntos de inflexión f) Puntos de corte con los ejes. . . . . (Septiembre 90)

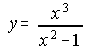
27. Determina cuales de las siguientes funciones son pares, impares o periódicas:

a) f(x)= senx ; . . . . . b) f(x)= sen²x ; . . . . . c) f(x)= 2 + cos²x

d) f(x)= | x³ |+ 2 ; . . . . e) f(x)= | tagx | ; . . . . . f) f(x)= cosx²

28. Dibuja la gráfica de las siguientes funciones:

1) y= x³-6x²+12x+4 ; . . . . . . 2) y=|x³-3x²+3x-1| ; . . . . . . . . 3) y= x²-x⁴

29. Representa gráficamente las siguientes funciones:

a) y= Ln(x+2) ; . . . . . 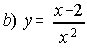; . . . . . 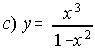; . . . . . d) y=| x⁶ - 16x² |

; . . . . . f) y= x.e^1/x ; . . . . . . . g) y= xe^x ; . . . . . . . . h) y= x²Lnx

i) y= sen²x ; . . . . . . . ; . . . k) y= (1-x)e^x ; . . . .

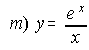; . . . . . . . n) y= e^senx ; . . . . . . . . ñ) y= x^x ; . . . . . . . . . .

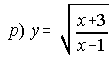; . . . . q) y=Ln(x²-4) ; . . . . r) y= senx + cosx ; . . .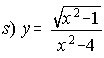

30. Sea f(x) la función siguiente, determina:

a) Intervalos de crecimiento y decrecimiento, así como los extremos de f.

b) Rectas asíntotas a la gráfica de la función f.

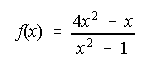
SOLUCIONES

1. a) R . . . . b) x= -1/2 mínimo

2. Crece en (-1,1) y decrece en (-inf,-1)(1,inf). Máximo en x=1.

3. Mínimos absolutos en x=-1 y x=3. Máximos absolutos en x=-2 y x=4. Máximo relativo en x=1.

4. Crece:(1/2,3). Decrece:(-inf,½)u(3,+). Mínimo en x=1/2. Máximo en x=3

5. Crece en (0'6065,+inf) Decrece en (0,0'6065). Mínimo relativo en 0'6065.

6. Crece : (-1,+inf). Decrece (-inf,1). Mínimo relativo en x=-1.

7. Si m<0 crece en R-{1}. Si m>0 decrece en R-{1}.

8. a) Máx en x=-0'4142. Mín en x=2'4142. . . . . b) Mínimo en x=-1. . . . . c) Máximo en x=1.

d) Mínimo en x=2. e) Máx en : x=. Mín en : x=0 y x=±3.

f) Mínimo en x=0 y máximo en x=-4.

g) Máx relativos en x=(2K+1).pi/2 y mín en x=K.pi, siendo K un número entero.

9. Mín absoluto en x=0 y máx absoluto en x=2.

10. a=30, b=135, c=180, d=81

11. El lado del camino vale 160 m. y el otro lado 720 m.

12. Cuadrado de lado l=7'0711. . . . . . . . . . . . . . . 13. R=5, = 2 radianes.

14. R=2'.942. h=2R . . . . . . . . . . . . . . . . . . . . . . . 15. Los lados valen 5 cm y 10cm.

16. A 3'7 m. de la antena de 4 m. . . . . . . . . . . . . . 17. P(1,2'4495) y Q(1,-2'4495)

18. . . . . . . . . . . . . . . . . . . . . . . . . . . . 19.

20. Crece: (0,e). Decrece (e,inf). Máx en x=e. Cóncava hacia abajo en (0,e^3/2). Cóncava hacia arriba en (e^3/2,). Punto inflexión en x=e^3/2.

21. Cóncava hacia abajo en (0,1). Cóncava hacia arriba (1,inf). Punto de inflexión en x=1.

22. x=0 ; x=2 Tangente en x=0: 12x -y -12=0 Tangente en x=2: 4x + y -4 =0

23. Cóncava hacia abajo en (-inf,-1). Cóncava hacia arriba en (-1,+inf). P. inflex. en x=-1.

24. a) Cóncava hacia arriba en R. . . . . . . . . . b) Cóncava hacia arriba en su dominio.

c) Cóncava hacia arriba en (0,inf). . . . . . . . . d) P.inflexión en y en .

e) Cóncava hacia abajo: (-inf,0)u(0'2265,0'6306). Cóncava hacia arriba: (0,0'2265)u(0'6306,+inf)

f) Cóncava hacia abajo en (0,e^-3/2). Cóncava hacia arriba en (e^-3/2,)

25. Dominio= (-inf,-3]u(1,inf) A.v.: x=1 A.h.: y=1

26. a) A.V: x=-1, x=1. A.O. y=x . . . . . . . . b) Impar

c) Crece en (-inf,-1'7321)u(1'7321,inf) ; Decrece: (-1'7321,-1)u(-1,1)u(1,1'7321)

d) Máx:x=-1'7321 , Mín: x=1'7321 . . . . . . . e) P.I.x=0 f) (0,0)

27. a) Impar ; . . . . . . b) par ; . . . . . c) par ; . . . . . . d) par ; . . . . . . e) par ; . . . . . . f) par

30. a)Decrece en. Crece :

Máx en y mín en . . . . . . . . . b) A.v.: x=1 y x=-1. A.h: y=4.