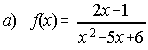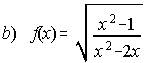-- CONTINUIDAD --

1. Resuelve las ecuaciones: a) |x-2| = |x-6| b) |1/x| = |x-4|

2. Calcula el dominio de las siguientes funciones:

; ;

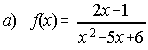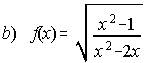; ; f) f(x)= tagx

3. Calcula los siguientes límites:

; ;

; ; ; ;

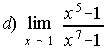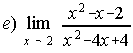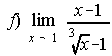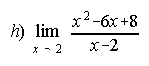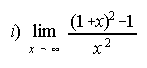
4. ¿Tiene límite la función 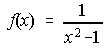en x=1?. ¿ Y ?.

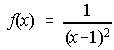5. Estudia la continuidad de las funciones siguientes:

;

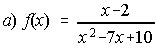6. Representa gráficamente las siguientes funciones y halla los puntos de discontinuidad que presenten:

; ;

;

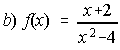7. Calcula "a" para que sea continua.

8. Determina a y b para que la función f(x) sea continua.

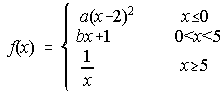
9. Dada la función f(x), halla a y b para que sea continua y dibuja su gráfica.

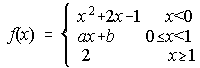
10. Dada la función f(x), se pide: a) Dibuja la gráfica de f.

b) Clasifica sus puntos de discontinuidad.

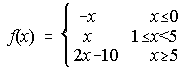
11. Estudia la continuidad de la función

12. Estudia la continuidad de la función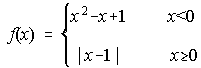

13. Siendo la función f(x), halla "b" para que sea continua en x=pi.

14. Dada la función f(x), estudia para que valores de "a" puede definirse f(1) resultando así una función continua.

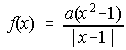
15. La función f(x) no está definida en x=1. Halla "a" para que sea posible definir f(1) resultando así una función continua.

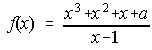
16. La función f(x) es discontinua en x=2. Calcula "b" y clasifica todas sus discontinuidades.

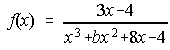
17. Halla k para que la función f(x) sea continua.

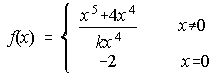
18. Calcula "a" para que sean continuas las funciones siguientes:

; ;

19. Halla "k" para que la función f(x) tenga en x=2 una discontinuidad evitable.

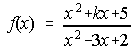
20. Halla "a" y "b" para que la función f(x) sea continua.

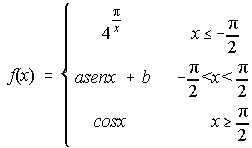
21. La función f(x): a) ¿es continua en [0,1]? ¿Por qué?

b) Halla una cota superior y otra inferior en [0,1]. c) Halla su máximo y su mínimo en [0,1].

22. Estudia la continuidad de la función f(x). Estudia si se verifica el teorema de Bolzano en el intervalo [-1, 5 pi/4]. En caso afirmativo halla los puntos en los que se verifica la tesis de dicho teorema.

23. Calcula "b" para que la función f(x) sea continua. Comprueba si se cumple el teorema de Bolzano en el intervalo [0,3].

24. Demuestra que la ecuación x = cosx tiene una solución en el intervalo (0,1).

25. Demuestra que las siguientes ecuaciones tienen alguna solución real:

a) 2 - x = Lnx ; b) x = 3 + senx ; c) e^-x = x - 2

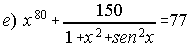
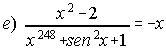
26. Averigua si la función f(x)= x³-5x+4 tiene algún cero negativo.

27. La función f(x) toma signo distinto en los extremos del intervalo [2,4]. ¿Se anula en algún punto de ese intervalo? ¿Contradice el teorema de Bolzano? La misma pregunta para f(x)= tagx en [0,pi].

28. Podemos aplicar el teorema de Bolzano para asegurar que la ecuación siguiente: tiene alguna solución en el intervalo (0,3), ¿y en el intervalo (-2,0)? Razona la respuesta.

29. Sea f(x)= x³-x²+x. Demuestra que existe al menos un punto a en el intervalo (1,2), tal que f(a)= 2'2361.

30. Determina los valores del número K para los que la función f(x)=x³-3x+K se anule en algún punto del intervalo [-1,1].

31. Sean f y g dos funciones continuas en [a,b] tales que f(a) < g(a) y f(b) > g(b). Prueba que f(c)=g(c) para algún número c en (a,b).

32. Si f(x) es continua en [1,9] y es tal que f(1)=-5 y f(9)>0 , ¿podemos asegurar en estas condiciones que la función definida como g(x)= f(x)+3 tiene al menos un cero en el intervalo [1,9].

33. Si f(x) es continua en [a,b] siendo c y d pertenecientes al intervalo [a,b] en los que f(c)=10 y f(d)=7. Demuestra que la función g(x)=f(x)+7 es tal que existe p de (a,b) con g(p)=15.

34. Si f(x) es continua en [5,8] y además f(5)=1 y f(8)=3, entonces:

a) Todos los valores de f(x) están en el intervalo [1,3].

b) Existe un x en [5,8] tal que f(x)= 1'4142. c) Se verifica siempre que f(x)>1 en este intervalo.

Razona la respuesta correcta.

35. Se dice que una raíz de una ecuación está separada cuando se ha encontrado un intervalo en el que la ecuación tiene esa raíz y esa sola. Separa las 4 raíces de la ecuación: 2x⁴-14x²+14x-1=0.

SOLUCIONES

1. a) x=4 ; b) x=2 ±2'2361 , x=2±1'7321

2. a) (-inf,2)u(2,3)u(3,+inf) ; b) (-inf,-1]u(0,1]u(2,+inf) ; c) (-inf,-4]u[4,+inf)

d) (-inf,-2)u(2,+inf) ; e) R ; f) R-{múltiplos impares de pi/2}

3. a) -inf ; b) 0 ; c)-1/16 ; d) 5/7 ; e) ±inf ; f) 3 ; g) -1/2 ; h)-2 ; i) 1

4. No . Si.

5. a) En x=2 discontinuidad evitable y en x=5 discontinuidad de salto infinito.

b) Discontinuidad de salto finito en x=0.

6. a) x=0 discontinuidad de salto infinito.

b) Discontinuidad evitable en x=-2 y de salto infinito en x=2.

c) y d) x=0 discontinuidad de salto finito. e) Continua en R .

7. a=1 . . . . . . . . 8. a=1/4 , b=-1/25 . . . . . . . 9. a=3, b=-1

10. x=0 continua por la izquierda. En x=1 continua por la derecha y en x=5 discontinua de salto finito.

11. x=3 discontinuidad infinita. . . . . . . . . . . 12. Continua en R.. . . . . . . . 13. b= - 2pi

14. a=0 pero entonces f(x)=0. . . . . . . . . . . 15. a=-3

16. b=-5 y en x=1 y x=2 discontinua de salto infinito. . . . . . . . 17. k=-2

18. a) a=-8 ; b) a=1/2 ; c) a= ½ . . . . . . . 19. K=-9/2 . . . . . . . 20. a=-1/32 , b=1/32

21. a) mínimo y cota superior x=0. Máximo y cota inferior en x=1.

22. x=-2 discontinuidad de salto finito. Si c= 0 y c=pi.

23. b= -7/4 . No. . . . . . . . . . . Del 24. al 29. Aplicar el teorema de Bolzano.

30. k de [-2,2] . . . . . . . . . 32. Si. . . . . . . . 34. a) Falsa , b) Verdadera , c) Falsa.

35. [-4,-3] , [0,1] , [1,1'5] y [1'5,2]