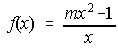
-- DERIVADAS --

1. Aplicando la definición de derivada, halla m para que f'(1)=0 en la función siguiente:

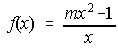
2. Calcula la derivada de las siguientes funciones y expresa el resultado de la forma más simple posible:

; . . . ; . . .

; . . . . ; . . . .

; . . . . ; . . . .

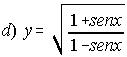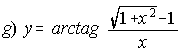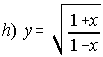3. Estudia la continuidad y derivabilidad de las siguientes funciones:

; . . . . .

; . . . . . . . . . . . . . . . . . .

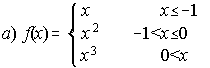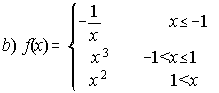
4. La función f(x)= x + 1 no es derivable en un punto. ¿Cuál es?. Representa la función y razona la respuesta.

5. La función f(x)= x² - 6x + 8 no es derivable en dos puntos. ¿Cuáles son ?. Representa la función y razona la respuesta.

6. Halla la ecuación de la tangente y la normal a la parábola de ecuación y= x² + x + 1 en el punto de abscisa x=2.

7. Halla la ecuación de la recta tangente a en el punto de abscisa x=0.

8. Obtén los puntos de la gráfica de f(x)= x⁴ - 7x³ +13x² + 3x + 4 en los que la tangente es paralela a y -3x -2 =0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 1990)

9. Obtén la ecuación de la recta tangente y normal a la curva en el punto P(2,3).

10. Dada la función f(x)= x|x|, estudia la existencia de su primera y segunda derivada.

11. En el trozo de la parábola y= x² comprendido entre los puntos A(1.1) y B(3,9), halla un punto cuya tangente sea paralela a la cuerda AB.

12. Calcula los siguientes límites:

; . . . . . . . . . . . . . ; . . . . . . . . .

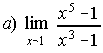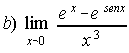(Ju.89) ; . . . . . . (Ju.90)

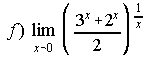(Sep. 91) ; . . . . . . 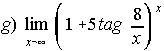(Ju.93)

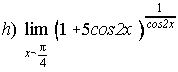(Sep. 93) ; . . . . . .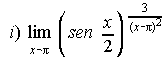

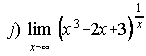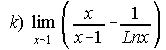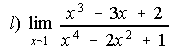; . ; . . (Prop. 2.001)

13. Prueba que la ecuación x⁵-5x-1=0 tiene exactamente tres raíces reales.

14. Prueba que la ecuación x³+6x²+15x-23=0 tiene una única raíz real.

15. Prueba que x¹⁸-5x+3=0 tiene como máximo dos raíces reales.

16. Estudia la continuidad y derivabilidad de las siguientes funciones:

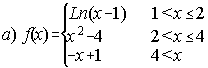(Sep. 92) ; . . . . . 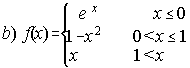(Ju. 93)

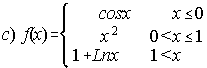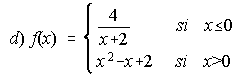; . . . . . . . (Prop. 2.001)

17. Dada la función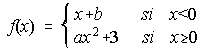 determina, "a" y "b" para que f(x) sea continua y no derivable en x=0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Prop. 2.001)

SOLUCIONES

1. m=-1

3. a) x=-1 discontinua y x=0 continua y derivable.

b) x=-1 discontinua, x=1 continua y no derivable.

c) Continua y derivable en R.

d) Continua en R, no derivable en x=0.

4. x=-1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5. x=2 y x=4

6. Recta tangente: 5x-y-3=0 ; Recta normal: x+5y-37=0

7. Recta tangente: y=3 . . . . . . . . . . . . . . . . . . . . . 8. x=0, x=2, x=13/4

9. Recta tangente: y =3 ; Recta normal: x=2

10. La primera derivada existe en todo R y la segunda no existe en x=0.

11. (2,4)

12. a) 5/3 ; b) 1/6 ; c)1 ; d) 1 ; e) e^-6 ; f) 2.44948 ; g) e^{40 ;} h) e^{5 ;} i) e^-3/8 ; j) 1 ; k) ½ ; l) 3/4.

16. a) En x=2 continua y no derivable. En x=4 discontinua.

b) En x=0 es continua y no derivable y en x=1 discontinua.

c) En x=0 no es continua y en x=1 continua y no derivable.

d) No es continua ni derivable en x=-2.

17. Es continua y no derivable para b=3 y a cualquier número.